【数据结构练习】树和二叉树的选择题精选集锦

前言

编程想要学的好，刷题少不了，我们不仅要多刷题，还要刷好题！为此我开启了一个弯道超车必做好题锦集的系列，此为树和二叉树的选择题精选集锦。该系列会不定期更新，敬请期待！

1.已知某二叉树的中序遍历序列为JGDHKBAELIMCF，后序遍历序列为JGKHDBLMIEFCA，则其前序遍历序列为（）

A.ABDGHJKCEFILM

B.ABDGJHKCEILMF

C.ABDHKGJCEILMF

D.ABDGJHKCEIMLF

答案：B

解析：

由后序遍历确定子树的根，后序遍历从后向前看，最后一个元素为根，和前序遍历刚好相反，从后向前看后序遍历，应该是根，右，左，根据中序遍历确定子树的左右区间

故：根为: A

A的左子树：JGDHKB       A的右子树：ELIMCF

A的左子树的根：B        A的右子树的根：C

B的左子树：JGDHK  B的右子树：空  C的左子树：ELIM C的右子树：F

B的左子树的根：D         C的左子树根：E

D的左子树的根：G D的右子树的根：H  E的右子树的根:I

故树的结构为：

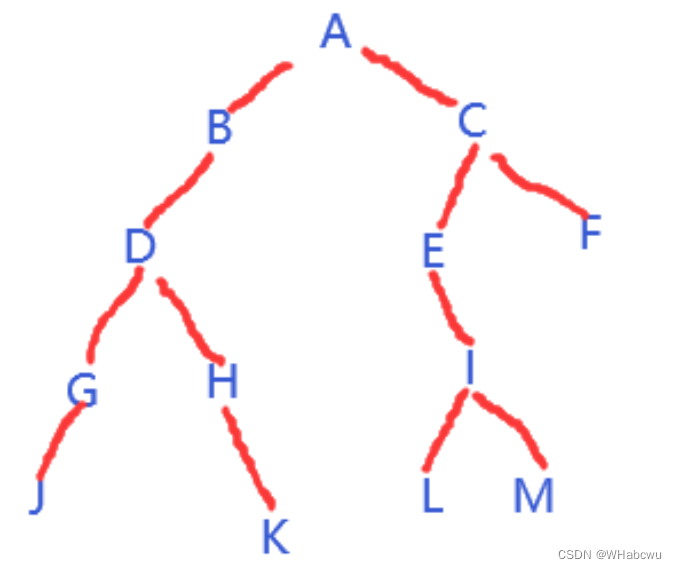
2.设根结点的深度为1，则一个拥有n个结点的二叉树的深度一定在（）区间内

A.[log(n + 1)，n]

B.[logn，n]

C.[log(n + 1)，n - 1]

D.[log(n + 1)，n + 1]

答案：A

解析：

最大深度：即每次只有一个节点，次数二叉树的高度为n，为最高的高度

最小深度：此树为完全二叉树，如果是完全二叉树

根据二叉树性质，完全二叉树的高低为 h = log(n+1)向上取整

故选择A

3.二叉树的( )遍历相当于广度优先遍历，( )遍历相当于深度优先遍历

A.前序中序

B.中序前序

C.层序后序

D.层序前序

答案：D

解析：

广度优先需要把下一步所有可能的位置全部遍历完，才会进行更深层次的遍历，层序遍历就是一种广度优先遍历。

深度优先是先遍历完一条完整的路径（从根到叶子的完整路径），才会向上层折返，再去遍历下一个路径，前序遍历就是一种深度优先遍历。

4.如果一颗二叉树的前序遍历的结果是ABCD，则满足条件的不同的二叉树有（）种

A.13

B.14

C.15

D.16

答案：B

解析：

首先这棵二叉树的高度一定在3~4层之间:

三层：

四层：

如果为四层，就是单边树，每一层只有一个节点，除过根节点，其他节点都有两种选择，在上层节点的左边还是右边，所以2*2*2共8种

总共为14种。

4.n个节点的完全二叉树，最多可以有多少层？

A.n/2

B.log(n)+1(向下取整)

C.n-1

D.n

解析：

根据二叉树性质4：对于完全二叉树，节点个数为n时高度h为

h = log(n+1)向上取整或者即3.x 取4

h = log(n)+1向下取整即3.x 取 3

故应该选择B

5.设一棵二叉树中有3个叶子结点，有8个度为1的结点，则该二叉树中总的结点数为（）个

A.11

B.12

C.13

D.14

答案：C

解析：

设Ni表示度为i的节点个数，则节点总数 N = N0 + N1 + N2

节点个数于节点边的关系： N个节点的树有N-1个边

边与度的关系：N - 1 = N1 + 2 * N2

故：N0 + N1 + N2 - 1 = N1 + 2 * N2

因此，得：N0 = N2 + 1

回到原题，N0 = 3，N1 = 8，可得N2 = 2。

因此答案是 3 + 8 + 2 = 13。

6.一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反，则该二叉树一定满足（）

A.所有的结点均无左孩子

B.所有的结点均无右孩子

C.只有一个叶子结点

D.至多只有一个结点

答案：C

解析：

前序遍历：根左右

后序遍历：左右根

从二叉树前序和后序遍历结果规则中可以看出，如果树中每个节点只有一个孩子时，遍历结果肯定是反的

比如下面这前序和中序序列所构成的树的结构:

12345

54321

故每个节点只有一个孩子，即只有一个叶子节点

7.在一颗度为3的树中，度为3的结点有2个，度为2的结点有1个，度为1的结点有2个，则叶子结点有（）个

A.4 B.5 C.6 D.7

答案：C

解析：

设度为i的节点个数为ni, 该树总共有n个节点,则n=n0+n1+n2+n3.

有n个节点的树的总边数为n-1条.

根据度的定义,总边数与度之间的关系为：n-1=0*n0+1*n1+2*n2+3*n3.

联立两个方程求解,可以得到n0 = n2 + 2n3 + 1, n0=6

8.一颗拥有1000个结点的树度为4，则它的最小深度是（）

A.5 B.6 C.7 D.8

答案：B

解析：

如果这棵树每一层都是满的，则它的深度最小，假设它为一个四叉树，高度为h，则这个数的节点个数为(4^h - 1) / 3，当h = 5, 最大节点数为341，当h = 6, 最大节点数为1365，所以最小深度应该为6。

9.一颗完全二叉树有1001个结点，其叶子结点的个数是（）

A.251 B.500 C.501 D.不能确定

答案：C

解析：

该题需要用到二叉树性质：在任意二叉树中，度为0的节点都比度为2的节点多1个，即 n0 = n2 + 1

另外，在完全二叉树中，如果节点总个数为奇数，则没有度为1的节点，如果节点总个数为偶数，只有一个度为1的节点

因此：n0 + n1 + n2 = 1001 节点总数为奇数，没有度为1的节点

n0 + 0 + n2 = 2*n0-1 = 1001 n0 = 501

以上为我个人的小分享，如有问题，欢迎讨论！！！

都看到这了，不如关注一下，给个免费的赞