一、一些概念

1. 排序方法是“稳定的”：假设两个元素相等，若在排序后的序列中，排序前就在前面的元素仍在前面，则称所用的排序方法是稳定的；反之，若排序后两个相等元素调换相对位置，则称所用的排序方法是不稳定的

二、分类

1. 按排序过程中的原则：
   • 插入排序
   • 交换排序
   • 选择排序
   • 归并排序
   • 计数排序
2. 按内部排序过程中所需的工作量：
   • 简单的排序算法：时间复杂度为$O(n^2)$
   • 先进的排序算法：时间复杂度为$O(nlogn)$
   • 基数排序：时间复杂度为$O(d\cdot n)$

三、一些准备工作

待排记录的数据类型设为：

#define MAXSIZE 20 // 一个用作示例的小顺序表的最大长度
typedef int KeyType;  // 定义关键字类型为整数类型
typedef struct {KeyType key;  // 关键字项InfoType otherinfo;  // 其他数据项
} RedType;  // 记录类型typedef struct {RedType r[MAXSIZE+1];  // r[0]闲置或用作哨兵单元int length;  // 顺序表长度
} SqList;  // 顺序表类型

四、插入排序

每次将一个待排序的记录按其关键字大小插入到前面已排好序的子序列中

1. 直接插入排序：将一个记录插入到已排好序的有序表中，从而得到一个新的、记录数增1的有序表
   • 一趟直接插入排序：一趟会将一个记录插入有序表，有序表的记录数+1.
   • 整个排序过程为n-1趟插入
   • 算法分析

     void InsertSort(SqList &L){for (int i=2; i<L.length; ++i)if (L.r[i].key<L.r[i-1].key){L.r[0] = L.r[i];L.r[i] = L.r[i-1];for (j=i-2; L.r[0].key<L.r[j].key; --j)L.r[j+1] = L.r[j];  // 记录后移L.r[j+1] = L.r[0];  // 将当前元素插入到正确位置}
     }
     

2. 折半插入排序：由于插入排序的基本操作是在一个有序表中进行查找和插入，因此这个“查找”操作可利用“折半查找”来实现

void BInsertSort(SqList &L){for (i=2; i<L.length; ++i){L.r[0] = L.r[i];low = 1; high = i - 1;while (low<=high){m = (low+high) / 2;if (L.r[0].key<L.r[m].key)  high = m-1;  // 插入点在低半区else low = m+1;  // 插入点在高半区}for (j=i-1; j>=high+1; --j)  L.r[j+1] = L.r[j];  // 记录后移L.r[high+1] = L.r[0];  // 插入}
}

3. 希尔排序：又称缩小增量排序，也是一种插入排序类的算法，但时间效率较上述有较大改进
   • 思想：对于直接插入排序，若待排序列原本就为正序，其时间复杂度可提高为$O(n)$，由此可知若待排序序列关键字基本有序，则直接插入排序的效率可大大提高
   • 原理：先将整个待排序列分割成若干子序列，分别进行直接插入排序，由此可让整个序列中的记录“基本有序”，此时再对全体记录进行一次直接插入排序。这样一来，前后记录位置的增量是dk而不是1

五、交换排序

根据序列中两个关键字的比较结果来对换这两个记录在序列中的位置

1. 起泡排序：
   • 一趟排序：先比较第一个和第二个，若为逆序则交换；再比较第二个和第三个，以此类推，直至第n-1个和第n个记录的关键字对比完为止。这称为第一趟起泡排序
   • 第i趟排序会使关键字第i大的记录被安置到正确的位置上
   • 判别起泡排序结束的条件：在一趟排序过程中没有进行过交换记录的操作
2. 快速排序：通过一趟排序将待排序列分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，然后分别对这两部分继续进行排序，以达到整个序列有序
   • 一趟排序：任意选一个记录作为枢轴pivotkey，将所有小于它的记录都放在它之前，所有大于它的都放在它之后。具体做法是：附设两个指针low和high，首先从high所指位置起向前搜索找到第一个小于pivotkey的记录放到low位置上，然后从low下一个位置起向后搜索找到第一个大于pivotkey的记录放到high位置上。重复这两步直到low=high为止
   • 一趟排序结束会将枢轴放到正确位置上（即最后high=low的位置处）
   • 当初始序列有序/逆序或基本有序/逆序时，快速排序会退化为起泡排序

六、选择排序

每一趟在待排序元素中，选取关键字最小（或最大）的元素加入有序子序列

1. 简单选择排序：
   • 第i趟排序：通过n-i次关键字间的比较，从n-i+1个记录中选出关键字最小的记录，并和第i个记录交换
   • 简单选择排序中，所需进行记录移动的次数比较少（因为只是比较+给min的下标赋值），而无论记录的初始排列如何，所需进行的关键字间的比较次数相同
2. 堆排序：
   • 堆的定义：n个元素的序列$k_1,k_2,...,k_n$当且仅当满足下关系时，称之为堆：
     
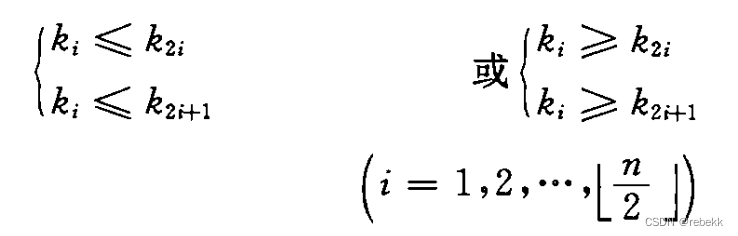
   • 堆排序要解决两个问题：1）如何由一个无序序列建成一个堆；2）如何在输出堆顶元素后，调整剩余元素成为一个新的堆
     • 2）堆顶元素和堆底元素互换（即输出堆顶元素，然后以堆底元素替换之），然后自上而下进行调整即可，称这个“自堆顶至叶子”的调整过程为“筛选”
     • 1）从一个无序序列建堆的过程就是一个反复“筛选”的过程。且只需要从第$\lfloor \frac{n}{2}\rfloor$ 个元素开始，依次往前筛选即可
   • 堆排序方法对于记录数较少的文件并不提倡，而对于n较大的文件还是很有效的。因为其运行时间主要耗费在建初始堆和调整新堆时进行的反复“筛选”上（即代码中的HeadAdjust）。对深度为k的堆，筛选算法中进行的关键字比较次数至多为2(k-1)次
   • 堆排序在最坏的情况下，其时间复杂度也为$O(nlogn)$，且仅需一个记录大小供交换用的辅助存储空间

外部排序

1. 外部排序基本上由两个相对独立的阶段组成：
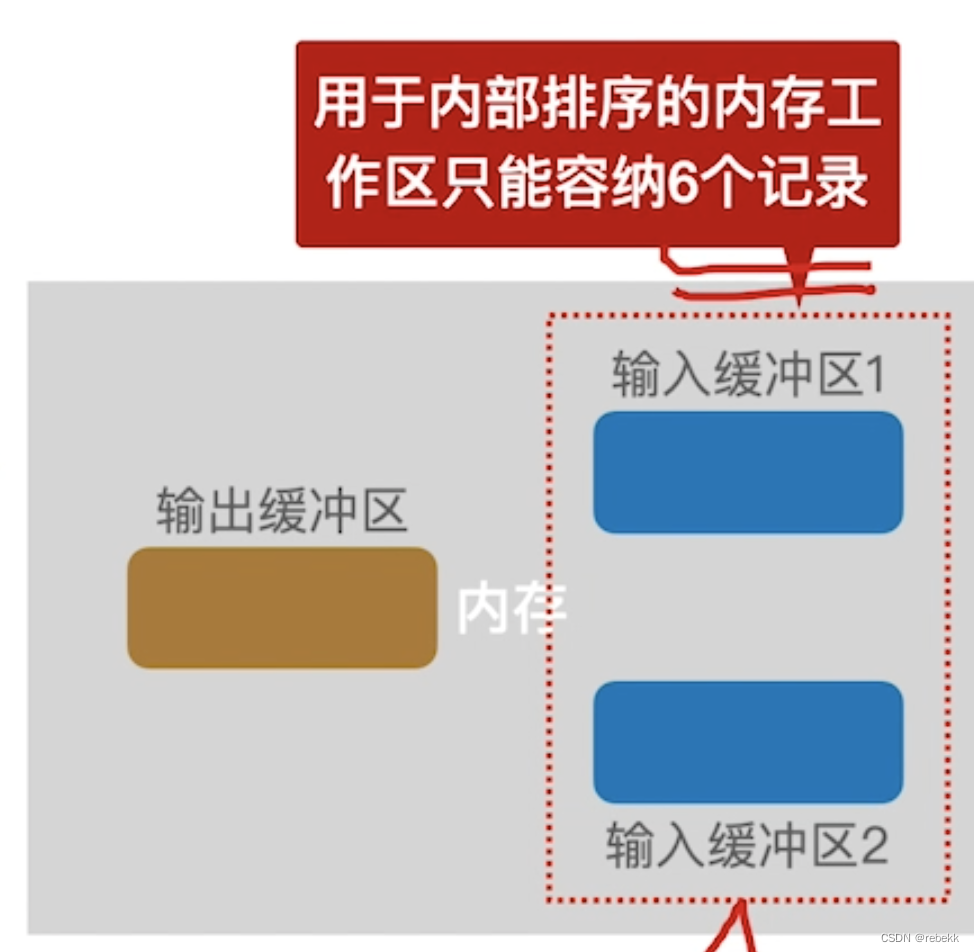
   • （初始）归并段：按照可用内存大小，将外存上含n个记录的文件分成若干长度为l的子文件或段，依次读入内存并利用有效的内部排序方法对每个子文件各自进行排序，并将排序后得到的有序子文件重新写入外存，通常称这些有序子文件为归并段或顺串（这一阶段是内部排序的内容，就是逐个段读入内存，然后直接内部排序，最后再写回外存。若用于内部排序的内存工作区能容纳$l$个记录，则初始归并段中就包含$l$个记录，如下图）
     
   • 然后对这些归并段进行逐趟归并，使归并段（有序的子文件）逐渐由小至大，直至得到整个有序文件为止（这一阶段是外部排序主要探讨的问题，也就是归并的过程）
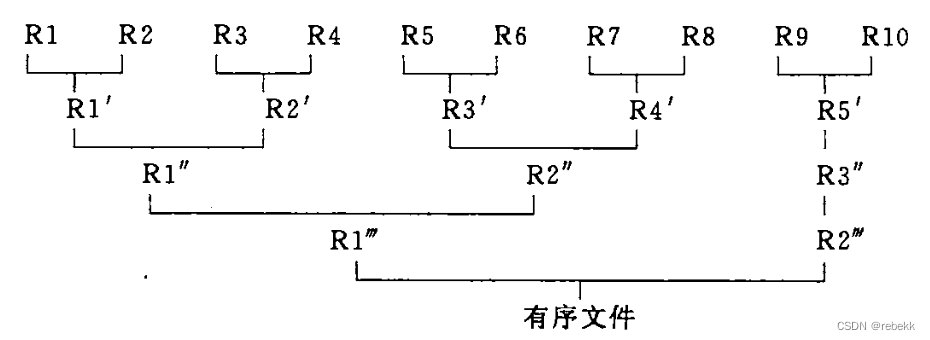
2. 一个2-路平衡归并的具体例子：假设有一个含10000个记录的文件
   • 首先通过10次内部排序得到10个初始归并段，每一段都含有1000个记录
   • 然后对这些初始归并段两两作归并
   • 然后对第一次归并得到的5个归并段再两两归并
   • 然后对第二次归并得到的3个归并段再两两归并
   • 然后对第四次归并得到的2个归并段再两两归并，得到有序文件
     
3. 外部排序的特点
   • 在外部排序中实现两两归并时，不仅要调用merge过程，而且要进行外存的读/写，因为不可能将两个有序段（归并段）及归并结果段同时存放在内存中。假设每个物理块可容纳200个记录（$50\times 200=10000$），则每趟归并需要进行50次读和50次写，生成初始归并段+4趟归并就需要500次读写（$100+100\times 4$)
   • 外部排序所需时间=内部排序（产生初始归并段）所需时间+外存信息读写时间+内部归并所需时间
     • 这其中，外存信息读写时间明显占时间大头，因此，提高外排的效率应主要着眼于减少外存信息读写的次数。而对于同一文件，这个读写次数和归并的趟数成正比，一般情况下，对m个初始归并段进行k-路平衡归并时，归并的趟数$s=\lfloor lo{g}_{k}m\rfloor$，可见若增加k或减少m，就能减少s
4. 提高外部排序效率/减少外存信息读写时间/减少归并趟数：
   • 增加k：对于k个归并段一起归并，归并结果中的第一个记录就是k个归并段中关键字最小的记录，则得到归并结果中的每一个记录，都需要进行k-1次比较。因此随着k的增长，内部归并时间也增长，这将抵消由于增大k而减少外存信息读写时间所得效益。
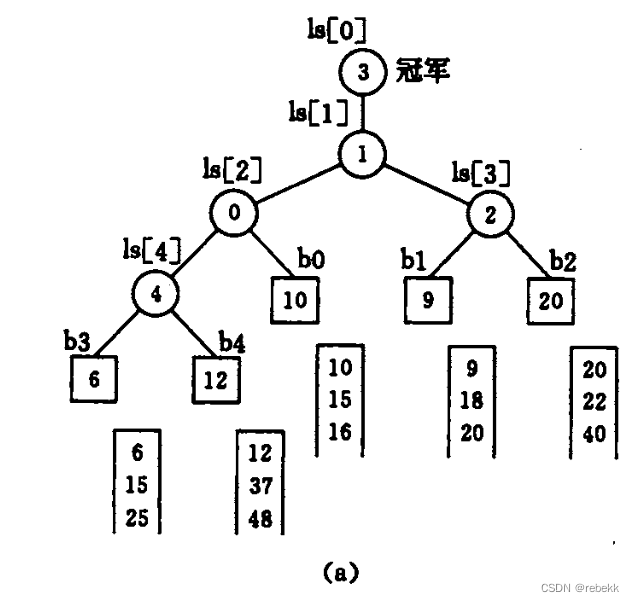
     • 败者树：使得在k个记录中选出关键字最小的记录时仅需进行$\lfloor lo{g}_{2}k\rfloor$次比较，从而使总的内部归并时间减少。（之前从k个记录选择一个最小的需要k-1次）。
     • 败者树是一个完全二叉树，k个叶节点分别对应k个归并段中当前参加比较的元素，非叶子节点用来记忆左右子树中的失败者，而让胜者往上继续比较，一直到根节点
     • 如下图，方形节点表示叶子节点（或外节点），分别为5个归并段中当前参加归并的记录的关键字；根节点ls[1]的双亲节点ls[0]为冠军（最小关键字记录）；节点ls[3]指示b1和b2两个叶子节点中的败者即b2，而胜者b1和b3进行比较，节点ls[1]指示它们中的败者为b1。在选择最小关键字的记录之后，只要修改叶子节点b3中的值，使其为同一归并段中的下一个记录的关键字，然后从该节点向上和双亲节点所指的关键字进行比较，败者留在该双亲节点，胜者继续向上直至树根的双亲。
       
   • 减少m：m是外部文件经过内部排序之后得到的初始归并段的个数，$m=\lceil \frac{n}{l}\rceil$（$n$为外部文件中的记录数，$l$为初始归并段中的记录数）。$l$的大小完全依赖于进行内部排序时可用内存工作区的大小。
     • 置换选择排序：FI为初始待排文件，FO为初始归并段文件，WA为内存工作区，FO和WA的初始状态为空，并设内存工作区WA的容量可容纳$w$个记录，MINIMAX记录为从WA中选出的最小的记录
       • 在WA中选择MINIMAX记录的过程是利用败者树来实现的：WA中的记录作为败者树的外部节点，而败者树中根节点的双亲节点指示工作区中关键字最小的记录。
       • 由置换选择排序所得初始归并段的长度不等
       • 若不计输入、输出的时间，则对n个记录的文件而言，生成所有初始归并段所需时间为$O(nlogw)$
   • 最佳归并树：由置换-选择生成所得的m个初始归并段，构造一棵哈夫曼树作为归并树，即可使在进行外部归并时所需对外存进行的读/写次数达最少。当初始归并段的数目不足时，需附加长度为0的“虚段”
     • 对于k-路归并，m个初始归并段，若$(m-1)MOD(k-1)=0$，则不需要加虚段，否则需要附加$k-(m-1)MOD(k-1)-1$个虚段，即，第一次归并为$(m-1)MOD(k-1)+1$路归并