【数据结构】论如何拿捏快速排序？（含非递归）

目录

一，快速排序（递归）

1，快排思想

2，霍尔排序

3，挖坑法

4，前后指针法

5，快速排序优化

1，三数取中法选key

2，小区间优化

二，快速排序（非递归）

Stack.h

Stack.c

三，快速排序源代码

一，快速排序（递归）

1，快排思想

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止；

基本代码思想如下： 

// 假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int array[], int left, int right)
{if(right < left)return;// 按照基准值对array数组的 [left, right)区间中的元素进行划分int div = partion(array, left, right);// 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)// 递归排[left, div)QuickSort(array, left, div);// 递归排[div+1, right)QuickSort(array, div+1, right);
}

上述为快速排序递归实现的主框架，发现与二叉树前序遍历规则非常像，同学们在写递归框架时可想想二叉树前序遍历规则即可快速写出来，后序只需分析如何按照基准值来对区间中数据进行划分的方式即可；

2，霍尔排序

根据快排思想，我们需要实现的就是 partion 函数了----将区间按照基准值划分为左右两半部分；

常见的方式有很多，我们先来了解最初的版本 【霍尔排序】

思想图解：

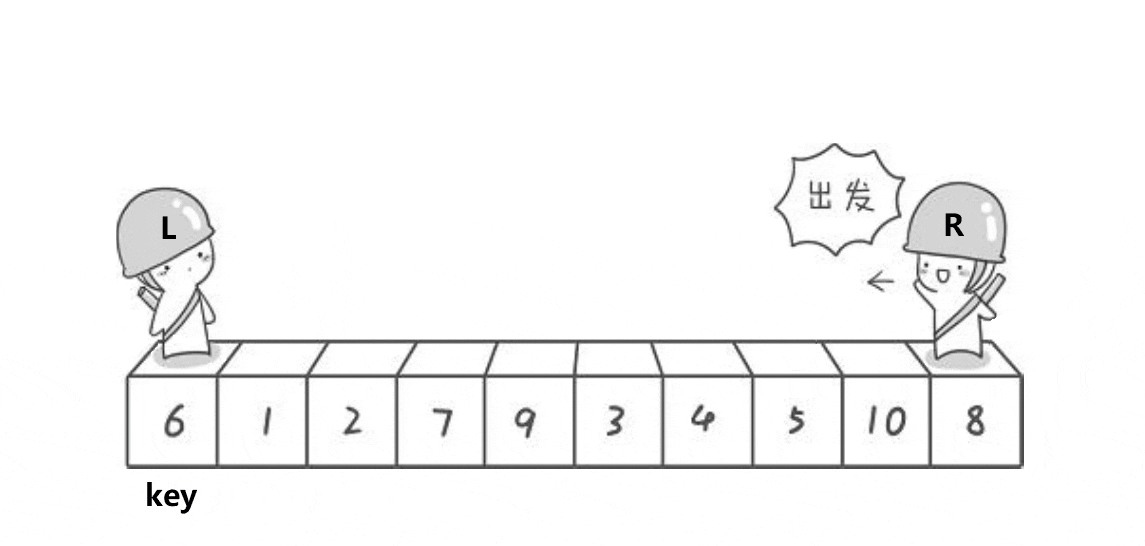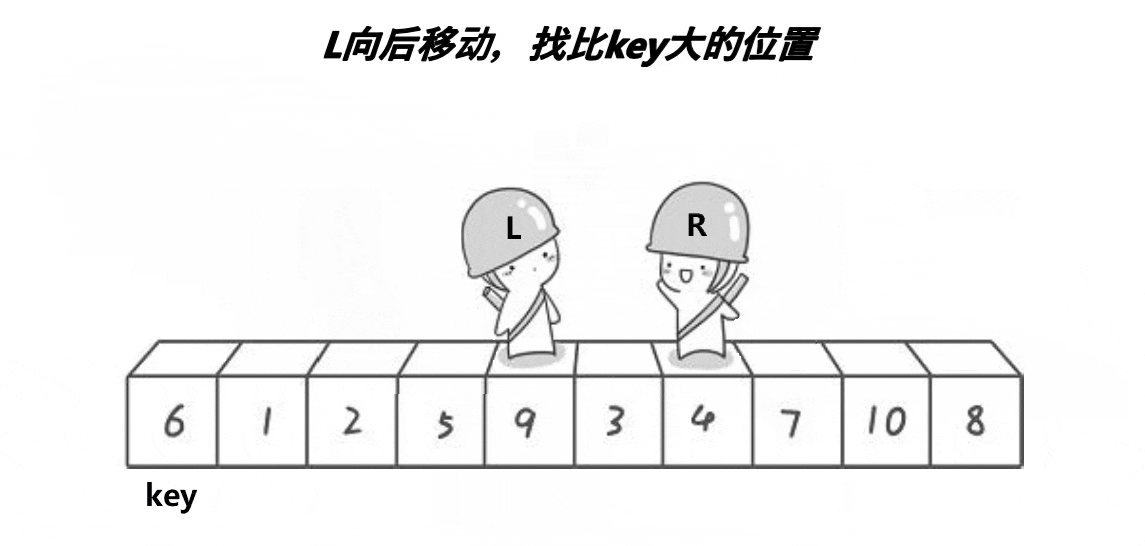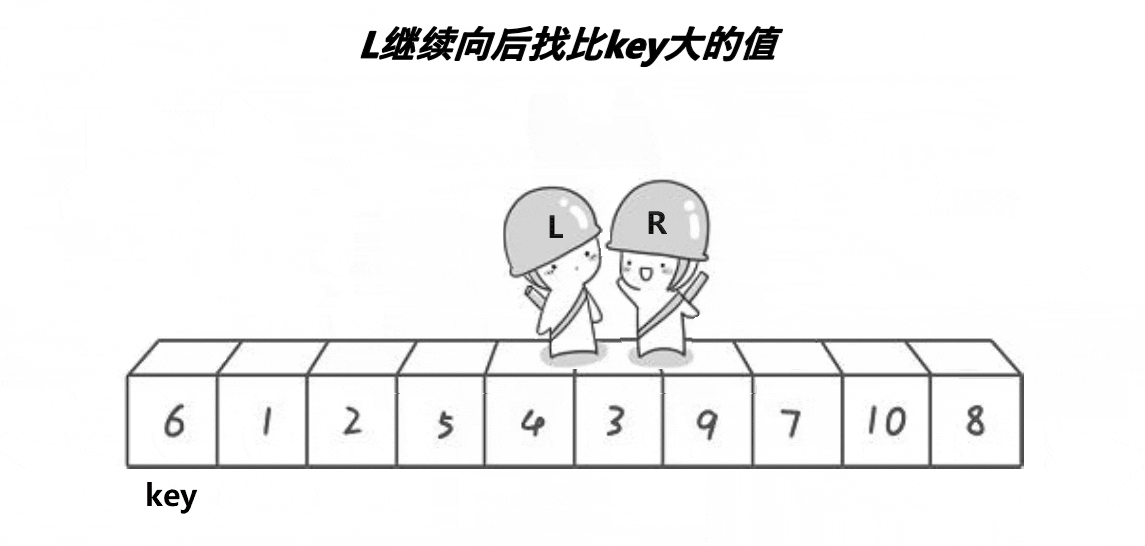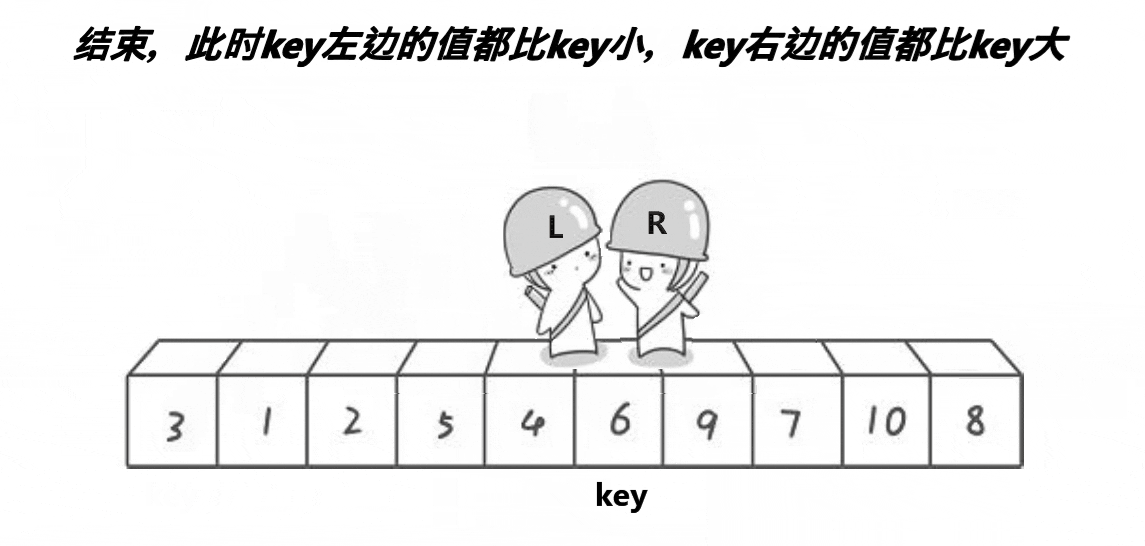
对就是这样的，右边的小人先出发向左移动，找到比 key 小的数，然后左边的小人向右移动找到比  key 大的数，然后交换两个小人的值，直至他们相遇然后再交换 key 与任意一个小人的值；

这样一趟下来，他们相遇后，左边的数都比 key 小，右边的数都比 key 大；

思路实现：

//霍尔排序
int PartSort1(int* arr, int left, int right)
{int keyi = left;while (left < right){//右边先走while (left<right && arr[right]>=arr[keyi]){right--;}//左边后走while (left < right && arr[left] <= arr[keyi]){left++;}//交换Swap(&arr[left], &arr[right]);}Swap(&arr[left], &arr[keyi]);return left;
}

然后我们运行一下：

//快速排序
void QuickSort(int* arr, int begin, int end)
{if (begin >= end){return NULL;}//霍尔法int keyi = PartSort1(arr, begin, end);//排序[begin,keyi) & [keyi+1,end]QuickSort(arr, begin, keyi);QuickSort(arr, keyi + 1, end);
}int main()
{int arr[] = { 9,1,2,5,7,4,8,6,3,5 };//快速排序QuickSort(arr, 0,sizeof(arr) / sizeof(arr[0])-1);PrintSort(arr, sizeof(arr) / sizeof(arr[0]));return 0;
}

可以看到是有序的，选择排序就 OK 了；

3，挖坑法

然后我们再来认识另一种方式 【挖坑法】，其实跟【霍尔排序】思路差不多，不过更容易理解一点；

思想图解:

对还是一样的思路，让第一个元素为坑位，然后右边的小人先出发向左走找比 key 小的数，然后填充坑位并且右边小人的位置变为新坑位，然后左边的小人向右走找比 key 大的数，然后填充坑位并且左边小人的位置变为新坑位，直至两个小人相遇于坑位然后再给坑位赋值 key ；

这样一趟下来，坑位左边的数都比 key 小，右边的数都比 key 大；

思路实现：

//挖坑法
int PartSort2(int* arr, int left, int right)
{int key = arr[left];//坑位int hole = left;while (left < right){//右边找小while (left < right && arr[right] >= key){right--;}arr[hole] = arr[right];hole = right;//左边找大while (left < right && arr[left] <= key){left++;}arr[hole] = arr[left];hole = left;}arr[hole] = key;return hole;
}

然后我们运行一下：

//快速排序
void QuickSort(int* arr, int begin, int end)
{if (begin >= end){return NULL;}//挖坑法int keyi = PartSort2(arr, begin, end);//排序[begin,keyi) & [keyi+1,end]QuickSort(arr, begin, keyi);QuickSort(arr, keyi + 1, end);
}

可以看到是有序的，选择排序就 OK 了；

4，前后指针法

然后呢，在介绍最后一种排序方式了 【前后指针】法；

这个呢就比较新颖了，跟之前的都不一样；

请看图解：

这个呢就是，定义两个指针，从首元素开始走，快指针（cur）刚开始领先慢指针（prev）一个身位，然后 cur 先走找比 key 小的数，然后与 prev 的下一个数交换，直至 cur 越界，然后再让 prev 与 key 交换；

这样一趟下来，prev 左边的数都比 key 小，右边的数都比 key 大；

 思路实现：

//前后指针法
int PartSort3(int* arr, int left, int right)
{int keyi = left;int slow = left, fast = left+1;while (fast<=right){if (arr[fast] < arr[keyi] && ++slow!=fast){//交换Swap(&arr[fast], &arr[slow]);}fast++;}Swap(&arr[slow], &arr[keyi]);return slow;
}

然后我们运行一下：

//快速排序
void QuickSort(int* arr, int begin, int end)
{if (begin >= end){return NULL;}int keyi = PartSort3(arr, begin, end);//排序[begin,keyi) & [keyi+1,end]QuickSort(arr, begin, keyi);QuickSort(arr, keyi + 1, end);
}

可以看到是有序的，选择排序就 OK 了；

5，快速排序优化

1，三数取中法选key

这第一个呢，就是对 key 的取值进行优化，当 key 的值太过于小或者大时，遍历数组的时间会增加，所以我们尽量让 key 的取值随机；

我们可以取首元素，尾元素，中间元素的值进行比较选 key ；

思路实现：

//三数取中
int middle(int* arr, int left, int right)
{//int mid = (left +right)/ 2;if (arr[left] < arr[mid]){if (arr[mid] < arr[right]){return mid;}if (arr[left] < arr[right]){return right;}else{return left;}}//arr[mid]<=arr[left]else{if (arr[mid] > arr[right]){return mid;}if (arr[left] > arr[right]){return right;}else{return left;}}
}

这样我们选择的 key 就不会受 首元素的束缚了；

我们还可不可以在这个基础上再优化一下呢？

答案是肯定的！

我们可以用随机数来取代中间数；

//三数取中
int middle(int* arr, int left, int right)
{//随机数取中int mid = left + (rand() % (right - left));if (arr[left] < arr[mid]){if (arr[mid] < arr[right]){return mid;}if (arr[left] < arr[right]){return right;}else{return left;}}//arr[mid]<=arr[left]else{if (arr[mid] > arr[right]){return mid;}if (arr[left] > arr[right]){return right;}else{return left;}}
}

这样子才是真正意义上的随机值，这样 key 就不受束缚了，再任何场景下都可以排序自如；

我们选完 key 的下标后，要让数组首元素的值与之交换，这样后面不动就 OK 了；

以【前后指针法】为例：

//前后指针法
int PartSort3(int* arr, int left, int right)
{//三数取中int ret = middle(arr, left, right);Swap(&arr[left], &arr[ret]);int keyi = left;int slow = left, fast = left+1;while (fast<=right){if (arr[fast] < arr[keyi] && ++slow!=fast){//交换Swap(&arr[fast], &arr[slow]);}fast++;}Swap(&arr[slow], &arr[keyi]);return slow;
}

主函数需要写 srand 函数来引用随机值；

//快速排序
void QuickSort(int* arr, int begin, int end)
{srand(time(0));if (begin >= end){return NULL;}int keyi = PartSort3(arr, begin, end);//排序[begin,keyi) & [keyi+1,end]QuickSort(arr, begin, keyi);QuickSort(arr, keyi + 1, end);
}

现在我们运行测试一下：

其实速度是更快的，大家可以在【力扣】上测试一下；

2，小区间优化

还有一种优化方式是当递归到小的子区间时，可以考虑使用插入排序；

当数组的区间不大时，使用【插入排序】是会更快的，同时也可以减少压栈的次数，也就是降低【空间复杂度】；

//快速排序
void QuickSort(int* arr, int begin, int end)
{srand(time(0));if (begin >= end){return NULL;}if (end - begin <10){InsertSort1(arr,begin,end);}else{int keyi = PartSort3(arr, begin, end);//排序[begin,keyi) & [keyi+1,end]QuickSort(arr, begin, keyi);QuickSort(arr, keyi + 1, end);}
}

然后我们还需要改变一下插入排序，之前都是传数组元素个数的，现在我们要传区间需要改造一下；

//插入排序(改造版)
void InsertSort1(int* arr, int left, int right)
{int i = 0;for (i = left; i < right; i++){int end = i;int tmp = arr[end + 1];while (end >= 0){if (arr[end] >= tmp){//交换Swap(&arr[end], &arr[end + 1]);end--;}else{break;}}arr[end + 1] = tmp;}
}

这样就可以了，现在我们运行测试一下：

可以看到是有序的，选择排序就 OK 了；

二，快速排序（非递归）

之前咱们拿捏了递归版的快速排序，现在咱们来秒杀非递归版的快速排序；

我们之前了解到，快速排序与二叉树的前序遍历相似，所以我们非递归也要用这种手法来表示；

所以我们需要借助【栈】来帮助我们来实现；

因为【栈】的特性（后进先出）很符合二叉树的前序遍历的思想，这样我们可以先排序最左边的序列，在排序右边的，前面的都放在【栈】里等后面排序；

所以我们需要一个【栈】：

Stack.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int STDataType;
typedef struct StackTop
{STDataType* a;int top;int capacity;
}ST;//初始化
void STInit(ST* ps);
//销毁
void STDestroy(ST* ps);
//插入
void STPush(ST* ps, STDataType x);
//删除
void STPop(ST* ps);
//返回栈顶
STDataType STInsert(ST* ps);
//数量
int STSize(ST* ps);
//判断是否为空
int STEmpty(ST* ps);

Stack.c

#define _CRT_SECURE_NO_WARNINGS 1
#include"Stack.h"//初始化
void STInit(ST* ps)
{assert(ps);ps->a = NULL;ps->top = ps->capacity = 0;
}
//销毁
void STDestroy(ST* ps)
{assert(ps);free(ps->a);ps->a = NULL;ps->top = ps->capacity = 0;
}
//插入
void STPush(ST* ps, STDataType x)
{assert(ps);if (ps->top == ps->capacity){ps->capacity = ps->top == 0 ? 4 : ps->capacity*2;ps->a = (STDataType*)realloc(ps->a,sizeof(STDataType)*ps->capacity);}ps->a[ps->top] = x;ps->top++;
}
//删除
void STPop(ST* ps)
{assert(ps);assert(ps->top > 0);ps->top--;
}
//返回栈顶
STDataType STInsert(ST* ps)
{assert(ps);assert(ps->top > 0);return ps->a[ps->top-1];
}
//数量
int STSize(ST* ps)
{assert(ps);return ps->top;
}
//判断是否为空
int STEmpty(ST* ps)
{assert(ps);if (ps->top == 0){return 1;}else{return 0;}
}

然后我们就可以实现代码了；

我们的思路是：

将两边的下标存进【栈】，然后再取栈顶元素进行排序（霍尔或者其他），每取一个栈顶元素之后要把栈顶元素删除，然后再存放 keyi 两边的区间，再重复上面的过程，直至【栈】为空排序结束；

//快速排序(非递归)
void QuickNon(int* arr, int begin, int end)
{srand(time(0));ST ps;//初始化STInit(&ps);if (begin >= end){return;}//插入STPush(&ps, end);STPush(&ps, begin);//栈不为空就进去while (!STEmpty(&ps)){int left = STInsert(&ps);//栈顶元素STPop(&ps);//删除int right = STInsert(&ps);STPop(&ps);int keyi = PartSort1(arr, left, right);//排序[left,keyi-1] & [keyi+1,right]if (keyi + 1 < right){//插入STPush(&ps, right);STPush(&ps, keyi + 1);}if (left < keyi - 1){//插入STPush(&ps, keyi - 1);STPush(&ps, left);}}//销毁STDestroy(&ps);
}

我们运行测试一下：

可以看到也是完全 OK 的；

这就是快速排序的非递归实现！

三，快速排序源代码

以上的快速排序的全部代码如下（不包括【栈】）：

//三数取中
int middle(int* arr, int left, int right)
{//int mid = (left +right)/ 2;//随机数取中int mid = left + (rand() % (right - left));if (arr[left] < arr[mid]){if (arr[mid] < arr[right]){return mid;}if (arr[left] < arr[right]){return right;}else{return left;}}//arr[mid]<=arr[left]else{if (arr[mid] > arr[right]){return mid;}if (arr[left] > arr[right]){return right;}else{return left;}}
}//霍尔排序
int PartSort1(int* arr, int left, int right)
{//三数取中int ret = middle(arr, left, right);Swap(&arr[left], &arr[ret]);int keyi = left;while (left < right){//右边先走while (left<right && arr[right]>=arr[keyi]){right--;}//左边后走while (left < right && arr[left] <= arr[keyi]){left++;}//交换Swap(&arr[left], &arr[right]);}Swap(&arr[left], &arr[keyi]);return left;
}//挖坑法
int PartSort2(int* arr, int left, int right)
{//三数取中int ret = middle(arr, left, right);Swap(&arr[left], &arr[ret]);int key = arr[left];int hole = left;while (left < right){while (left < right && arr[right] >= key){right--;}arr[hole] = arr[right];hole = right;while (left < right && arr[left] <= key){left++;}arr[hole] = arr[left];hole = left;}arr[hole] = key;return hole;
}//前后指针法
int PartSort3(int* arr, int left, int right)
{//三数取中int ret = middle(arr, left, right);Swap(&arr[left], &arr[ret]);int keyi = left;int slow = left, fast = left+1;while (fast<=right){if (arr[fast] < arr[keyi] && ++slow!=fast){//交换Swap(&arr[fast], &arr[slow]);}fast++;}Swap(&arr[slow], &arr[keyi]);return slow;
}//插入排序(改造版)
void InsertSort1(int* arr, int left, int right)
{int i = 0;for (i = left; i < right; i++){int end = i;int tmp = arr[end + 1];while (end >= 0){if (arr[end] >= tmp){//交换Swap(&arr[end], &arr[end + 1]);end--;}else{break;}}arr[end + 1] = tmp;}
}//快速排序
void QuickSort(int* arr, int begin, int end)
{srand(time(0));if (begin >= end){return NULL;}if (end - begin <10){InsertSort1(arr,begin,end);}else{int keyi = PartSort1(arr, begin, end);//排序[begin,keyi) & [keyi+1,end]QuickSort(arr, begin, keyi);QuickSort(arr, keyi + 1, end);}
}//快速排序(非递归)
void QuickNon(int* arr, int begin, int end)
{srand(time(0));ST ps;//初始化STInit(&ps);if (begin >= end){return;}//插入STPush(&ps, end);STPush(&ps, begin);//栈不为空就进去while (!STEmpty(&ps)){int left = STInsert(&ps);//栈顶元素STPop(&ps);//删除int right = STInsert(&ps);STPop(&ps);int keyi = PartSort1(arr, left, right);//排序[left,keyi-1] & [keyi+1,right]if (keyi + 1 < right){//插入STPush(&ps, right);STPush(&ps, keyi + 1);}if (left < keyi - 1){//插入STPush(&ps, keyi - 1);STPush(&ps, left);}}//销毁STDestroy(&ps);
}
 特性总结：

1，快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序

2.，时间复杂度：O(N*logN)

3.，空间复杂度：O(logN) 

4， 稳定性：不稳定

第三阶段就到这里了，带大家啃块硬骨头磨磨牙！

后面博主会陆续更新；

如有不足之处欢迎来补充交流！

完结。。

再次祝大家国庆节快乐！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/98038.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Decorator

Decorator

Decorator 动机 在某些情况下我们可能会“过度地使用继承来扩展对象的功能”&#xff0c; 由于继承为类型引入的静态特质&#xff0c;使得这种扩展方式缺乏灵活性&#xff1b; 并且随着子类的增多&#xff08;扩展功能的增多&#xff09;&#xff0c;各种子类的组合&#xff…
阅读更多...
typescript: Builder Pattern

typescript: Builder Pattern

/*** file: CarBuilderts.ts* TypeScript 实体类 Model* Builder Pattern* 生成器是一种创建型设计模式&#xff0c; 使你能够分步骤创建复杂对象。* https://stackoverflow.com/questions/12827266/get-and-set-in-typescript* https://github.com/Microsoft/TypeScript/wiki/…
阅读更多...
用这些IDEA插件，让你早下班两小时

用这些IDEA插件，让你早下班两小时

GenerateAllSetter:一键调用一个对象的所有setter方法 RestfulTool:自动显示所有URL接口&#xff0c;快速检索接口 SequenceDiagram:以图形界面形式显示方法调用链&#xff0c;方便阅读源码、梳理代码 CamelCase:变量下划线转驼峰命名 Rainbow Brackets:帮助程序员识别代码中括…
阅读更多...
SpringCloud Alibaba - Sentinel 限流规则（案例 + JMeter 测试分析）

SpringCloud Alibaba - Sentinel 限流规则（案例 + JMeter 测试分析）

目录 一、Sentinel 限流规则 1.1、簇点链路 1.2、流控模式 1.2.1、直接流控模式 1.2.2、关联流控模式 a&#xff09;在 OrderController 中新建两个端点. b&#xff09;在 Sentinel 控制台中对订单查询端点进行流控 c&#xff09;使用 JMeter 进行测试 d&#xff09;分…
阅读更多...
Aurora中的策略模式和模板模式

Aurora中的策略模式和模板模式

Aurora中的策略模式和模板模式 在aurora中为了方便以后的扩展使用了策略模式和模板模式实现图片上传和搜索功能&#xff0c;能够在配置类中设置使用Oss或者minio上传图片&#xff0c;es或者mysql文章搜索。后续有新的上传方式或者搜索方式只需要编写对应的实现类即可&#xff…
阅读更多...
【C++设计模式之迭代器模式】分析及示例

【C++设计模式之迭代器模式】分析及示例

简介 迭代器模式是一种行为型设计模式&#xff0c;它提供了一种顺序访问聚合对象元素的方法&#xff0c;而又不需要暴露聚合对象的内部结构。迭代器模式通过将遍历算法封装在迭代器对象中&#xff0c;可以使得遍历过程更简洁、灵活&#xff0c;并且符合开闭原则。 描述 迭代…
阅读更多...
延时队列java

延时队列java

Redis过期键通知&#xff08;使用redis来实现延迟通知&#xff09; Slf4j public class KeyExpiredListener extends KeyExpirationEventMessageListener {public KeyExpiredListener(RedisMessageListenerContainer listenerContainer) {super(listenerContainer);}Overridep…
阅读更多...
arm 点灯实验代码以及现象

arm 点灯实验代码以及现象

.text .global _start _start: 1.设置GPIOE寄存器的时钟使能 RCC_MP_AHB4ENSETR[4]->1 0x50000a28 LDR R0,0x50000A28 LDR R1,[R0] ORR R1,R1,#(0x1<<4) 第4位置1 STR R1,[R0] 1.设置GPIOF寄存器的时钟使能 RCC_MP_AHB4ENSETR[4]->1 0x50000a28 LDR R…
阅读更多...
Unity可视化Shader工具ASE介绍——3、ASE的Shader类型介绍

Unity可视化Shader工具ASE介绍——3、ASE的Shader类型介绍

大家好&#xff0c;我是阿赵。这里继续介绍Unity可视化Shader编辑插件ASE的用法。   上一篇介绍了节点的输入输出节点。这一篇来介绍一下不同的Shader类型的区别。 一、修改Shader类型 之前介绍创建Shader的时候&#xff0c;曾经说过可以选择Shader的类型。 其实这个类型是…
阅读更多...
FFmpeg 命令：从入门到精通 | ffmpeg 命令视频录制

FFmpeg 命令：从入门到精通 | ffmpeg 命令视频录制

FFmpeg 命令&#xff1a;从入门到精通 | ffmpeg 命令视频录制 FFmpeg 命令&#xff1a;从入门到精通 | ffmpeg 命令视频录制安装软件&#xff1a;Screen Capturer Recorder查看可用设备名字音视频录制录制视频&#xff08;默认参数&#xff09;录制声音&#xff08;默认参数&am…
阅读更多...
ArcGIS Engine：视图菜单的创建和鹰眼图的实现

ArcGIS Engine：视图菜单的创建和鹰眼图的实现

目录 01 创建项目 1.1 通过ArcGIS-ExtendingArcObjects创建窗体应用 1.2 通过C#-Windows窗体应用创建窗体应用 1.2.1 创建基础项目 1.2.2 搭建界面 02 创建视图菜单 03 鹰眼图的实现 3.1 OnMapReplaced事件的触发 3.2 OnExtentUpdated事件的触发 04 稍作演示 01 创建项目…
阅读更多...
Qt单一应用实例判断

Qt单一应用实例判断

原本项目中使用QSharedMemory的方法来判断当前是否已存在运行的实例&#xff0c;但在MacOS上&#xff0c;当程序异常崩溃后&#xff0c;QSharedMemory没有被正常销毁&#xff0c;导致应用程序无法再次被打开。 对此&#xff0c;Qt assistant中有相关说明&#xff1a; 摘抄 qt-s…
阅读更多...
Spring源码解析——IOC属性填充

Spring源码解析——IOC属性填充

正文 doCreateBean() 主要用于完成 bean 的创建和初始化工作&#xff0c;我们可以将其分为四个过程&#xff1a; 最全面的Java面试网站 createBeanInstance() 实例化 beanpopulateBean() 属性填充循环依赖的处理initializeBean() 初始化 bean 第一个过程实例化 bean在前面一篇…
阅读更多...
卷积层与池化层输出的尺寸的计算公式详解

卷积层与池化层输出的尺寸的计算公式详解

用文字简单表述如下 卷积后尺寸计算公式&#xff1a; (图像尺寸-卷积核尺寸 2*填充值)/步长1 池化后尺寸计算公式&#xff1a; (图像尺寸-池化窗尺寸 2*填充值)/步长1 一、卷积中的相关函数的参数定义如下&#xff1a; in_channels(int) – 输入信号的通道 out_channels(int)…
阅读更多...
Vue3 reactive和ref详解

Vue3 reactive和ref详解

reactive Vue3.0中的reactive reactive 是 Vue3 中提供的实现响应式数据的方法。在 Vue2 中响应式数据是通过 defineProperty 来实现的&#xff0c;在 Vue3 中响应式数据是通过 ES6 的 Proxy来实现的。reactive 参数必须是对象 (json / arr)如果给 reactive 传递了其它对象 默…
阅读更多...
合宙Air780e+luatos+腾讯云物联网平台完成设备通信与控制（属性上报+4G远程点灯）

合宙Air780e+luatos+腾讯云物联网平台完成设备通信与控制（属性上报+4G远程点灯）

1.腾讯云物联网平台 首先需要在腾讯云物联网平台创建产品、创建设备、定义设备属性和行为&#xff0c;例如&#xff1a; &#xff08;1&#xff09;创建产品 &#xff08;2&#xff09;定义设备属性和行为 &#xff08;3&#xff09;创建设备 &#xff08;4&#xff09;准备参…
阅读更多...
【高阶数据结构】图详解第一篇：图的基本概念及其存储结构（邻接矩阵和邻接表）

【高阶数据结构】图详解第一篇：图的基本概念及其存储结构（邻接矩阵和邻接表）

文章目录 1. 图的基本概念1.1 什么是图1.2 有向图和无向图1.3 完全图1.4 邻接顶点1.5 顶点的度1.6 路径1.7 路径长度1.8 简单路径与回路1.9 子图1.10 连通图1.11 强连通图1.12 生成树 2. 图的存储结构2.1 邻接矩阵2.2 邻接矩阵代码实现结构定义构造函数添加边打印图测试 2.3 邻…
阅读更多...
ToBeWritten之改进威胁猎杀：自动化关键角色与成功沟通经验

ToBeWritten之改进威胁猎杀：自动化关键角色与成功沟通经验

也许每个人出生的时候都以为这世界都是为他一个人而存在的&#xff0c;当他发现自己错的时候&#xff0c;他便开始长大 少走了弯路&#xff0c;也就错过了风景&#xff0c;无论如何&#xff0c;感谢经历 转移发布平台通知&#xff1a;将不再在CSDN博客发布新文章&#xff0c;敬…
阅读更多...
10款录屏软分析与选择使用，只看这篇文章就轻松搞定所有，高清4K无水印录屏，博主UP主轻松选择

10款录屏软分析与选择使用，只看这篇文章就轻松搞定所有，高清4K无水印录屏，博主UP主轻松选择

录屏软件整理 如下为录屏软件&#xff0c;通过思维导图展示分析介绍&#xff1a; https://www.drawon.cn/template/details/6522bd5e0dad9029a0b528e1 如下为整理的录屏软件列表 名称产地价格支持的平台下载地址说明OBS国外免费开源windows/linux/machttps://obsproject.co…
阅读更多...
linux 笔记:远程服务器登录jupyter notebook

linux 笔记:远程服务器登录jupyter notebook

1 生成jupyter notebook 配置文件&#xff08;服务器端&#xff09; jupyter notebook --generate-config #Writing default config to: /home/shuailiu/.jupyter/jupyter_notebook_config.py2 Ipython中设置密码&#xff08;服务器端&#xff09; 3 修改jupyter 配置文件&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023