一、题目大意

围棋棋盘，如果某个坐标上下左右的四个方向都存在棋子，那么ans+1，根据输入的棋子数量，求出ans的数量。

二、解题思路

题目中有说到如果程序不会结束，那么输出-1，这其实是无源之水，根本不会发生。

我们可以一列一列的循环，然后针对列建立一个树状数组（线段树也行，树状数组更快）

坐标比较大，需要离散化（离散化就是把有效坐标排好序去重放在数组里，然后用原坐标对应数字再数组元素的顺序来替换掉原坐标的算法，可以参阅《挑战程序设计》第三章-常用技巧精选，或者可以参考鄙人AOJ0531的拙作题解）本题目每个输入的棋子x和y是有效坐标，其余坐标均无效，因为没有棋子的行或列一定无法让ans+1。

之后根据列来排序，列一样的，就根据行来排序（pair默认的就行，first列，second行）

然后记录下每一行的最后一个棋子的坐标（可以定一个数组，初值设置1或0，循环一次所有的棋子，更新到每一行的最大列即可）

然后，同时记录一个bool型的标记数组，来代表某一行是否前面已经有个棋子，如下图

循环每一列的时候，把当前元素和当前列上一个元素之间的元素集体+1（树状数组操作）update（上一个元素的列+1，当前元素列-1，1）这里需要判断下上一个的列+1和当前列-1的大小，如果大于等于那就不要更新了

同时遇到每一行第一个棋子时，要把这一行标记上，然后这一行的位置更新到0（更新到0是因为这一行之前左边没有棋子，如果左边没有棋子，那么这些+1的情况，即便上下有子也不应该记录到答案里，为的就是防止下图中红色箭头的位置被错误记录了），这样下次再碰到这一行的棋子，就可以代表两者之间的部分位置可以加到答案里。

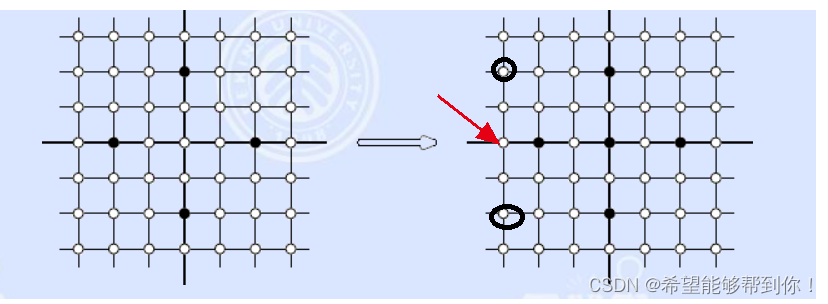
然后更新到每一行最后一列的时候（这里可以通过之前记录的行最大列的数组来判断是不是最后一列），如果这一行之前没有被标记过，即这一行的最后一个棋子左边没有棋子，那么这一行+1的那些坐标不算数，上下有子，右边也有，但是左边没有那就不行，直接continue。

如果这一行标记过，那那表左边有棋子，同时循环到的这一行的最后一个棋子是它右边的，然后更新树状数组时的区间边界是它上下的，那么树状数组求出这一行的数量，要加到ans里，我这个思路就是如下图所示，每一列右边的一些数子，就是遇到走过某一列的时候树状数组渲染到正常的样子（非树形求和的那种），然后红色的箭头的就代表走到某一行最后一列了增加ans，

表达的不清晰，见谅！

三、代码

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll;
typedef pair<int, int> P;
P num[100010];
ll bit0[131080], bit1[131080], ans;
int x[100010], y[100010], xLen, yLen, n, n_, maxCol[100010];
bool activeRow[100010];
void input()
{for (int i = 1; i <= n_; i++){scanf("%d%d", &num[i].first, &num[i].second);x[i] = num[i].first;y[i] = num[i].second;activeRow[i] = false;maxCol[i] = 1;}sort(x + 1, x + (1 + n_));sort(y + 1, y + (1 + n_));
}
void compress()
{xLen = 1;yLen = 1;for (int i = 2; i <= n_; i++){if (x[xLen] != x[i]){x[++xLen] = x[i];}if (y[yLen] != y[i]){y[++yLen] = y[i];}}for (int i = 1; i <= n_; i++){num[i].first = lower_bound(x + 1, x + (xLen + 1), num[i].first) - x;num[i].second = lower_bound(y + 1, y + (yLen + 1), num[i].second) - y;if (maxCol[num[i].second] < num[i].first){maxCol[num[i].second] = num[i].first;}}
}
void init()
{n = 131072;for (int i = 0; i <= n; i++){bit0[i] = 0LL;bit1[i] = 0LL;}
}
void updateBit0(int r, ll v)
{if (r <= 0){return;}for (int i = r; i <= n; i = i + (i & (-i))){bit0[i] = bit0[i] + v;}
}
void updateBit1(int r, ll v)
{if (r <= 0){return;}for (int i = r; i <= n; i = i + (i & (-i))){bit1[i] = bit1[i] + v;}
}
ll queryBit0(int r)
{ll sum = 0LL;for (int i = r; i > 0; i = i - (i & (-i))){sum = sum + bit0[i];}return sum;
}
ll queryBit1(int r)
{ll sum = 0LL;for (int i = r; i > 0; i = i - (i & (-i))){sum = sum + bit1[i];}return sum;
}
void update(int l, int r, ll v)
{updateBit0(l, (-1LL) * v * ((ll)(l - 1)));updateBit0(r + 1, v * ((ll)r));updateBit1(l, v);updateBit1(r + 1, (-1LL) * v);
}
ll query(int l, int r)
{ll allAmt = queryBit0(r);ll allAdd = queryBit1(r) * ((ll)r);ll leftAmt = queryBit0(l - 1);ll leftAdd = queryBit1(l - 1) * ((ll)(l - 1));return (allAmt + allAdd - leftAmt - leftAdd);
}
void solve()
{sort(num + 1, num + (1 + n_));ans = 0LL;for (int i = 1; i <= n_; i++){if (i > 1 && num[i - 1].first == num[i].first && (num[i - 1].second + 1) < num[i].second){update(num[i - 1].second + 1, num[i].second - 1, 1LL);}if (maxCol[num[i].second] == num[i].first && !activeRow[num[i].second]){continue;}if (maxCol[num[i].second] == num[i].first && activeRow[num[i].second]){ans = ans + query(num[i].second, num[i].second);}if (!activeRow[num[i].second]){ll oldVal = query(num[i].second, num[i].second);update(num[i].second, num[i].second, (-1LL) * oldVal);activeRow[num[i].second] = true;}}
}
int main()
{while (~scanf("%d", &n_)){input();compress();init();solve();ans = ans + ((ll)n_);printf("%lld\n", ans);}return 0;
}