引言：归并排序跟快速排序一样，都运用到了分治的算法，但是归并排序是一种稳定的算法，同时也具备高效，其时间复杂度为O(N*logN)

算法图解： 

 

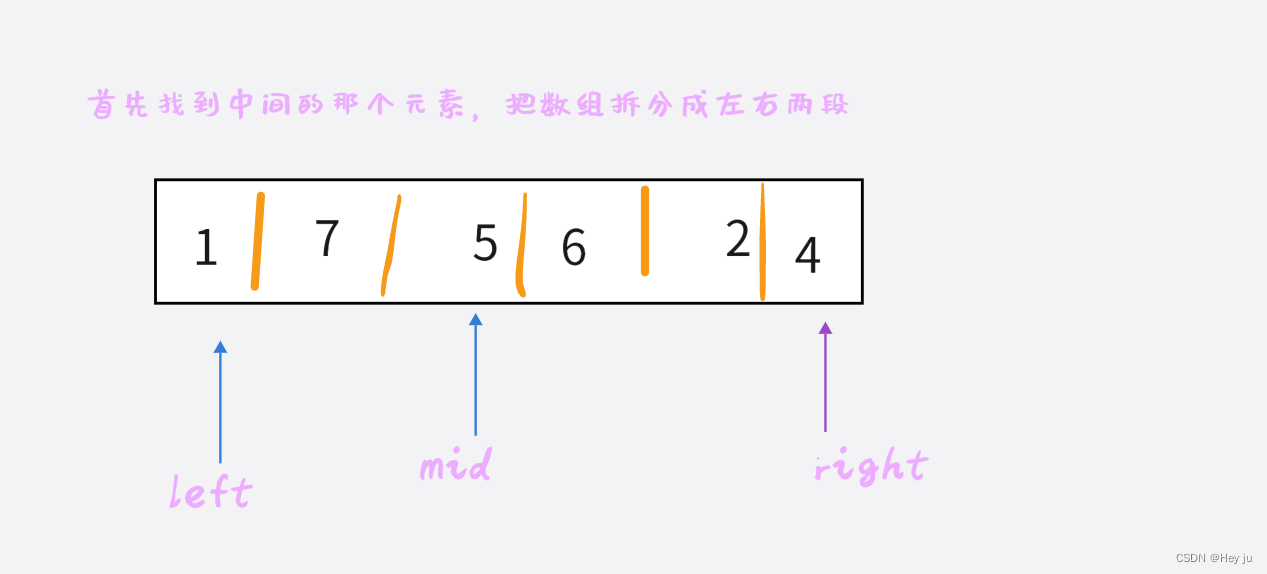
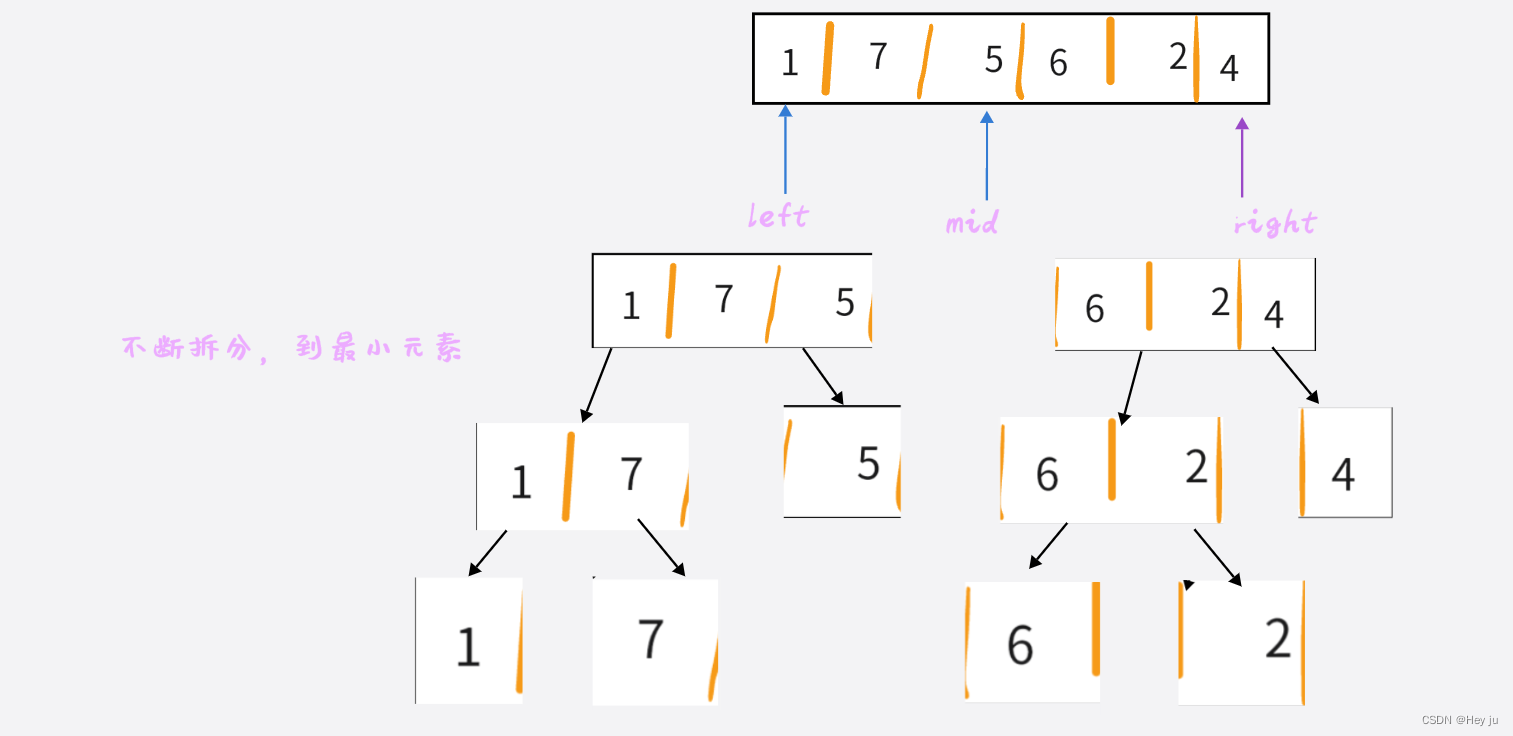
 然后开始归并：

 

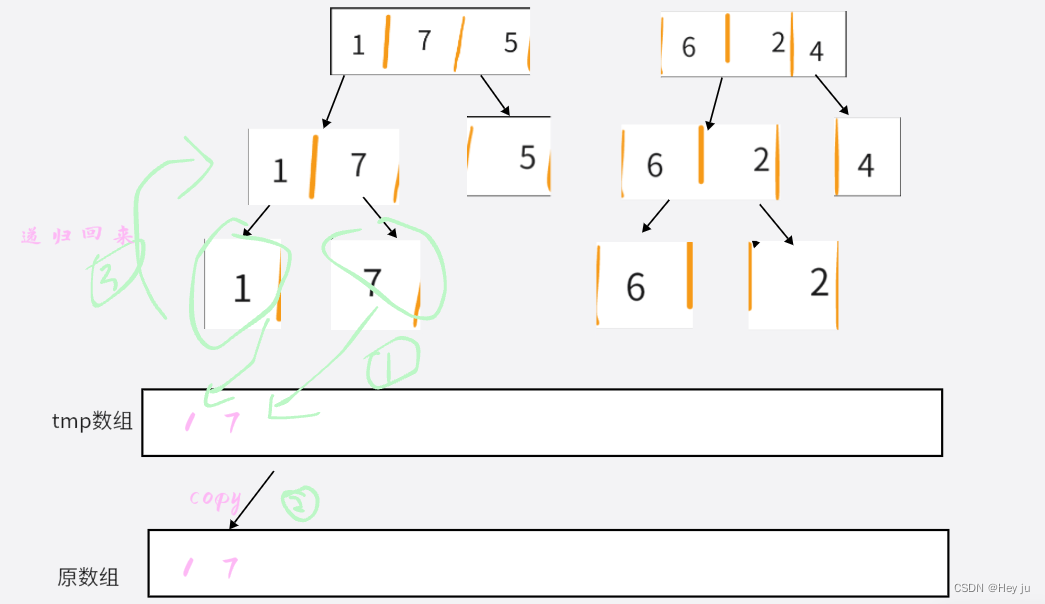
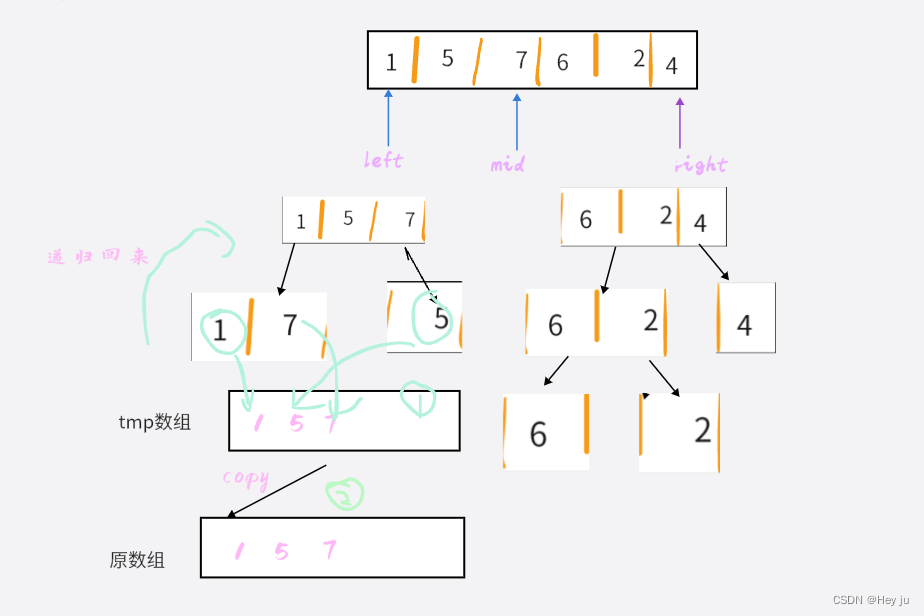 就是这个思想，拆成最小子问题后再进行归并（两个有序数组的排序问题）

下面是代码：

 

void merge_sort(int* arry, int size) {//保证接口一致性，再调子函数assert(arry);int* tmp = (int*)malloc(sizeof(int) * size);_merge(arry, 0, size - 1,tmp);//_merge2(arry, 0, size - 1, tmp);free(tmp);
}
void _merge(int* arry, int left, int right, int* tmp) {if (right - left <= 0)return;int mid = left + (right - left >> 1);//找到中间值//递归，拆分子问题_merge(arry, left, mid, tmp);_merge(arry, mid + 1, right, tmp);merge_arry(arry, left, mid, mid + 1, right, tmp);
}
void merge_arry(int* arry, int begin1, int end1, int begin2, int end2, int* tmp) {int index = begin1;int left = begin1;int right = end2;while (begin1 <= end1 && begin2 <= end2) {if (arry[begin1] < arry[begin2]) {tmp[index++] = arry[begin1++];}else {tmp[index++] = arry[begin2++];}}if (begin1 <= end1) {for (int i = begin1; i <= end1; i++) {tmp[index++] = arry[i];}}else {for (int i = begin2; i <= end2; i++) {tmp[index++] = arry[i];}}//再拷贝回原数组for (int i = left; i <= right; i++) {arry[i] = tmp[i];}
}

上面是它的递归实现，那么思考如何使用非递归实现呢？

 

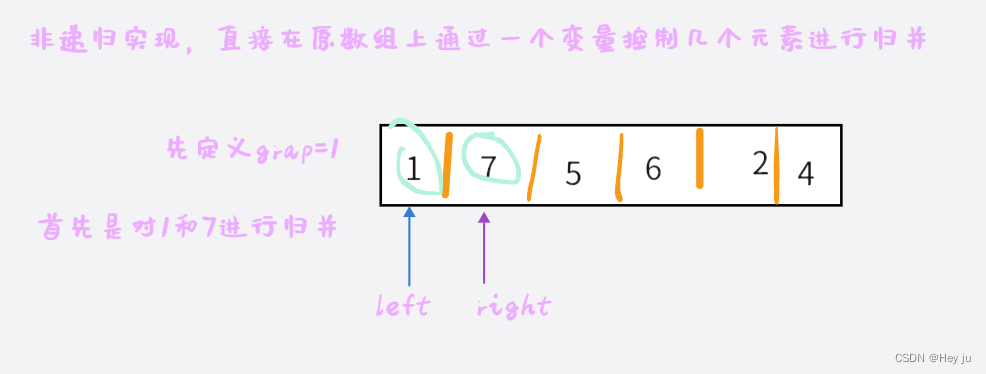
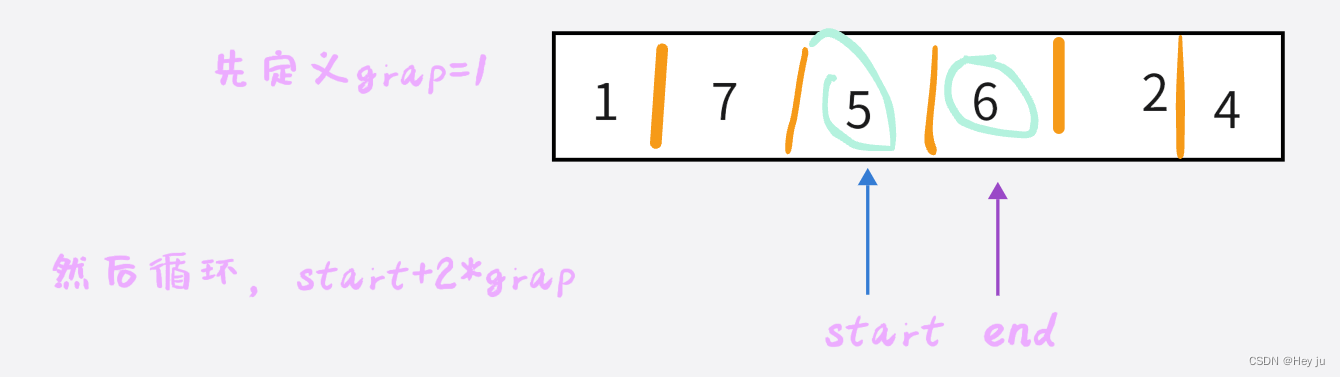
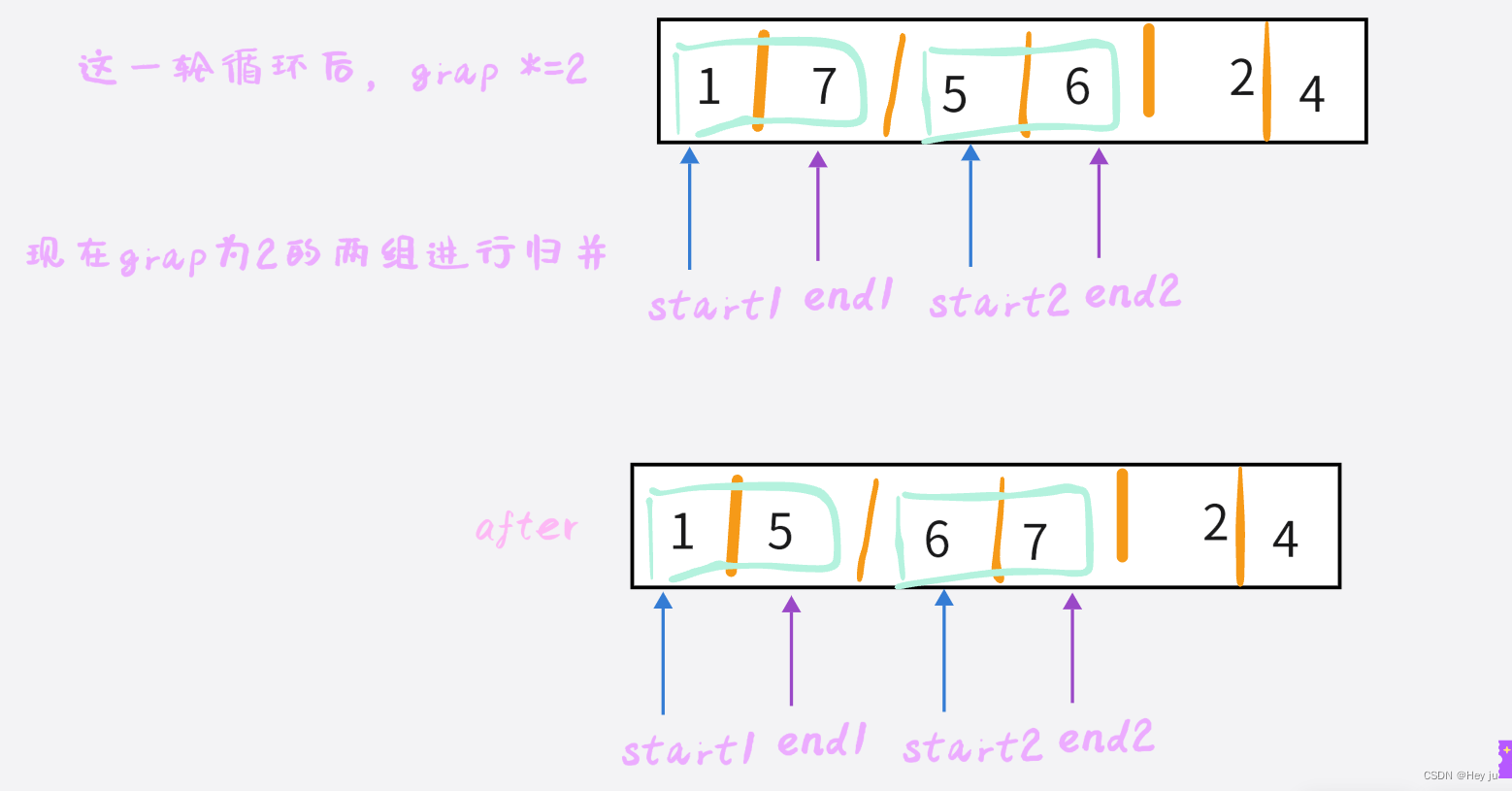 同时要控制grap的循环次数，grap小于等于数组大小即可

下面是代码：

void _merge2(int* arry, int left, int right, int* tmp) {int grap = 1;while (grap<=right+1) {for (int i = left; i <= right; i += 2 * grap) {int begin1 = i, end1 = i + grap - 1;int begin2 = i + grap, end2 = i + 2 * grap - 1;if (end1 > right)end1 = right;if (end2 > right)end2 = right;merge_arry(arry, begin1, end1, begin2, end2, tmp);}grap = grap * 2;}}
void merge_sort(int* arry, int size) {assert(arry);int* tmp = (int*)malloc(sizeof(int) * size);//_merge(arry, 0, size - 1,tmp);_merge2(arry, 0, size - 1, tmp);free(tmp);
}