CCF CSP认证 历年题目自练Day17
题目一
试题编号: 201803-1
试题名称: 跳一跳
时间限制: 1.0s
内存限制: 256.0MB
问题描述:
问题描述
近来,跳一跳这款小游戏风靡全国,受到不少玩家的喜爱。
简化后的跳一跳规则如下:玩家每次从当前方块跳到下一个方块,如果没有跳到下一个方块上则游戏结束。
如果跳到了方块上,但没有跳到方块的中心则获得1分;跳到方块中心时,若上一次的得分为1分或这是本局游戏的第一次跳跃则此次得分为2分,否则此次得分比上一次得分多两分(即连续跳到方块中心时,总得分将+2,+4,+6,+8…)。
现在给出一个人跳一跳的全过程,请你求出他本局游戏的得分(按照题目描述的规则)。
输入格式
输入包含多个数字,用空格分隔,每个数字都是1,2,0之一,1表示此次跳跃跳到了方块上但是没有跳到中心,2表示此次跳跃跳到了方块上并且跳到了方块中心,0表示此次跳跃没有跳到方块上(此时游戏结束)。
输出格式
输出一个整数,为本局游戏的得分(在本题的规则下)。
样例输入
1 1 2 2 2 1 1 2 2 0
样例输出
22
数据规模和约定
对于所有评测用例,输入的数字不超过30个,保证0正好出现一次且为最后一个数字。
题目分析(个人理解)
- 常规输入直接放到列表l=list(map(int,input().split()))
再看,输入1就加一分,2第一次出现就加两分,如果连续出现就累加2,即连续跳到方块中心时,总得分将+2,+4,+6,+8… - 那很好办,直接多分支语句就可以解决,我用a作为累加器,sum存放总得分。
- 直接上代码!!!
l=list(map(int,input().split()))
two=0
a=0
for i in range(len(l)):if l[i]==1:sum+=1a=0elif l[i]==2 and a==0:sum+=2a=2elif l[i]==2 and a!=0:a+=2sum+=aelif l[i]==0:break
print(sum)题目二
试题编号: 201803-2
试题名称: 碰撞的小球
时间限制: 1.0s
内存限制: 256.0MB
问题描述:
问题描述
数轴上有一条长度为L(L为偶数)的线段,左端点在原点,右端点在坐标L处。有n个不计体积的小球在线段上,开始时所有的小球都处在偶数坐标上,速度方向向右,速度大小为1单位长度每秒。
当小球到达线段的端点(左端点或右端点)的时候,会立即向相反的方向移动,速度大小仍然为原来大小。
当两个小球撞到一起的时候,两个小球会分别向与自己原来移动的方向相反的方向,以原来的速度大小继续移动。
现在,告诉你线段的长度L,小球数量n,以及n个小球的初始位置,请你计算t秒之后,各个小球的位置。
提示
因为所有小球的初始位置都为偶数,而且线段的长度为偶数,可以证明,不会有三个小球同时相撞,小球到达线段端点以及小球之间的碰撞时刻均为整数。
同时也可以证明两个小球发生碰撞的位置一定是整数(但不一定是偶数)。
输入格式
输入的第一行包含三个整数n, L, t,用空格分隔,分别表示小球的个数、线段长度和你需要计算t秒之后小球的位置。
第二行包含n个整数a1, a2, …, an,用空格分隔,表示初始时刻n个小球的位置。
输出格式
输出一行包含n个整数,用空格分隔,第i个整数代表初始时刻位于ai的小球,在t秒之后的位置。
样例输入
3 10 5
4 6 8
样例输出
7 9 9
样例说明
初始时,三个小球的位置分别为4, 6, 8。
 一秒后,三个小球的位置分别为5, 7, 9。
一秒后,三个小球的位置分别为5, 7, 9。

两秒后,第三个小球碰到墙壁,速度反向,三个小球位置分别为6, 8, 10。
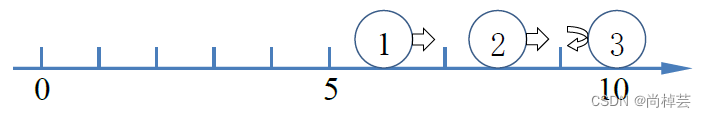
三秒后,第二个小球与第三个小球在位置9发生碰撞,速度反向(注意碰撞位置不一定为偶数),三个小球位置分别为7, 9, 9。

四秒后,第一个小球与第二个小球在位置8发生碰撞,速度反向,第三个小球碰到墙壁,速度反向,三个小球位置分别为8, 8, 10。

五秒后,三个小球的位置分别为7, 9, 9。

样例输入
10 22 30
14 12 16 6 10 2 8 20 18 4
样例输出
6 6 8 2 4 0 4 12 10 2
数据规模和约定
对于所有评测用例,1 ≤ n ≤ 100,1 ≤ t ≤ 100,2 ≤ L ≤ 1000,0 < ai < L。L为偶数。
保证所有小球的初始位置互不相同且均为偶数。
题目分析(个人理解)
- 题目又是又臭又长的感觉,不过意思很好理解,简而言之,将n个小球放到一个长为l的线段上,l是偶数,小球初始位置也是偶数,且开始方向都是向右,每个小球速度相同,碰到边缘或者碰到别的小球就换方向,由于长度和初始位置都是偶数所以不存在三个以及三个小球以上的小球碰撞的情况(题目有提示)。
- 还是先看输入,那就常规操作,都快打烂了。第一行输入n,L,t = list(map(int,input().split()))
- 第二行输入的是n个小球的初始位置positions=list(map(int,input().split()))
- 好!很好!关键的地方来了,注意输出,我们究竟要的是什么?是t时间后的每个小球的位置,我用一个空列表存储小球的运动方向,1表示向右运动,-1就是向左运动,位序就是小球的编号。
- 刚开始小球放上去都是向右运动的, 那直接用append()方法直接追加写入1。
6.== 对于碰撞的情况有三种,第一种,碰到右壁换方向,第二种,碰到左壁换方向,这两种情况很好解决,直接判断positions的值,如果是0意味着碰左壁,大于等于 l 意味着碰右壁,第三种是小球两两碰撞后改变方向,这种情况要注意发生的位置范围==。 - positions的值记录的是每个小球的当前位置,speed的值是动态的,根据碰撞情况确定方向(1或-1),我从第一秒一直遍历到第t秒,再加上初始位置就是小球的最后位置。(这也是输出需要的值)
然后遍历positions列表输出即可!! - 第三种情况怎么解决?positions的位序代表小球编号,值代表位置,注意第三种情况只可能在位置为1到 l-1 位置发生。只有两个小球碰撞的情况,所以直接遍历比较编号为k和k+1的小球的positons的值如果相等我就改变k和k+1小球的运动方向。
- 上代码!!!
n,L,t = list(map(int,input().split()))
positions=list(map(int,input().split()))
speed = []
for i in range(n):speed.append(1)
for j in range(t):for k in range(n):if positions[k] <= 0 or positions[k] >= L:speed[k] = -speed[k]for l in range(k+1,n):if positions[k] == positions[l]:speed[k] = -speed[k]speed[l] = -speed[l]for m in range(n):positions[m] += speed[m]
for o in range(n):print(positions[o],end=" ")总结
在这个最容易躁动的年纪想要沉下心来做忠于自己内心的事情确实是一件难事。——————shangzhaoyun 2023.9.30




![[Machine learning][Part3] numpy 矢量矩阵操作的基础知识](http://pic.xiahunao.cn/[Machine learning][Part3] numpy 矢量矩阵操作的基础知识)









——脉冲雷达(四))







