堆
是完全二叉树，类似这种样式的
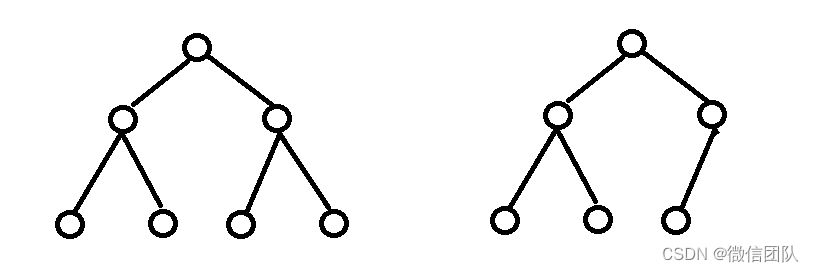
而这种有右子节点，没左子节点的就不是完全二叉树
分为大根堆和小根堆
大根堆是二叉树里每一颗子树的父节点都是这颗子树里最大的，即每一棵子树最大值是头节点的值
小根堆相反
把数组中从0开始的一段数人为想为完全二叉树
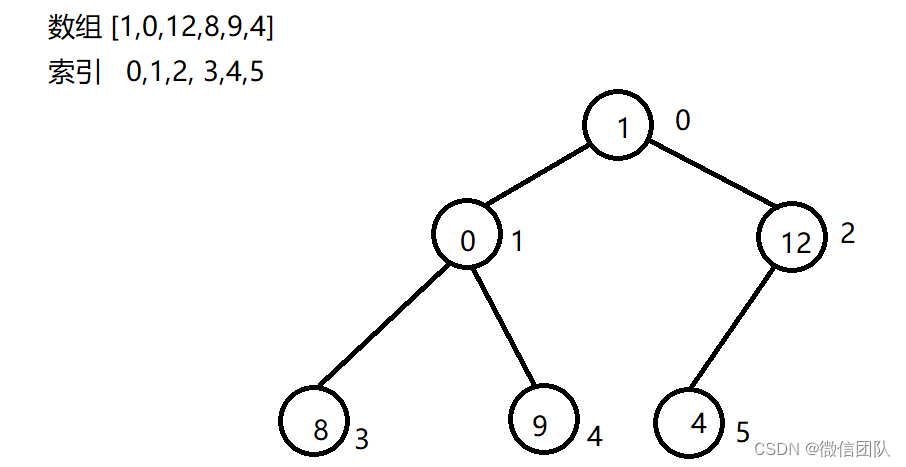
某一节点的数在数组中的索引是i，
则它的父节点为（i-1）/2，
它的左子节点为（2i+1），
右子节点为（2i+2）
堆结构的两种重要操作
向大根堆中添加一个数，heapinsert
如何把完全二叉树转化为大根堆（或者小根堆）
用一个变量记录当数组中从0开始的几个数是堆，heapsize，
1、开始时heapsize=0，即空堆，进来一个新数时，把新数放在堆的heapsize=0位置，此时heapsize=1
2、继续进新数放在heapsize=1位置，heapsize=2，然后新书和它的父节点进行比较，若小于等于父节点则不变，若大于父节点，则和父节点交换，交换之后继续和它的父节点比较，直到没父节点大或者到堆的顶了
3、进来新数继续重复上述操作
void heapInsert(int* arr, int index)
{while (arr[index] > arr[(index - 1) / 2]){swap2(arr[index], arr[(index - 1) / 2]);index = (index - 1) / 2;}
}
返回大根堆的最大值并移除，heapify
去掉大根堆的最大值，就是去掉最上面的数，用一个变量记录一下这个数，然后把大根堆最后一个数和该数进行交换，交换之后heapsize-1，然后头节点与左子节点和右子节点进行比较，三者中最大的左头节点，并交换，继续向下比直到该数大于左子节点和右子节点或者没有子节点
void heapIfy(int* arr, int index, int heapsize)//index是指从哪个位置往下做heapify
{int left = 2 * index + 1;while (left < heapsize)//该位置有左子节点{int largest;if ((left + 1 < heapsize) && (arr[left + 1] > arr[left]))//右子节点存在largest = left + 1;elselargest = left;if (arr[index] > arr[largest])largest = index;elselargest = largest;if (largest == index) break;swap2(arr[index], arr[largest]);//将父节点上和较大子节点的数交换index = largest;//交换后继续向下移进行比较left = 2 * index + 1;}
}
堆排序
先把数组变成大根堆，然后把最大数和最后位置上的数做交换，heapsize–，，此时最大值就到最后一位了，重复上述操作
void heapSort(int* arr, int L, int R)
{if (L >= R) return;//int heapsize = 0;for (int i = L; i < R + 1; i++){heapInsert(arr, i);//heapsize++;}int heapsize = R -L + 1;while (heapsize > 0){swap2(arr[L], arr[heapsize - 1]);heapsize = heapsize - 1;heapIfy(arr, L, heapsize);}
}
堆排序拓展题目
已知一个几乎有序的数组，几乎有序是指，如果把数组排好顺序的话，每个元素移动的距离可以不超过k，并且k相对于数组来说比较小。请选择一个合适的排序算法针对这个数据进行排序
比如k=6，先把数组中前7个数放到小根堆中，即0-6位置的数，在排完序之后，小根堆的最小值在0位置，因为k=6，所以7位置和7位置之后的数在排序时不会移动到0位置，所以排序后0位置上的数也是数组的最小值，把该数弹出
把7位置上的数加入到小根堆，此时最小值在1位置上，依次往后进行压数，弹数
使用系统自带的最小堆
void min_heapSortPlus(int* arr, int L, int R, int k)
{priority_queue<int, vector<int>, greater<int>> min_heap;int index = L;for (; index < L + k + 1; index++){min_heap.push(arr[index]);}int i = 0;for (; index < R + 1; i++, index++){arr[L + i] = min_heap.top();min_heap.push(arr[index]);min_heap.pop();}while (!min_heap.empty()){arr[L + i] = min_heap.top();min_heap.pop();i++;}
}
