1、打开Hyper-V安装
在地址栏输入控制面板,然后回车

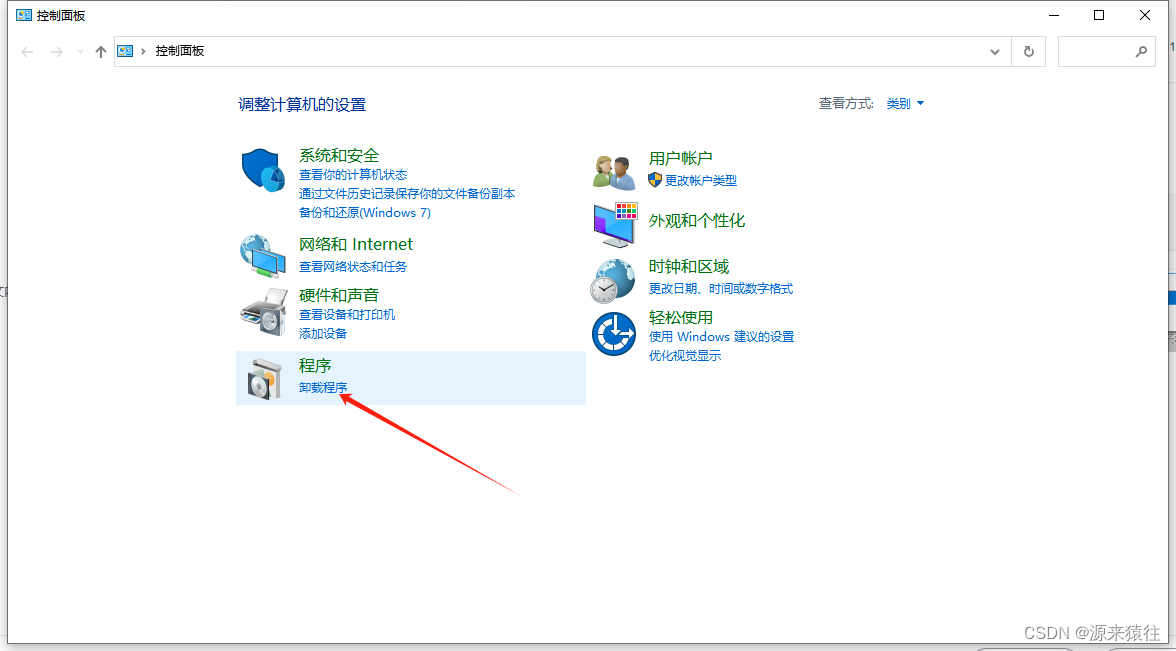
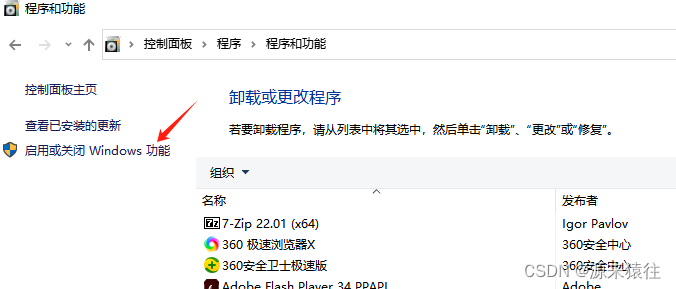
勾选Hyper-V安装,如果没有找到Hyper-V,那么请走第2步
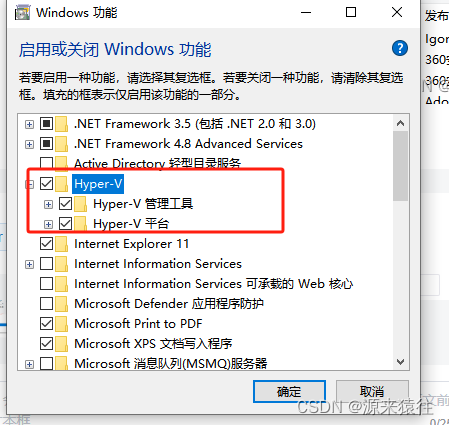
2、如果没有Hyper-V(可选)第一步无法打开
家庭版本需要开启Hyper-V
创建一个文本文档,后缀名称为.bat.名称随意,内容如下
pushd "%~dp0"
dir /b %SystemRoot%\servicing\Packages\*Hyper-V*.mum >hyper-v.txt
for /f %%i in ('findstr /i . hyper-v.txt 2^>nul') do dism /online /norestart /add-package:"%SystemRoot%\servicing\Packages\%%i"
del hyper-v.txt
Dism /online /enable-feature /featurename:Microsoft-Hyper-V-All /LimitAccess /ALL点击以管理员权限运行
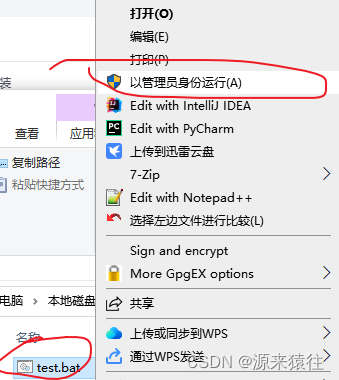
执行如下

添加注册表,在cmd 以管理员命令运行
REG ADD "HKEY_LOCAL_MACHINE\software\Microsoft\Windows NT\CurrentVersion" /v EditionId /T REG_EXPAND_SZ /d Professional /F3、下载docker
docker安装地址:https://docs.docker.com/desktop/install/windows-install/
如果上述地址打不开,那么提供csdn地址:
https://download.csdn.net/download/p731heminyang/89515514
4、安装docker
安装完成后,在cmd下面执行操作
5、执行
docker ps
![]()
正常如果出现此图那么意味着安装成功了。
【密钥生成介绍及算法规格】)





视频画面)

)









)
)