文章目录
- 一维数组
- 二维数组
- 特殊矩阵
- 对称矩阵
- 三角矩阵
- 三对角矩阵
- 稀疏矩阵
- 三元组法
- 十字链表法
一维数组
以一维数组A[0...n-1]为例,其存储结构关系式为
LOC ( a i ) = LOC ( a 0 ) + i × L ( 0 ⩽ i < n ) \operatorname{LOC}\left(a_i\right)=\operatorname{LOC}\left(a_0\right)+i \times L \quad(0 \leqslant i<n) LOC(ai)=LOC(a0)+i×L(0⩽i<n)
其中 L L L是每个数组元素所占的存储单元。
若以一维数组A[1...n]为例,其存储结构关系式为
LOC ( a i ) = LOC ( a 0 ) + ( i − 1 ) × L ( 1 ⩽ i ⩽ n ) \operatorname{LOC}\left(a_i\right)=\operatorname{LOC}\left(a_0\right)+(i-1) \times L \quad(1 \leqslant i\leqslant n) LOC(ai)=LOC(a0)+(i−1)×L(1⩽i⩽n)
其中 L L L是每个数组元素所占的存储单元。
二维数组
对于多维数组,有两种映射方法:按行优先和按列优先。以二维数组为例,设二维数组的行下标与列下标的范围分别为 [ 0 , h 1 ] [0,h_1] [0,h1]与 [ 0 , h 2 ] [0,h_2] [0,h2]。
- 按行优先的存储结构式为: LOC ( a i , j ) = LOC ( a 0 , 0 ) + [ i × ( h 2 + 1 ) + j ] × L \operatorname{LOC}\left(a_{i, j}\right)=\operatorname{LOC}\left(a_{0,0}\right)+\left[i \times\left(h_2+1\right)+j\right] \times L LOC(ai,j)=LOC(a0,0)+[i×(h2+1)+j]×L

- 按列优先的存储结构式为: LOC ( a i , j ) = LOC ( a 0 , 0 ) + [ j × ( h 1 + 1 ) + i ] × L \operatorname{LOC}\left(a_{i, j}\right)=\operatorname{LOC}\left(a_{0,0}\right)+\left[j \times\left(h_1+1\right)+i\right] \times L LOC(ai,j)=LOC(a0,0)+[j×(h1+1)+i]×L

特殊矩阵
对称矩阵
对一个 n n n阶矩阵 A A A中的任意一个元素 a i , j a_{i,j} ai,j都有 a i , j = a j , i ( 1 ≤ i , j ≤ n ) a_{i,j}=a_{j,i}(1\leq i,j \leq n) ai,j=aj,i(1≤i,j≤n),则称为对称矩阵。若仍采用二维数组存放,则会浪费几乎一半的空间,为此将 n n n阶对称矩阵 A A A存放在一维数组 B [ n ( n + 1 ) / 2 ] B[n(n+1)/2] B[n(n+1)/2]中。
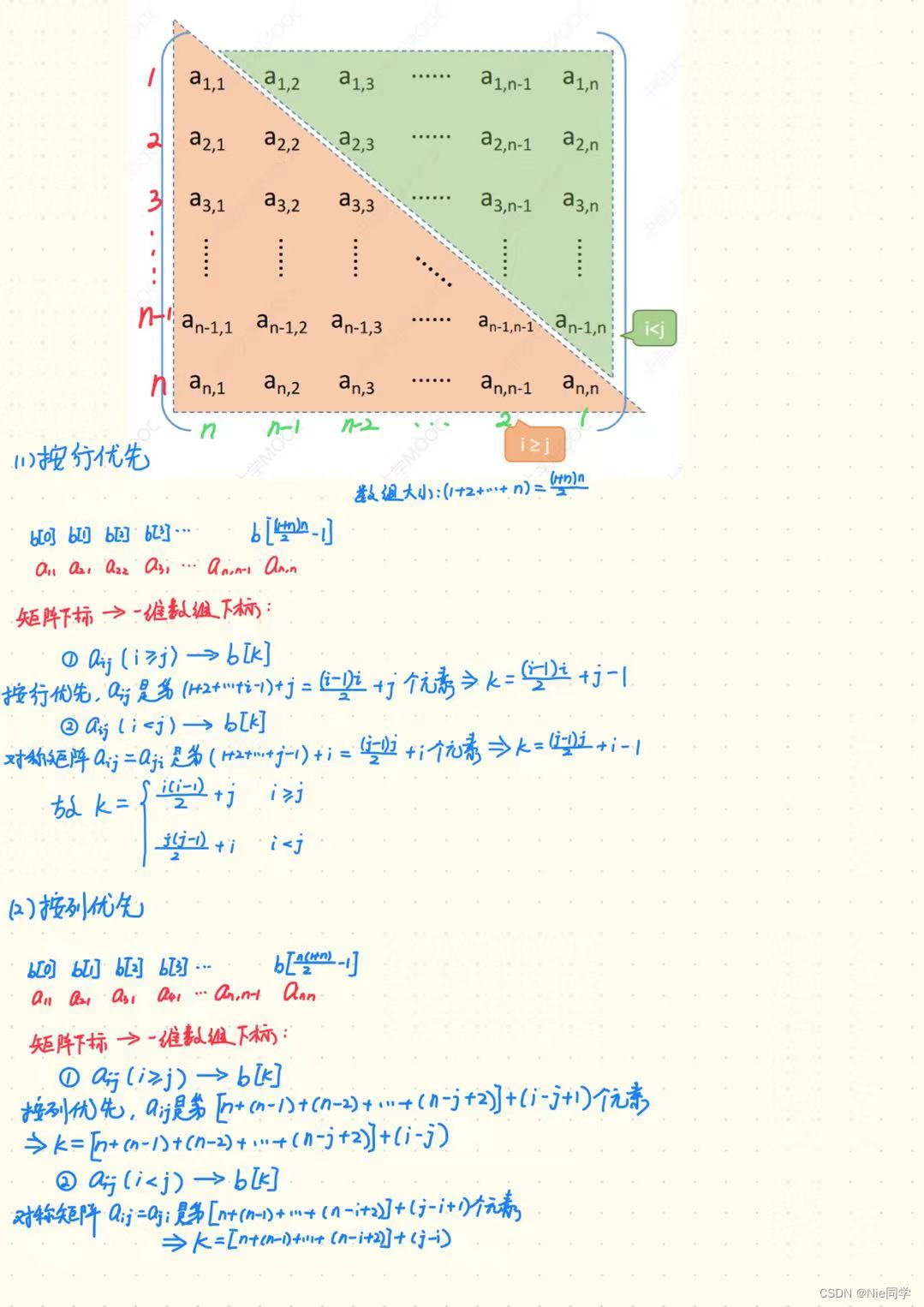
三角矩阵
下三角矩阵中,上三角区的所有元素均为同一常量。其存储思想与对称矩阵类似,不同之处在于存储完下三角区和主对角线上的元素之后,紧接着存储对角线上方的常量一次,所以可以将 n n n阶下三角矩阵 A A A压缩存储在 B [ n ( n + 1 ) / 2 + 1 ] B[n(n+1)/2+1] B[n(n+1)/2+1]中。

在数组 B B B中,位于元素 a i , j ( i ≥ j ) a_{i,j}(i\geq j) ai,j(i≥j)前面的元素个数为
第1行:1个元素
第2行:2个元素
……
第 i − 1 i-1 i−1行: i − 1 i-1 i−1个元素
第 i i i行: j j j个元素
故元素 a i , j a_{i,j} ai,j在数组 B B B中的下标(-1的目的是下标从0开始)
k = 1 + 2 + … … ( i − 1 ) + j − 1 = ( 1 + ( i − 1 ) ) ( i − 1 ) 2 + j − 1 = ( i − 1 ) i 2 + j − 1 k=1+2+……(i-1)+j-1=\frac{(1+(i-1))(i-1)}{2}+j-1=\frac{(i-1)i}{2}+j-1 k=1+2+……(i−1)+j−1=2(1+(i−1))(i−1)+j−1=2(i−1)i+j−1
元素下标之间的对应关系为
k = { i ( i − 1 ) 2 + j − 1 , i ⩾ j n ( n + 1 ) 2 , i < j k= \begin{cases}\frac{i(i-1)}{2}+j-1, & i \geqslant j \\ \frac{n(n+1)}{2}, & i<j \end{cases} k={2i(i−1)+j−1,2n(n+1),i⩾ji<j
上三角矩阵中,下三角区的所有元素均为同一常量。只需存储主对角线、上三角区上的元素和下三角区的常量一次,可将其压缩存储在 B [ n ( n + 1 ) / 2 + 1 ] B[n(n+1)/2+1] B[n(n+1)/2+1]中。
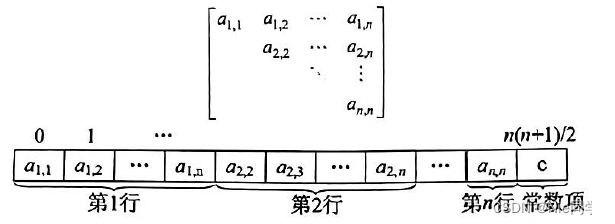
在数组 B B B中,位于元素 a i , j ( i ≤ j ) a_{i,j}(i≤j) ai,j(i≤j)前面的元素个数为
第1行: n n n个元素
第2行: n − 1 n-1 n−1个元素
……
第 i − 1 i-1 i−1行: n − i + 2 n-i+2 n−i+2个元素
第 i i i行: j − i + 1 j-i+1 j−i+1个元素( a i , i a_{i,i} ai,i开始到第 a i , j a_{i,j} ai,j该行一共有 j − i + 1 j-i+1 j−i+1个元素)
故元素 a i , j a_{i,j} ai,j在数组 B B B中的下标(-1的目的是下标从0开始)
k = n + ( n − 1 ) + … … + ( n − i + 2 ) + ( j − i + 1 ) − 1 = ( n + ( n − i + 2 ) ) ( i − 1 ) 2 + j − i = ( 2 n − i + 2 ) ( i − 1 ) 2 + j − i k=n+(n-1)+……+(n-i+2)+(j-i+1)-1=\frac{(n+(n-i+2))(i-1)}{2}+j-i=\frac{(2n-i+2)(i-1)}{2}+j-i k=n+(n−1)+……+(n−i+2)+(j−i+1)−1=2(n+(n−i+2))(i−1)+j−i=2(2n−i+2)(i−1)+j−i
元素下标之间的对应关系为
k = { ( 2 n − i + 2 ) ( i − 1 ) 2 + j − i , i ⩽ j n ( n + 1 ) 2 , i > j k= \begin{cases}\frac{(2n-i+2)(i-1)}{2}+j-i, & i \leqslant j \\ \frac{n(n+1)}{2}, & i>j \end{cases} k={2(2n−i+2)(i−1)+j−i,2n(n+1),i⩽ji>j
三对角矩阵
对角矩阵也称带状矩阵。对 n n n阶矩阵 A A A中的任意一个元素 a a a,当 ∣ i − j ∣ > 1 |i-j|>1 ∣i−j∣>1时,若有 a i , j = 0 ( 1 ≤ i , j ≤ n ) a_{i,j}=0 (1≤i,j≤n) ai,j=0(1≤i,j≤n),则称为三对角矩阵。
三对角矩阵 A A A也可以采用压缩存储,将3条对角线上的元素按行优先方式存放在一维数组 B B B中,且 a 1 , 1 a_{1,1} a1,1存放于 B [ 0 ] B[0] B[0]中,可将其压缩存储在 B [ 3 n − 2 ] B[3n-2] B[3n−2]中。
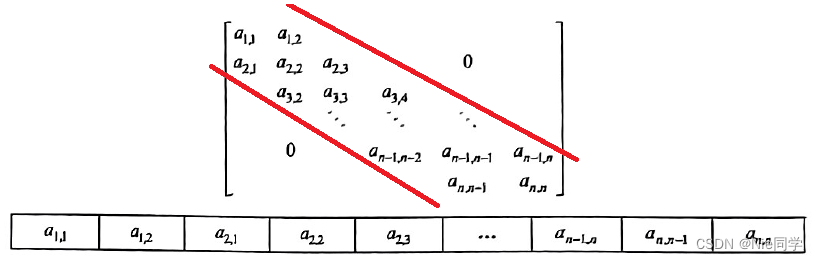
- a i , j → B [ k ] a_{i,j} \rightarrow B[k] ai,j→B[k]:即矩阵下标转换为压缩数组下标。
前 i − 1 i-1 i−1行: 3 ( i − 1 ) − 1 3(i-1)-1 3(i−1)−1个元素且 a i , j a_{i,j} ai,j是第 i i i行的第 j − i + 2 j-i+2 j−i+2个元素
故 a i , j a_{i,j} ai,j是第 3 ( i − 1 ) − 1 + ( j − i + 2 ) = 2 i + j − 2 3(i-1)-1+(j-i+2)=2i+j-2 3(i−1)−1+(j−i+2)=2i+j−2个元素,所以元素 a i , j ( 1 ≤ i , j ≤ n , ∣ i − j ∣ ≤ 1 ) a_{i,j}(1≤i,j≤n,|i-j|≤1) ai,j(1≤i,j≤n,∣i−j∣≤1)在一维数组 B B B中存放的下标为 k = 2 i + j − 3 k=2i+j-3 k=2i+j−3(下标从0开始,故要-1)。
- B [ k ] → a i , j B[k]\rightarrow a_{i,j} B[k]→ai,j:即压缩数组下标转换为矩阵下标。
根据三对角矩阵的定义: ∣ i − j ∣ ≤ 1 |i-j|\leq 1 ∣i−j∣≤1,可知 i − 1 ≤ j ≤ i + 1 i-1\leq j \leq i+1 i−1≤j≤i+1,根据 a i , j → B [ k ] a_{i,j} \rightarrow B[k] ai,j→B[k],可知 k = 2 i + j − 3 k=2i+j-3 k=2i+j−3,故有 i − 1 ≤ k + 3 − 2 i ≤ i + 1 i-1\leq k+3-2i\leq i+1 i−1≤k+3−2i≤i+1,有 3 ( i − 1 ) ≤ k + 1 ≤ 3 i − 1 3(i-1)\leq k+1 \leq 3i-1 3(i−1)≤k+1≤3i−1,有 i ≤ k + 1 3 + 1 i\leq\frac{k+1}{3}+1 i≤3k+1+1或 i ≥ k + 2 3 i\geq\frac{k+2}{3} i≥3k+2,故可以推出 i = ⌊ k + 1 3 + 1 ⌋ i=\lfloor\frac{k+1}{3}+1\rfloor i=⌊3k+1+1⌋或 i = ⌈ k + 2 3 ⌉ i=\lceil\frac{k+2}{3}\rceil i=⌈3k+2⌉,最后通过 j = k + 3 − 2 i j=k+3-2i j=k+3−2i,带入 i i i反算出 j j j来。
稀疏矩阵
矩阵中非零元素的个数 t t t,相对矩阵元素的个数 s s s来说非常少,即 s ≫ t s≫t s≫t的矩阵称为稀疏矩阵(结点数≫边数)。例如,一个矩阵的阶为 100 × 100 100×100 100×100,该矩阵中只有少于 100 100 100个非零元素。
三元组法
将非零元素及其相应的行和列构成一个三元组(行标 i i i,列标 j j j,值 a i , j a_{i,j} ai,j)。然后按照某种规律存储这些三元组线性表。稀疏矩阵压缩存储后便失去了随机存取特性。
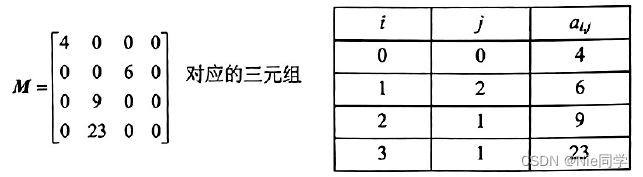
定义三元组结点
typedef struct {int data; // 数据域int i, j; // 行列坐标域
} Node;
定义三元组
typedef struct {Node s[Maxsize]; // 三元组数组int size; // 当前三元组元素个数
} Triplet;
十字链表法
为了解决三元组法中,压缩存储失去其随机存取特性,我们采用十字链表法,
十字链表法主要由以下几部分组成:
-
矩阵结点(Node): 每个节点包含以下字段:
- 行索引(rowIndex): 元素所在的行。
- 列索引(colIndex): 元素所在的列。
- 值(value): 元素的值。
- 行链表指针(right): 指向当前元素所在行的下一个非零元素。
- 列链表指针(down): 指向当前元素所在列的下一个非零元素。
-
行头节点(Row Header Nodes): 每一行的头节点,指向该行的第一个非零元素。
-
列头节点(Column Header Nodes): 每一列的头节点,指向该列的第一个非零元素。
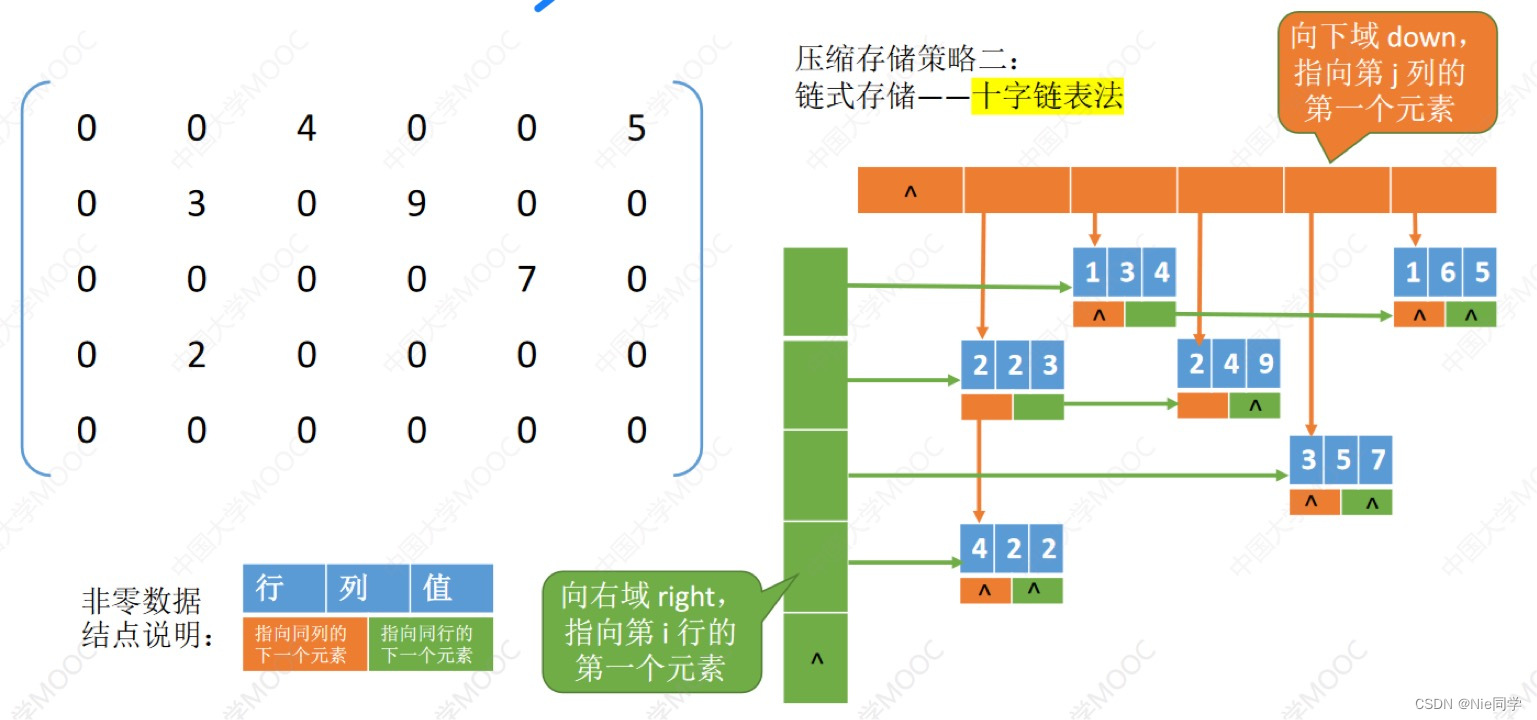
矩阵结点结构
typedef struct Node {int row, col;int value;struct Node *right, *down;
} Node;
十字链表结构
typedef struct {int rows, cols; // 行列坐标Node **row_heads; // 行头指针Node **col_heads; // 列头指针
} CrossLinkedList;




)
【原理扫描】)






)
![[面经] 西山居非正式面试(C++)](http://pic.xiahunao.cn/[面经] 西山居非正式面试(C++))





