🎉🎉🎉欢迎莅临我的博客空间，我是池央，一个对C++和数据结构怀有无限热忱的探索者。🙌

🌸🌸🌸这里是我分享C/C++编程、数据结构应用的乐园✨

🎈🎈🎈期待与你一同在编程的海洋中遨游，探索未知的技术奥秘💞

📝专栏指路:

📘【C++】专栏：深入解析C++的奥秘，分享编程技巧与实践。

📘【数据结构】专栏：探索数据结构的魅力，助你提升编程能力。

链表的回文结构

温馨小提示：点击即可做题，想回顾链表知识可以点击单链表和双链表。

必知知识：回文数

回文数是指一个整数，无论从左到右读还是从右到左读，其数字序列都是相同的。

题目：

画图分析：

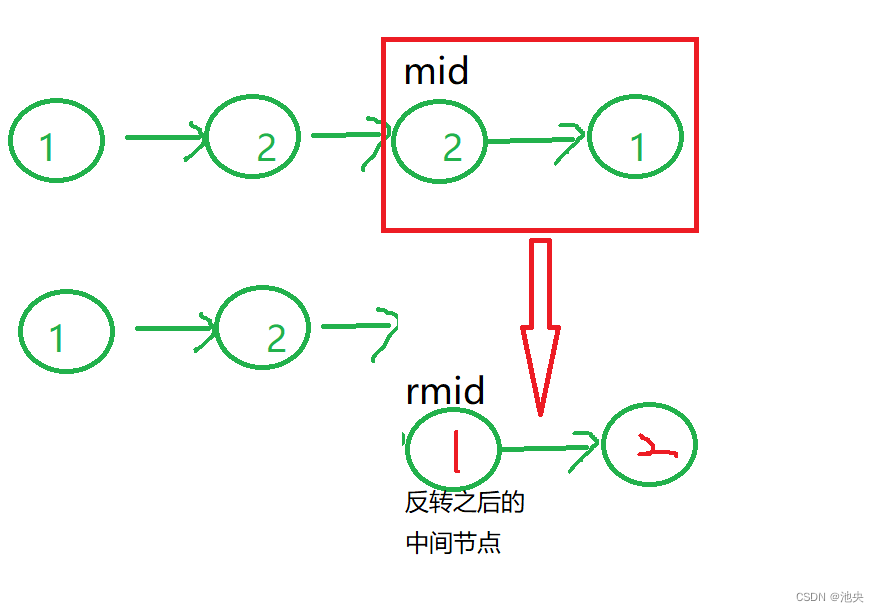
题目思路分析：

1.先找出中间节点

链表的中间节点（点击即可做题）找中间节点力扣上直接有这个题目，我们以此来分析思路

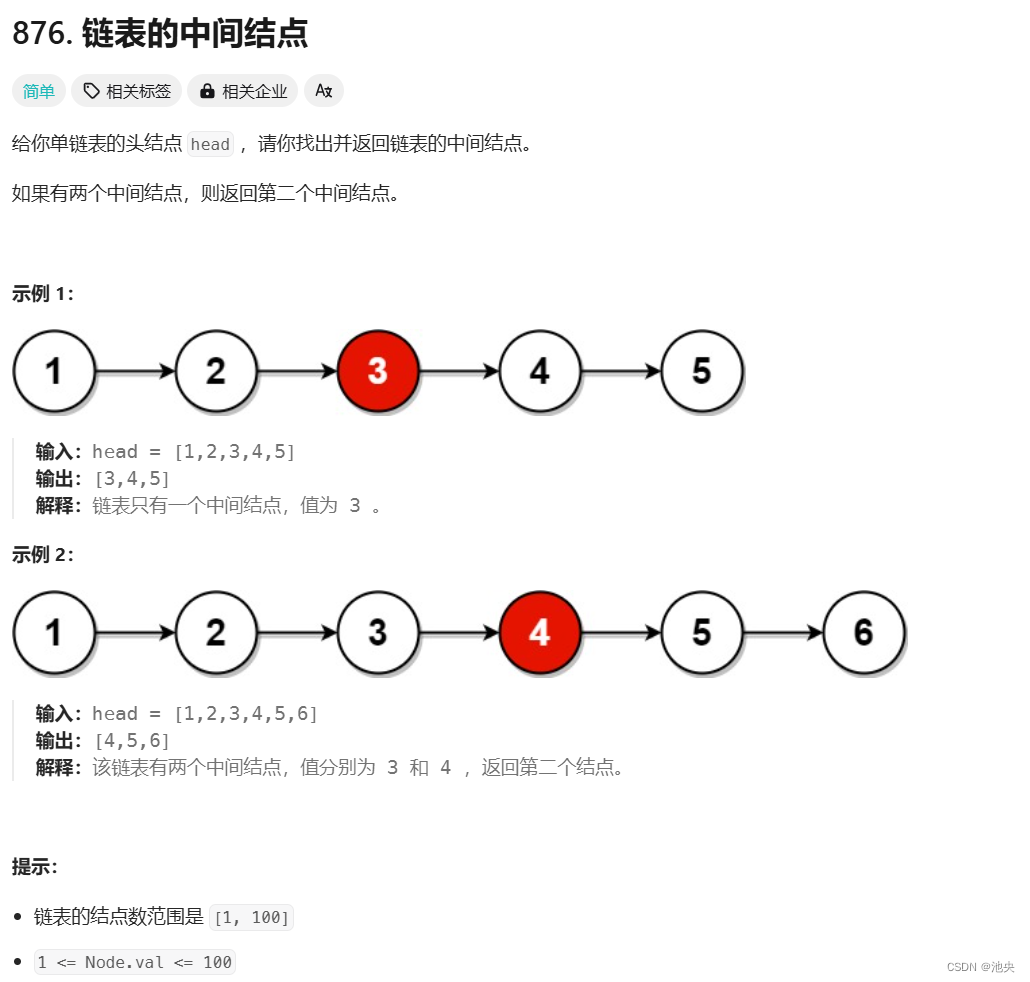
解决思路：快慢指针

快指针走两步，慢指针走一步

奇数个节点快指针的next指针为空时，慢指针刚好走到链表的中间节点

偶数个节点快指针为空时，慢指针刚好走到链表的中间节点

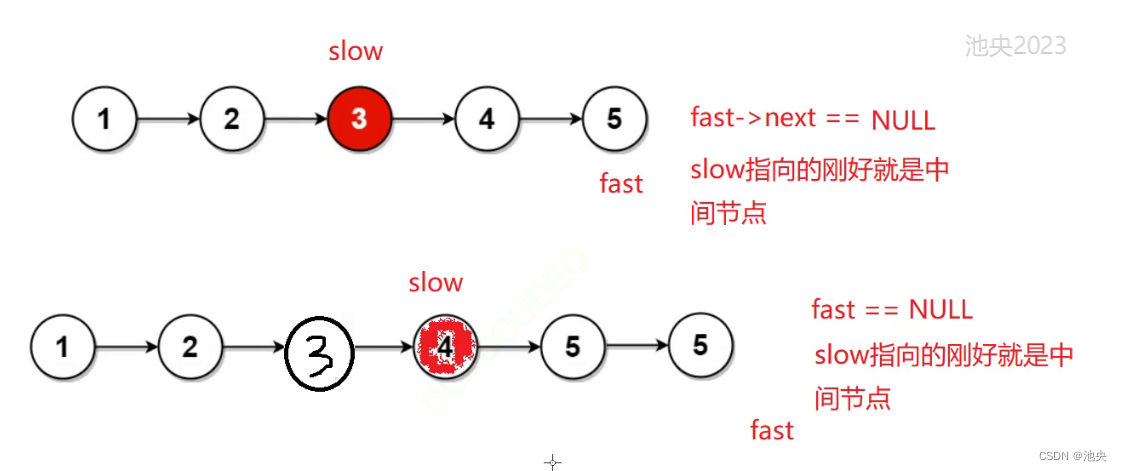
代码实现

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     struct ListNode *next;* };*/typedef struct ListNode ListNode;
struct ListNode* middleNode(struct ListNode* head) {//创建快慢指针，快指针走两步，慢指针走一步ListNode*fast,*slow;fast=head;slow=head;while(fast&&fast->next)//不可以换位置，在链表节点偶数个结束循环是fast==NULL,//交换位置会对空指针解引用{slow=slow->next;fast=fast->next->next;}return slow;
}

2.反转链表

反转链表（点击即可做题）找中间节点力扣上直接有这个题目，我们以此来分析思路

解决思路：迭代

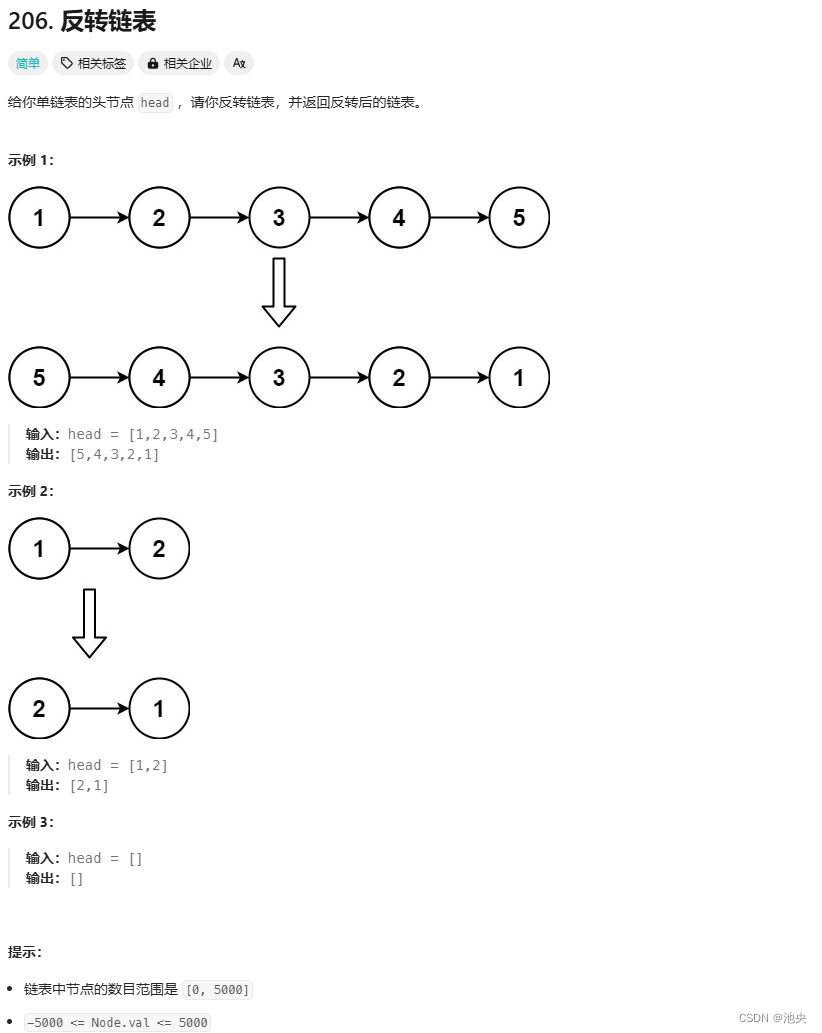
假设链表为 1→2→3→∅我们想要把它改成 ∅←1←2←3

我们需要定义三个指针

一个指针初始化为空

一个指针指向原链表的头结点

一个指针指向原链表头结点的next指针指向的节点

代码实现

struct ListNode*reverse(struct ListNode*head)
{if(head==nullptr||head->next==nullptr)//只有一个节点或链表为空{return head;}struct ListNode*n1,*n2,*n3;n1=nullptr;n2=head;n3=n2->next;//保存当前节点的next指针while(n2){n2->next=n1;//当前节点的next指针指向前一个节点n1=n2;n2=n3;if(n3)//n3最先为空此时n2还没有为空没有出循环，不能对空指针n3解引用n3=n3->next;}return n1;
};

最后我们来实现一下

链表回文结构的代码

// typedef struct ListNode ListNode;
// struct ListNode {
//     int val;
//     struct ListNode* next;
//     ListNode(int x) : val(x), next(NULL) {}
// };//寻找中间节点，快慢指针
struct ListNode*middleNode(struct ListNode*head)
{struct ListNode*fast,*slow;fast=head;slow=head;while(fast&&fast->next){slow=slow->next;fast=fast->next->next;}return slow;};
//翻转链表
struct ListNode*reverse(struct ListNode*head)
{if(head==nullptr||head->next==nullptr)//只有一个节点或链表为空{return head;}struct ListNode*n1,*n2,*n3;n1=nullptr;n2=head;n3=n2->next;while(n2){n2->next=n1;n1=n2;n2=n3;if(n3)//n3最先为空此时n2还没有为空没有出循环，不能对空指针n3解引用n3=n3->next;}return n1;
};class PalindromeList {public:bool chkPalindrome(ListNode* A) {struct ListNode*mid=middleNode(A);struct ListNode*rmid=reverse(mid);while(A&&rmid){if(A->val!=rmid->val){return false;}A=A->next;rmid=rmid->next;}return true;}
};

补充拓展

回文数是在数学中具有特殊的性质，也常被用于各种有趣的数学游戏和谜题中。

以下是关于回文数的几个关键点：

1.定义：设n是一个任意自然数，如果将其各位数字反向排列后得到的自然数n1与n相等，那么n就被称为回文数。例如，121、1331和12321都是回文数。
特征：
2.对称性：回文数的最大特点就是其对称性，无论从左到右还是从右到左读，数字序列都是相同的。
3.有限性：尽管正整数集是无限的，但回文数集却是有限的。对于任意给定的位数n，只有有限个n位回文数存在。例如，对于两位数，只有9个回文数（11、22、33、...、99）。
4.递增性：随着位数的增加，回文数的数量也呈现出递增的趋势。但这种递增并不是线性的，因为随着位数的增加，符合条件的回文数数量增长速度逐渐减慢。
5.生成方式：回文数可以通过多种方式生成。一种简单的方法是将一个数字反转后与原数字相加，重复这个过程直到得到一个回文数为止。例如，从数字4开始，我们得到4+4=8，8是回文数；从数字6开始，我们得到6+9=15，15不是回文数，但51+15=66，66是回文数。
6.数量统计：
1位数的回文数有9个（不包括0），它们的和是45。
2位数的回文数有9个，分别是11、22、33、...、99，它们的和是495。
3位数的回文数有90个，它们的和是49500。
7.应用：
在数学中，回文数是一种特殊的整数，研究回文数可以揭示整数的一些特殊性质和规律。例如，回文数和质数、完全平方数等数学概念相结合，可以产生一些有趣的数学问题和挑战。
在密码学和信息安全领域，回文数被用来构造强密码和加密算法，可以在一定程度上保证信息的加密和解密过程的安全性。
在诗歌、音乐等文化艺术中，回文数也具有一定的音韵美感和意象意义，可以用来构成一些优美的诗歌、歌词等。
 

持续更新中...

敬请期待