element-ui报表合计逻辑踩坑

1.快速实现一个合计

​ Element UI所提供的el-table中提供了方便快捷的合计逻辑实现：

​ https://element.eleme.cn/#/zh-CN/component/table

​ 此实现方法在官方文档中介绍详细，此处不多赘述。

​ 这里需要注意，el-table所提供的自定义求和方法summary-method所获得的返回值是一个一维数组。

​ 数组的顺序对应了列的顺序，以填充的方式将数组的值放入合计行。

2.实现一个多行合计的逻辑

​ 某些场景下，需要列表页同时展示总合计与本页合计，但是el-table实际提供的自定义方法仅支持一个一维数组，仅能支持一行合计行的快速实现。

​ 如果想要实现多行合计行，有以下两种方案：

​ 方案一：在自定义的合并方法中自定义包含HTML标签的返回值以实现复杂合计逻辑。

​ https://blog.csdn.net/qq_33475629/article/details/134008888

此博客实现了一行中的多个合计数据。

​ 详细可参考上述博客，此博客通过在vue代码中嵌入html标签实现了多行合并，核心代码如下：

getSummaries(param) {const { columns, data } = param;const sums = [];columns.forEach((column, index) => {if (index === 0) {// 通过<br/>实现换行，达到2行的效果sums[index] =  <p>当前页面总计<br/><br/>总计</p>;return;}let countArr = [];//element原本的总计：当前页面计算的值 集合const values = data.map((item) => Number(item[column.property]));if (!values.every((value) => isNaN(value))) {countArr[index] = values.reduce((prev, curr) => {const value = Number(curr);if (!isNaN(value)) {return prev + curr;} else {return prev;}}, 0);// 根据列表字段判断 取值if (column.property == 'total') {sums[index] = <p>{countArr[index]}<br/><br/>//第一行数据是当前页面值相加{this.apiData.account}<br/><br/>//第二行数据是后端接口返回</p>}} else {sums[index] = "-";}});return sums;},

效果图：

​ 实际逻辑为向summary-method所定义的自定义方法返回的数组中，直接放入HTML用于数据的填充。

​ 即如果数组中的值是value，则显示value；如果是HTML则会显示HTML。

​ 既然已经知道了合计行的自定义方法会如实返回HTML，那么对于一个原本只能返回一维数组的方法，我们可以向这个一维数组中塞入任何自定义的东西以实现复杂的逻辑——多行合计行分开。

​ https://blog.51cto.com/u_16213582/10217379

此博客实现了多行且不合并的逻辑。

​ 可进入此博客查阅，可发现其实现逻辑极其复杂，不乏在JS中额外关注字段名称、HTML布局的逻辑，所以不推荐此种写法。

​ 上述方案，单行实现尚可，但多行实现方案尽失优雅，故有以下方案二。

方案二：通过umy-ui中的u-table实现summary-method方法实现方便快捷的合计逻辑。

​ 官方文档：http://www.umyui.com/umycomponent/totalTable

u-table的合计与el-table的合计本质区别在于，u-table自定义方法返回值是一个二维数组。

​ u-table关于合计的实现与el-table大同小异：

​ 原el-table返回的一维数组只可返回一行，u-table通过返回一个二维数组，可实现返回多行，二维数组中每一个一位数组代表了一行合计行，且兼顾了自定义内容。其实现逻辑可参考官方文档，较之方案一方便快捷优雅。

​ 且umy-ui是由element-ui进行改造所得，且经过多次实践，可兼容element-ui，方案具有可行性。

​ 需要注意的是，当使用u-table时，因为u-table的结构与el-table不同而不可用，所以要针对u-table修改不分逻辑。

3.实现一个较为复杂的自定义多行合计逻辑

​ 基于2-方案二中所述，umy-ui同时提供了多行合计与自定义逻辑，关于自定义方法，官方文档的案例如下：

const values = data.map(item => Number(item[column.property]));
// 合计
if (!values.every(value => isNaN(value))) {means[columnIndex] = values.reduce((prev, curr) => {const value = Number(curr);if (!isNaN(value)) {return prev + curr;} else {return prev;}}, 0);// means[columnIndex] += ' 元'// 改变了ele的合计方式，扩展了合计场景// 你以为就只有上面这样玩吗？错啦，你还可以自定义样式哦// means[columnIndex] = '<span style="color: red">' + means[columnIndex] + '元</span>'means[columnIndex] = '<span style="color: red">' + means[columnIndex] + '元</span><br/><span>123</span>'
} else {means[columnIndex] = '';
}

​ 但是如果我们不满足于span或者br这种HTML原生标签，想要在每个单元格中使用el-button或者其他逻辑的组件。

​ 首先易于想到的办法为在summary-method中直接写入el-button，但是实际上组件在summary-method并不会成功被渲染，查阅后有博客说是因为当此方法执行时，表格已经渲染完毕，但el-button并不会第二次被渲染，从而无法成功插入自定义的组件。

​ 所以我们可知只需要当数据变动后，合计数据可以计算得出时，我们可以直接对DOM元素进行操作实现，再去手动插入el-button关联事件，那么我们可以对表格数据datas进行监听。

​ 实际案例如下：

// 自定义合计方法
getSummaries({ columns, data }) {let means = [] // 合计columns.forEach((column, columnIndex) => {if (columnIndex === columns.length - 7) {means.push('本页合计')return}const values = data.map((item) => Number(item[column.property]))// 合计if (!values.every((value) => isNaN(value))) {means[columnIndex] = values.reduce((prev, curr) => {const value = Number(curr)if (!isNaN(value)) {return prev + curr} else {return prev}}, 0)// 这里的值会有一个0.000000000001的精度损失，通过toFixed排除这种损失means[columnIndex] = formateNumber(means[columnIndex].toFixed(2))} else {means[columnIndex] = ''}})return [means, this.datasSummary]
}

  watch: {// 对datas进行监听datas: function() {let _this = thisthis.$nextTick(() => {// 获取合计那一行的DOMlet array = _this.$refs.mainTable.$refs.singleTable.$refs.footerWrapper.querySelector('.el-table__footer').querySelectorAll('td')let endNum = 0// 从倒数第六个开始遍历（因每行为6个，我只需要最后一行为按钮）for (let i = array.length - 6; endNum < 6; endNum++, i++) {let html = array[i].querySelector('.cell')let textContent = array[i].querySelector('.cell').textContent// 手动拼接按钮html.innerHTML = "<el-button type='text' style='cursor: pointer;color: #3b8bdb;' > " + textContent + '</el-button>'// 绑定click事件html.onclick = () => {switch (i) {case array.length - 6:_this.jumpToProvinceInventory(null, 'total', textContent)break}}}})}}

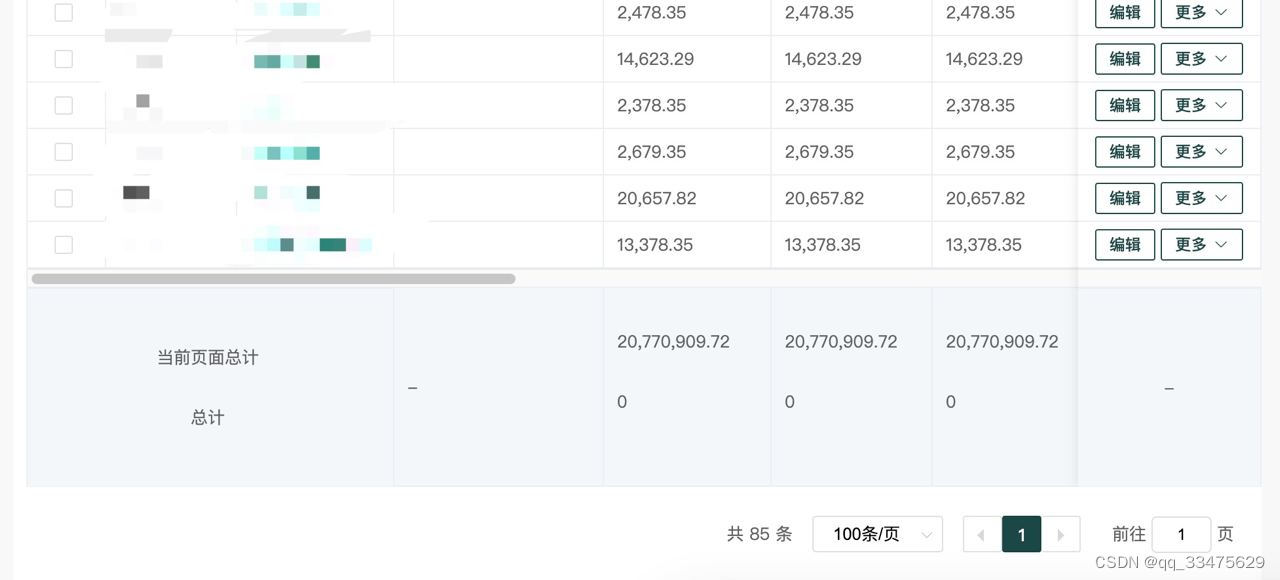
​ 最终的效果如下：

​ PS：此处的总合计数据为后台请求而来。

​ 使用合计时，偶尔会出现合计行加载不出或者加载慢的情况，其原因在于页面在渲染的时候，其实已经渲染出了合计行，但是合计行在计算布局的时候出现问题，导致合计行被列表页所遮挡（打开F12查看元素可发现），故没有展示。

​ 所以通过以下逻辑，手动重新计算布局即可解决：

<el-tableref="mainTable"show-summaryborder>
</el-table>

updated() {this.$nextTick(() => {this.$refs['mainTable'].doLayout()})
}