Leetcode刷题之合并两个有序数组
- 一、题目描述
- 二、题目解析
一、题目描述
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解释:需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
解释:需要合并 [1] 和 [] 。
合并结果是 [1] 。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1
输出:[1]
解释:需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。

二、题目解析
首先题目中,给了我们两个数组nums1和nums2。nums1和nums2是两个严格非递减的有序数组(也就是说除了递增,还有相等的情况)。我们需要将这两个数组合并成为一个新的数组,并将新的数组存放nums1数组当中。

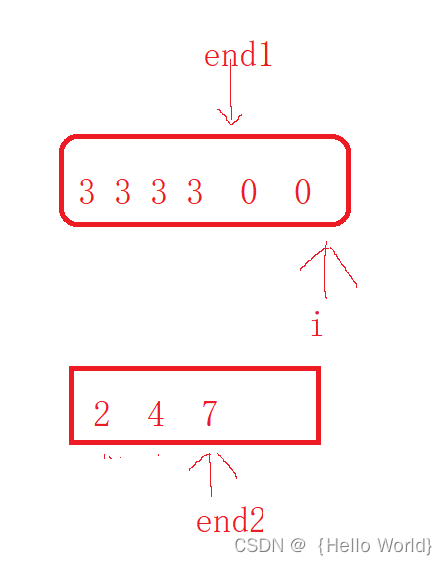
那么我们如何进行合并操作呢?我们可以首先在每一个数组的元素末端位置,分别定义两个变量,取名叫end1和end2。并且在nums1数组的最后一个位置再次定义一个i变量。
之后我们开始移动数据的位置。如果说,end2位置的数据大于end1数据位置的值时,我们将end2位置的值赋给数组nums1数组的i位置。并且让i和end2同时进行- -操作。反之则让end1位置的值赋给i,并且两个变量同时减减操作。当end2先减减到小于,这是第一种情况。因为nums1的元素被本身就存放在nums1数组中,并且元素本身就存在顺序,所以不用管。
第二种情况,就是end2数组中还有剩余元素,那么我们仅仅需要将其他元素继续放在i位置即可。如下图这种情况:
代码如下:
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){int end1=m-1;int end2=n-1;int i=m+n-1;while(end1>=0&&end2>=0){if(nums1[end1]<nums2[end2]){nums1[i]=nums2[end2];i--;end2--;}else{nums1[i]=nums1[end1];i--;end1--; }} while(end2>=0){nums1[i]=nums2[end2];i--;end2--;}
}