数据结构和算法(哈希表和图(A*算法精讲))

一、哈希表

1.1 哈希表原理精讲

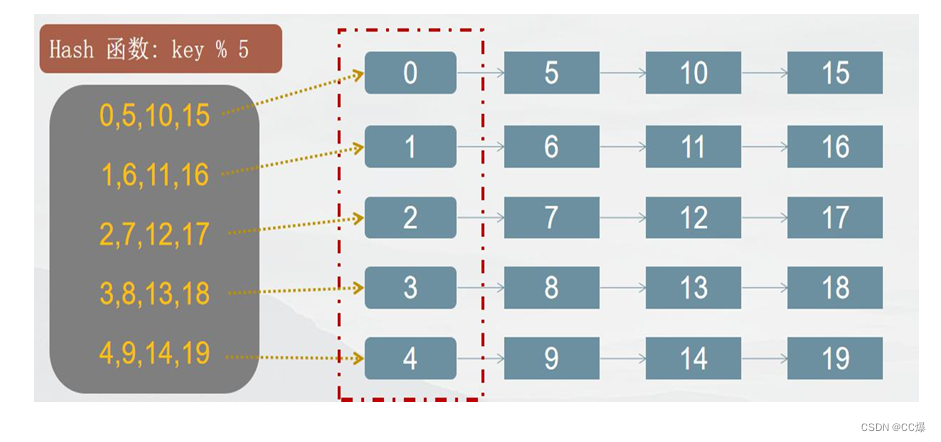
哈希表-散列表，它是基于快速存取的角度设计的，也是一种典型的“空间换时间”的做法

键(key)：组员的编号如，1、5、19。。。
值(value)：组员的其它信息（包含性别、年龄和战斗力等）
索引: 数组的下标(0,1,2,3,4)，用以快速定位和检索数据
哈希桶: 保存索引的数组(链表或数组)，数组成员为每一个索引值相同的多个元素
哈希函数: 将组员编号映射到索引上，采用求余法，如：组员编号 19
在这里插入图片描述

1.2 哈希链表算法实现

1.2.1 结构体定义

#define DEFAULT_SIZE 16/*哈希表元素定义*/
typedef struct _ListNode
{struct _ListNode* next;int key;void* data;
}ListNode;typedef ListNode*  List;
typedef ListNode*  Element;/*哈希表结构定义*/
typedef struct _HashTable
{int TableSize;List* Thelists;
}HashTable;

1.2.2 哈希函数

/*根据key计算索引，定位Hash桶的位置*/
int Hash(int key, int TableSize)
{return(key % TableSize);
}

1.2.3 链表初始化


/*初始化哈希表*/
HashTable* InitHash(int TableSize)
{int i = 0;HashTable* hTable = NULL;if (TableSize <= 0) {TableSize = DEFAULT_SIZE;}hTable = (HashTable*)malloc(sizeof(HashTable));if (NULL == hTable){printf("HashTable malloc error.\n");return NULL;}hTable->TableSize = TableSize;//为Hash桶分配内存空间，其为一个指针数组hTable->Thelists = (List*)malloc(sizeof(List) * TableSize);if (NULL == hTable->Thelists){printf("HashTable malloc error\n");free(hTable);return NULL;}//为Hash桶对应的指针数组初始化链表节点for (i = 0; i < TableSize; i++){hTable->Thelists[i] = (ListNode*)malloc(sizeof(ListNode));if (NULL == hTable->Thelists[i]){printf("HashTable malloc error\n");free(hTable->Thelists);free(hTable);return NULL;}else{memset(hTable->Thelists[i], 0, sizeof(ListNode));}}return hTable;
}

1.2.4 插入元素

/*从哈希表中根据键值查找元素*/
Element Find(HashTable* HashTable, int key)
{int i = 0;List L = NULL;Element e = NULL;i = Hash(key, HashTable->TableSize);L = HashTable->Thelists[i];e = L->next;while (e != NULL && e->key != key)e = e->next;return e;
}/*哈希表插入元素，元素为键值对*/
void Insert(HashTable* HashTable, int key, void* value)
{Element e = NULL, tmp = NULL;List L = NULL;e = Find(HashTable, key);if (NULL == e)  // 目前表中还不存在{tmp = (Element)malloc(sizeof(ListNode));if (NULL == tmp){printf("malloc error\n");return;}// 找到属于哪一个桶L = HashTable->Thelists[Hash(key, HashTable->TableSize)];tmp->data = value;tmp->key = key;tmp->next = L->next;L->next = tmp;   // 经典头插法}elseprintf("the key alreadye xist\n");
}

1.2.5 查找元素

/*从哈希表中根据键值查找元素*/
Element Find(HashTable* HashTable, int key)
{int i = 0;List L = NULL;Element e = NULL;i = Hash(key, HashTable->TableSize);L = HashTable->Thelists[i];e = L->next;while (e != NULL && e->key != key)e = e->next;return e;
}

1.2.6 删除元素

/*哈希表删除元素，元素为键值对*/
void Delete(HashTable* HashTable, int key)
{Element e = NULL, last = NULL;List L = NULL;int i = Hash(key, HashTable->TableSize);L = HashTable->Thelists[i];last = L;e = L->next;while (e != NULL && e->key != key) {last = e;e = e->next;}if (e) {//如果键值对存在last->next = e->next;delete(e);}
}

1.2.7 提取元素数据

/*哈希表元素中提取数据*/
void* Retrieve(Element e)
{return e ? e->data : NULL;
}

1.2.8 销毁

/*销毁哈希表*/
void Destory(HashTable* HashTable)
{int i = 0;List L = NULL;Element cur = NULL, next = NULL;for (i = 0; i < HashTable->TableSize; i++){L = HashTable->Thelists[i];cur = L->next;while (cur != NULL){next = cur->next;free(cur);cur = next;}free(L);}free(HashTable->Thelists);free(HashTable);
}

1.3 完整代码实现

bash.h 头文件

#pragma once
#define DEFAULT_SIZE 16/*哈希表元素定义*/
typedef struct _ListNode
{struct _ListNode* next;int key;void* data;
}ListNode;typedef ListNode*  List;
typedef ListNode*  Element;/*哈希表结构定义*/
typedef struct _HashTable
{int TableSize;List* Thelists;
}HashTable;/*哈希函数*/
int Hash(void* key, int TableSize);/*初始化哈希表*/
HashTable* InitHash(int ableSize);/*哈希表插入*/
void Insert(HashTable* HashTable, int key, void* value);/*哈希表查找*/
Element Find(HashTable* HashTable, int key);/*哈希表销毁*/
void Destory(HashTable*  HashTable);/*哈希表元素中提取数据*/
void* Retrieve(Element e);

bash.cpp 源文件

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include"hash.h"
#include<bits/stdc++.h>using namespace std;/*根据key计算索引，定位Hash桶的位置*/
int Hash(int key, int TableSize)
{return(key % TableSize);
}/*初始化哈希表*/
HashTable* InitHash(int TableSize)
{int i = 0;HashTable* hTable = NULL;if (TableSize <= 0) {TableSize = DEFAULT_SIZE;}hTable = (HashTable*)malloc(sizeof(HashTable));if (NULL == hTable){printf("HashTable malloc error.\n");return NULL;}hTable->TableSize = TableSize;//为Hash桶分配内存空间，其为一个指针数组hTable->Thelists = (List*)malloc(sizeof(List) * TableSize);if (NULL == hTable->Thelists){printf("HashTable malloc error\n");free(hTable);return NULL;}//为Hash桶对应的指针数组初始化链表节点for (i = 0; i < TableSize; i++){hTable->Thelists[i] = (ListNode*)malloc(sizeof(ListNode));if (NULL == hTable->Thelists[i]){printf("HashTable malloc error\n");free(hTable->Thelists);free(hTable);return NULL;}else{memset(hTable->Thelists[i], 0, sizeof(ListNode));}}return hTable;
}/*从哈希表中根据键值查找元素*/
Element Find(HashTable* HashTable, int key)
{int i = 0;List L = NULL;Element e = NULL;i = Hash(key, HashTable->TableSize);L = HashTable->Thelists[i];e = L->next;while (e != NULL && e->key != key)e = e->next;return e;
}/*哈希表插入元素，元素为键值对*/
void Insert(HashTable* HashTable, int key, void* value)
{Element e = NULL, tmp = NULL;List L = NULL;e = Find(HashTable, key);if (NULL == e){tmp = (Element)malloc(sizeof(ListNode));if (NULL == tmp){printf("malloc error\n");return;}L = HashTable->Thelists[Hash(key, HashTable->TableSize)];tmp->data = value;tmp->key = key;tmp->next = L->next;L->next = tmp;}elseprintf("the key alreadye xist\n");
}/*哈希表删除元素，元素为键值对*/
void Delete(HashTable* HashTable, int key)
{Element e = NULL, last = NULL;List L = NULL;int i = Hash(key, HashTable->TableSize);L = HashTable->Thelists[i];last = L;e = L->next;while (e != NULL && e->key != key) {last = e;e = e->next;}if (e) {//如果键值对存在last->next = e->next;delete(e);}
}/*哈希表元素中提取数据*/
void* Retrieve(Element e)
{return e ? e->data : NULL;
}/*销毁哈希表*/
void Destory(HashTable* HashTable)
{int i = 0;List L = NULL;Element cur = NULL, next = NULL;for (i = 0; i < HashTable->TableSize; i++){L = HashTable->Thelists[i];cur = L->next;while (cur != NULL){next = cur->next;free(cur);cur = next;}free(L);}free(HashTable->Thelists);free(HashTable);
}void main(void)
{const char*  elems[] = { "催化","小芳","苍老师"};int i = 0;HashTable* HashTable;HashTable = InitHash(31);Insert(HashTable, 1, (char*)(elems[0]));Insert(HashTable, 2, (char*)(elems[1]));Insert(HashTable, 3, const_cast<char*>(elems[2]));Delete(HashTable, 1);for (i = 0; i < 4; i++) {Element e = Find(HashTable, i);if (e) {printf("%s\n", (char *)Retrieve(e));//cout << (string*)Retrieve(e) << endl;}else {printf("Notfound[key:%d]\n", i);}}system("pause");
}

运行结果：
在这里插入图片描述

二、图

2.1 图的原理精讲

2.2 图的算法实现

2.2.1 结构体定义

#include <bits/stdc++.h>using namespace std;#define MaxSize 1024// 与节点连接的边的定义
typedef struct _EdgeNode {int adjvex;  // 领接的顶点int weight;  // 边的权重struct _EdgeNode* next;  // 下一条边
}EdgeNode;// 顶点节点
typedef struct _VertexNode {char data; // 节点数据struct _EdgeNode* first;  // 指向邻接的第一条边
}VertexNode,AdjList;// 定义邻接表
typedef struct _AdjListGraph {AdjList*  adjlist;   int vex; // 顶点数int edge;// 边数
}AdjListGraph;

2.2.2 初始化创建图

// 图的初始化
void Init(AdjListGraph& G) {G.adjlist = new AdjList[MaxSize]; // 属于直接创建最大值链表数量G.vex = 0;G.edge = 0;
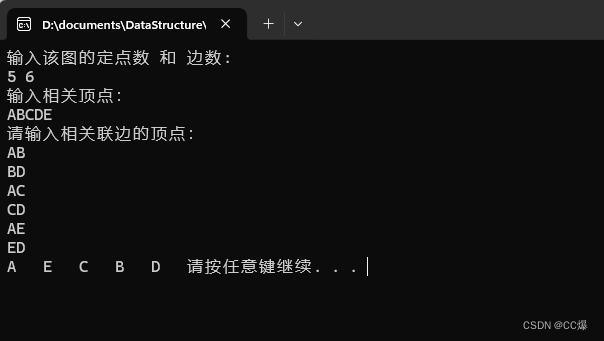
}// 图的创建
void Great(AdjListGraph& G) {cout << "输入该图的定点数 和 边数: " << endl;cin >> G.vex >> G.edge;cout << "输入相关顶点： " << endl;for (int i = 0; i < G.vex; i++) {cin >> G.adjlist[i].data;G.adjlist[i].first = NULL;}char v1 = 0, v2 = 0; //保存输入顶点的字符int i1, i2;	// 保存顶点在数组中的下标cout << "请输入相关联边的顶点：" << endl;for (int i = 0; i < G.edge; i++) {cin >> v1 >> v2;   // 代表 v1 v2 之间是相互连接的i1 = Location(G, v1);	 // 查找 v1 这个点下标在哪里i2 = Location(G, v2);if (i1 != -1 && i2 != -1) { // 代表两个点都找到了EdgeNode* temp = new EdgeNode;temp->adjvex = i2;      // 代表，1可以找到2，所以1可以访问到2的链表temp->next = G.adjlist[i1].first;  // 头插法G.adjlist[i1].first = temp;}}}// 通过顶点对应的字符寻找顶点在图中的领接点
// 用来查找这个点在图的下标是多少
int Location(AdjListGraph& G, char v) {for (int i = 0; i < G.vex; i++) {if (G.adjlist[i].data == v){return i;}}return -1;
}

2.3 深度优先遍历

思想：
1 首先以一个未被访问过的顶点作为起始顶点，沿当前顶点的边走到未访问过的顶点；
2 当没有未访问过的顶点时，则回到上一个顶点，继续试探别的顶点，直到所有的顶点都被访问过。

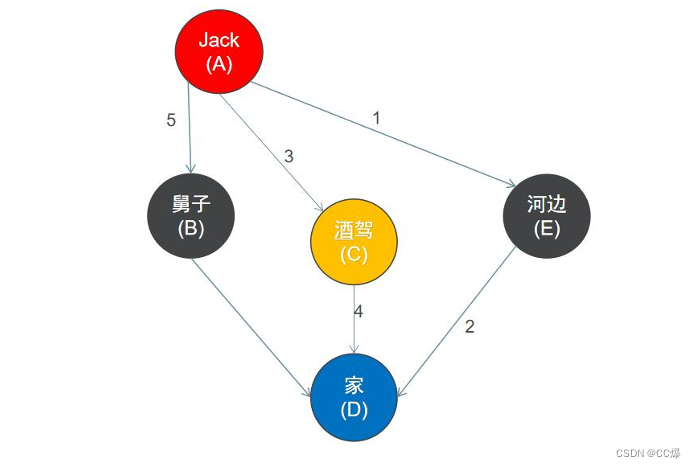
具体过程：
1. 首先从一个未走到过的顶点作为起始顶点，比如A顶点作为起点。
2. 沿A顶点的边去尝试访问其它未走到过的顶点，首先发现E号顶点还没有走到过，于是访问E顶点。
3. 再以E顶点作为出发点继续尝试访问其它未走到过的顶点，接下来访问D顶点。
4. 再尝试以D顶点作为出发点继续尝试访问其它未走到过的顶点。
5. 但是，此时沿D顶点的边，已经不能访问到其它未走到过的顶点，接下来返回到E顶点。
6. 返回到E顶点后，发现沿E顶点的边也不能再访问到其它未走到过的顶点。此时又回到顶点A（D->E->A），再以A顶点作为出发点继续访问其它未走到过的顶点，于是接下来访问C顶点。
7. 。。。。。。。。。。
8. 最终访问的结果是 A->E->D->C->B（这个不唯一的，看自己怎么选择路径）

// 对图上的一个顶点进行深度遍历 DFS
void DFS(AdjListGraph& G, int v) {int next = -1;if (visited[v]) { // 代表这个节点被访问过return;}cout << "节点未被访问过：" << G.adjlist[v].data;visited[v] = true;  // 设置为已访问；EdgeNode* temp = G.adjlist[v].first;//if (temp != NULL) { // 访问下一个节点//	next = temp->adjvex;//	if (visited[next] == false) {//		DFS(G, next);//	}//	while (temp->next) {//		temp = temp->next;//		next = temp->adjvex;//		if (visited[next] == false) {//			DFS(G, next);//		}//	}//}// 直接整合为一步解决while (temp) {next = temp->adjvex;temp = temp->next;if (visited[next] == false) {DFS(G, next);}}
}// 所有顶点遍历
void DFS_Main(AdjListGraph& G) {for (int i =0; i < G.vex; i++) {if (visited[i] == false) {DFS(G, i);}}
}

2.3 广度优先遍历

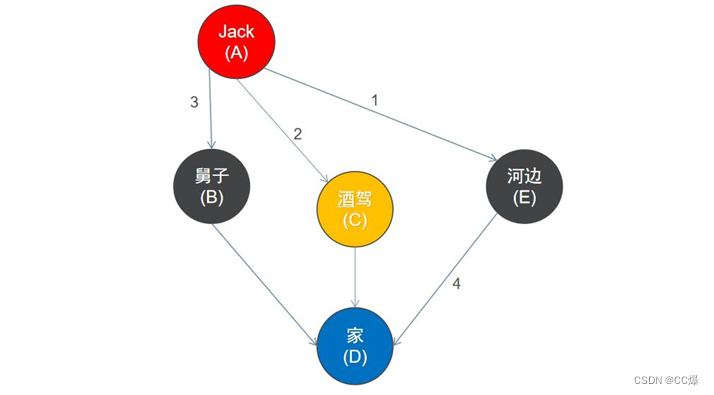
思想：
1 首先以一个未被访问过的顶点作为起始顶点，访问其所有相邻的顶点;
2 然后对每个相邻的顶点，再访问它们相邻的未被访问过的顶点，直到所有顶点都被访问过，遍历结束。
在这里插入图片描述

// 对一个顶点进行BFS
void BFS(AdjListGraph& G,int v) {queue<int> q;int cur = -1;  // 当前处理节点int index = -1; // 位置q.push(v); // 入队while (!q.empty()) { // 队列非空cur = q.front(); // 取队列头元素if (visited[cur] == false) { // 当前节点未访问cout << G.adjlist[cur].data << "   ";visited[cur] = true;}q.pop(); // 队头出队，因为已经访问过了EdgeNode* temp = G.adjlist[cur].first;while (temp != NULL){index = temp->adjvex;temp = temp->next;q.push(index);}}
}// 所有顶点遍历广度优先遍历
void BFS_Main(AdjListGraph& G) {for (int i = 0; i < G.vex; i++) {if (visited[i] == false) {BFS(G, i);}}
}

在这里插入图片描述

2.4 最短路径算法

从起点开始访问所有路径，则到达终点节点的路径有多条，其中路径权值最短的一条则为最短路径。
最短路径算法: 深度优先遍历、广度优先遍历、Bellman-Ford算法、弗洛伊德算法SPFA(ShortestPathFasterAlgorithm)算法和迪杰斯特拉算法等。
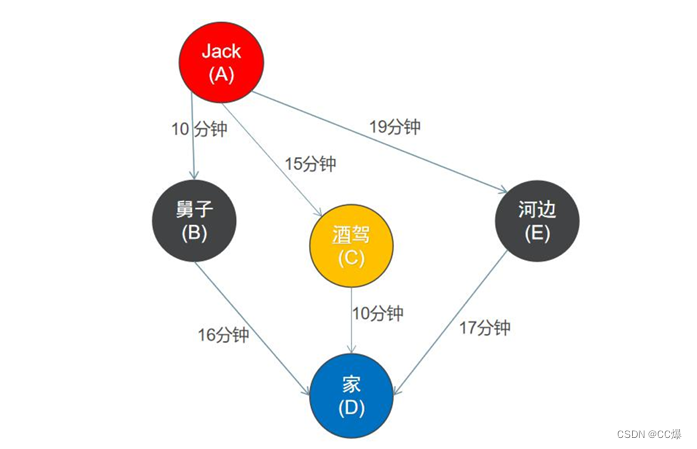
在这里插入图片描述
此处时间就相当于权重，我们采用 DFS 搜索算法进行最短路搜索：
此处，和之前写的DFS遍历，就在其基础上引入了权重.
最重要一点：就是回溯 ，因为我们遍历也需要保存路径，需要将每条路就过一遍，就存在，或许有的节点再另一条路劲可能访问过了，就需要回退，设置为未访问。

以下为搜索的主要代码：

int min_weights = 0x7FFFFFFF;  // 默认最大
int steps = 0; // 已走过的步数
int path[MaxSize] = { 0 };  // 保存走过的路径
int short_path[MaxSize] = {0};  // 保存最短路劲// 通过深度遍历，求解起点到终点最短路
void DFS(AdjListGraph& G,int start,int end, int weights) { int cur = -1;  // 用来查看当前下标if (start == end) { // 代表已经找到终点，不用继续遍历了for (int i = 0; i < steps; i++) {cout << G.adjlist[path[i]].data << "  "; // 可能的路径}cout << endl;cout << "权重:  " <<weights << endl;if (min_weights > weights) {min_weights = weights;memcpy(short_path, path, steps*sizeof(int));}}visited[start] = true; // 设置为已访问EdgeNode* temp = G.adjlist[start].first;while (temp) {int weight = temp->weight;  // 权重cur = temp->adjvex;  // 当前下标// 防止转圈,防止进入环if (visited[cur] == false) { visited[cur] = true;  // 当前点已访问path[steps++] = temp->adjvex;  // 保存路径到path数组DFS(G, cur, end, weights + weight);// 前一步探索完成后，让cur顶点为未选择状态，以便后续节点还可以访问 visited[cur] = false;  // 回溯path[--steps] = 0;}temp = temp->next;}
}

完整代码：

#include <bits/stdc++.h>using namespace std;#define MaxSize 1024// 与节点连接的边的定义
typedef struct _EdgeNode {int adjvex;  // 领接的顶点int weight;  // 边的权重struct _EdgeNode* next;  // 下一条边
}EdgeNode;// 顶点节点
typedef struct _VertexNode {char data; // 节点数据struct _EdgeNode* first;  // 指向邻接的第一条边
}VertexNode, AdjList;// 定义邻接表
typedef struct _AdjListGraph {AdjList* adjlist;   //int vex; // 顶点数int edge;// 边数
}AdjListGraph;bool visited[MaxSize]; //全局数组，用来记录节点是否已被访问int Location(AdjListGraph& G, char v);// 图的初始化
void Init(AdjListGraph& G) {G.adjlist = new AdjList[MaxSize]; // 属于直接创建最大值链表数量G.vex = 0;G.edge = 0;
}// 图的创建
void Great(AdjListGraph& G) {cout << "输入该图的定点数 和 边数: " << endl;cin >> G.vex >> G.edge;cout << "输入相关顶点： " << endl;for (int i = 0; i < G.vex; i++) {cin >> G.adjlist[i].data;G.adjlist[i].first = NULL;}char v1 = 0, v2 = 0; //保存输入顶点的字符int i1, i2;	// 保存顶点在数组中的下标int weight = 0 ;  // 保存边的权重cout << "请输入相关联边的顶点：" << endl;for (int i = 0; i < G.edge; i++) {cin >> v1 >> v2 >> weight;   // 代表 v1 v2 之间是相互连接的,和这个边权重i1 = Location(G, v1);	 // 查找 v1 这个点下标在哪里i2 = Location(G, v2);if (i1 != -1 && i2 != -1) { // 代表两个点都找到了EdgeNode* temp = new EdgeNode;temp->weight = weight;temp->adjvex = i2;      // 代表，1可以找到2，所以1可以访问到2的链表temp->next = G.adjlist[i1].first;  // 头插法G.adjlist[i1].first = temp;}}}// 通过顶点对应的字符寻找顶点在图中的领接点
// 用来查找这个点在图的下标是多少
int Location(AdjListGraph& G, char v) {for (int i = 0; i < G.vex; i++) {if (G.adjlist[i].data == v){return i;}}return -1;
}int min_weights = 0x7FFFFFFF;  // 默认最大
int steps = 0; // 已走过的步数
int path[MaxSize] = { 0 };  // 保存走过的路径
int short_path[MaxSize] = {0};  // 保存最短路劲// 通过深度遍历，求解起点到终点最短路
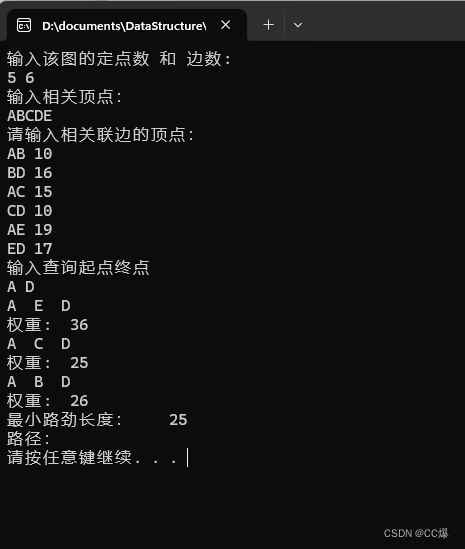
void DFS(AdjListGraph& G,int start,int end, int weights) { int cur = -1;  // 用来查看当前下标if (start == end) { // 代表已经找到终点，不用继续遍历了for (int i = 0; i < steps; i++) {cout << G.adjlist[path[i]].data << "  "; // 可能的路径}cout << endl;cout << "权重:  " <<weights << endl;if (min_weights > weights) {min_weights = weights;memcpy(short_path, path, steps*sizeof(int));}}visited[start] = true; // 设置为已访问EdgeNode* temp = G.adjlist[start].first;while (temp) {int weight = temp->weight;  // 权重cur = temp->adjvex;  // 当前下标// 防止转圈,防止进入环if (visited[cur] == false) { visited[cur] = true;  // 当前点已访问path[steps++] = temp->adjvex;  // 保存路径到path数组DFS(G, cur, end, weights + weight);// 前一步探索完成后，让cur顶点为未选择状态，以便后续节点还可以访问 visited[cur] = false;  // 回溯path[--steps] = 0;}temp = temp->next;}}int main() {AdjListGraph G;// 初始化Init(G);//创建图Great(G);// 深度遍历char start, end;cout << "输入查询起点终点" << endl;cin >> start >> end;// 求两点间的最短路径path[steps++] = Location(G, start);DFS(G, Location(G, start), Location(G, end), 0);cout << "最小路劲长度：    " << min_weights << endl;cout << "路径：";int i = 0;while (i < MaxSize && short_path[i]) {cout << G.adjlist[short_path[i]].data << "   ";i++;}cout << endl;system("pause");return 0;}

测试结果：
在这里插入图片描述

2.5 图的项目案例 (A* 算法)（非常重要）

2.5.1 A*算法原理

什么是A* 算法？

A算法较之传统的路径规划算法,实时性更高、灵活性更强,寻路结果更加接近人工选择的路径结果. A寻路算法并不是找到最优路径，只是找到相对近的路径，因为找最优要把所有可行路径都找出来进行对比，消耗性能太大，寻路效果只要相对近路径就行了*

寻路步骤

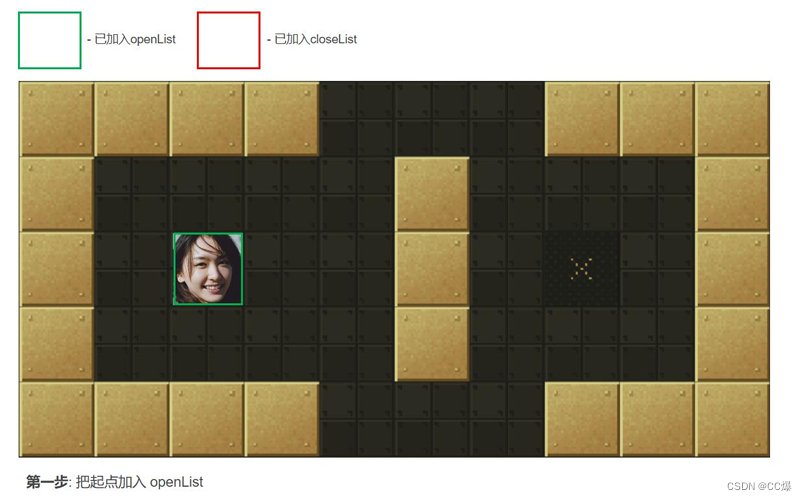
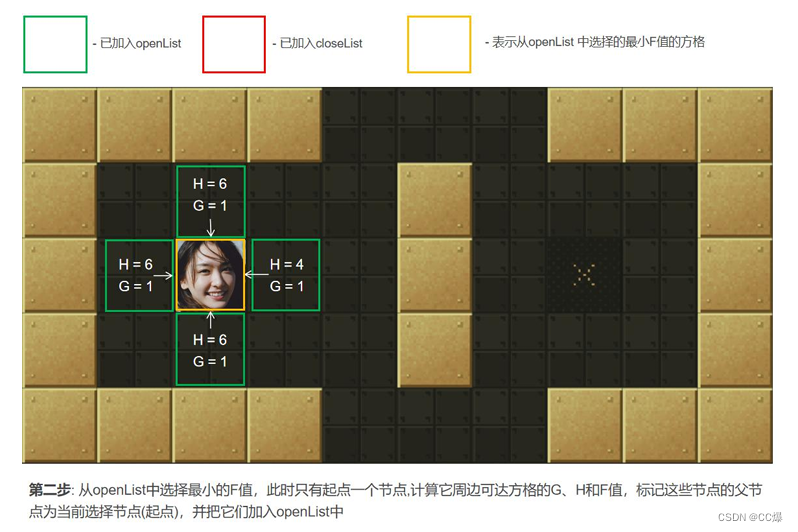
从起点开始, 把它作为待处理的方格存入一个预测可达的节点列表，简称openList, 即把起点放入“预测可达节点列表”，
可达节点列表openList就是一个等待检查方格的列表。
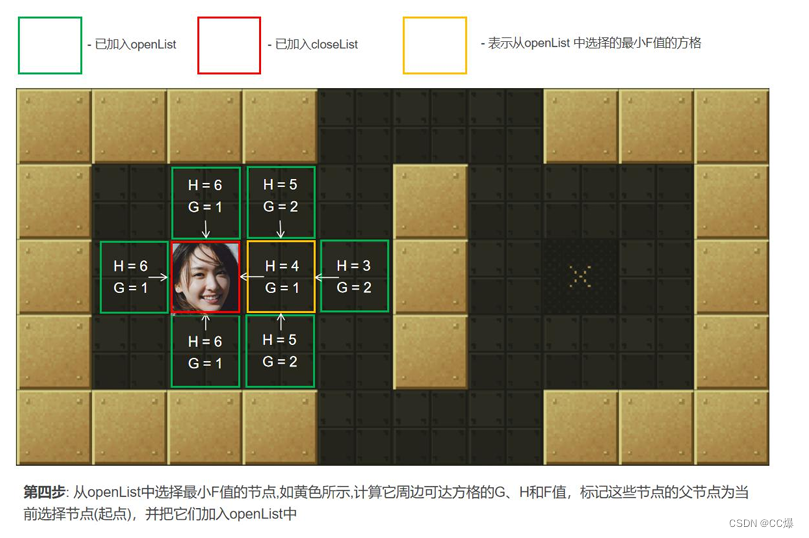
寻找openList中F值最小的点min（一开始只有起点）周围可以到达的方格（可到达的意思是其不是障碍物，也不存
在关闭列表中的方格,即不是已走过的方格）。计算min周围可到达的方格的F值。将还没在openList中点放入其中, 并
设置它们的"父方格"为点min,表示他们的上一步是经过min到达的。如果min下一步某个可到达的方格已经在openList
列表那么并且经min点它的F值更优,则修改F值并把其"父方格"设为点min。
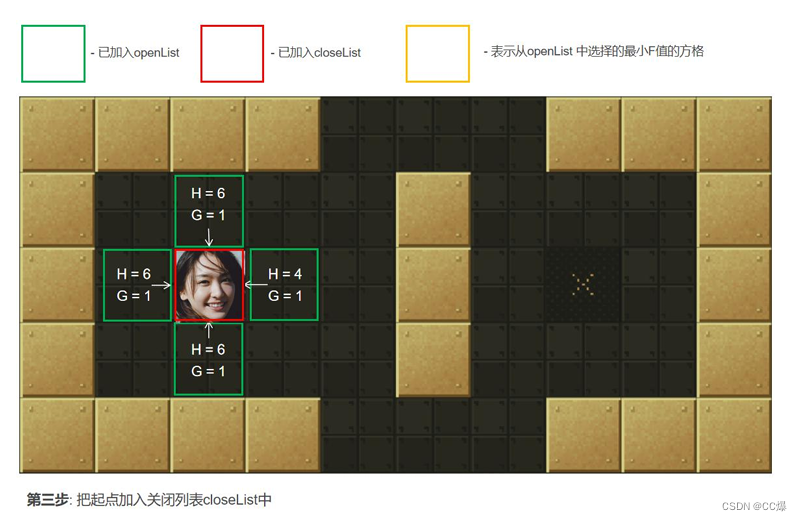
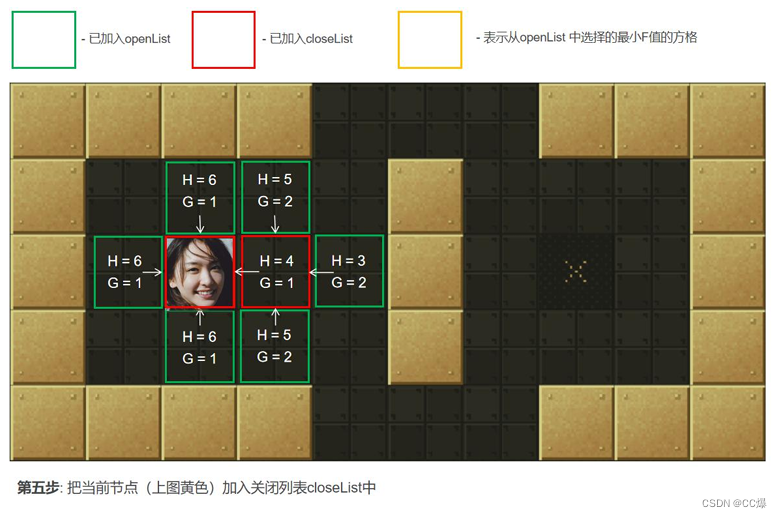
把2中的点min从"开启列表"中删除并存入"关闭列表"closeList中,closeList中存放的都是不需要再次检查的方格。如
果2中点min不是终点并且开启列表的数量大于零，那么继续从第2步开始。如果是终点执行第4步，如果openList列
表数量为零，那么就是找不到有效路径。
如果第3步中min 是终点，则结束查找，直接追溯父节点到起点的路径即为所选路径。

2.5.2 A*算法图示，一步一步讲解

具体寻路步步骤图示
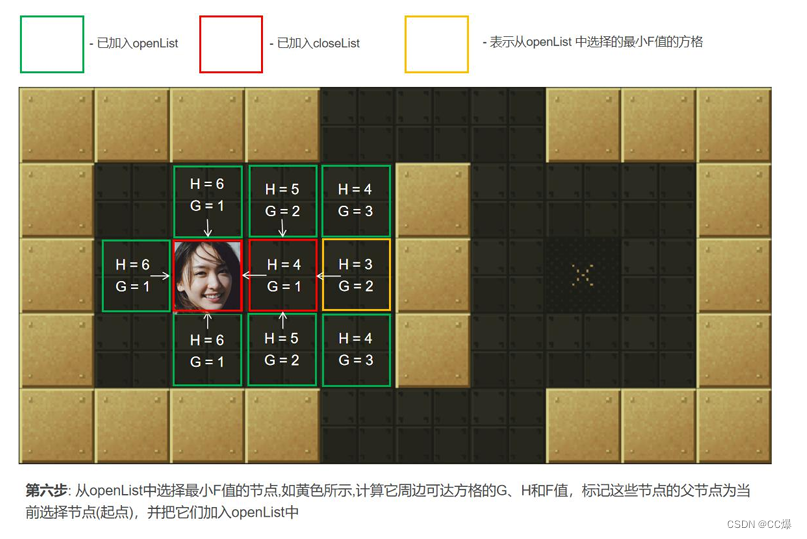
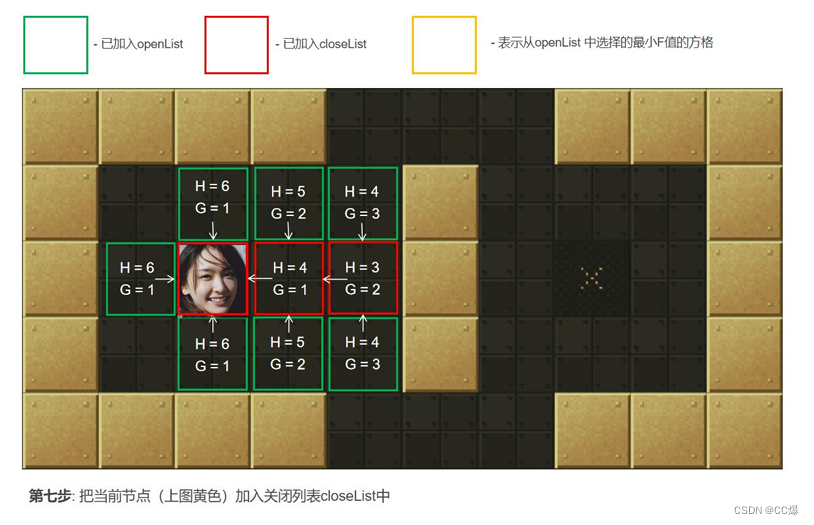
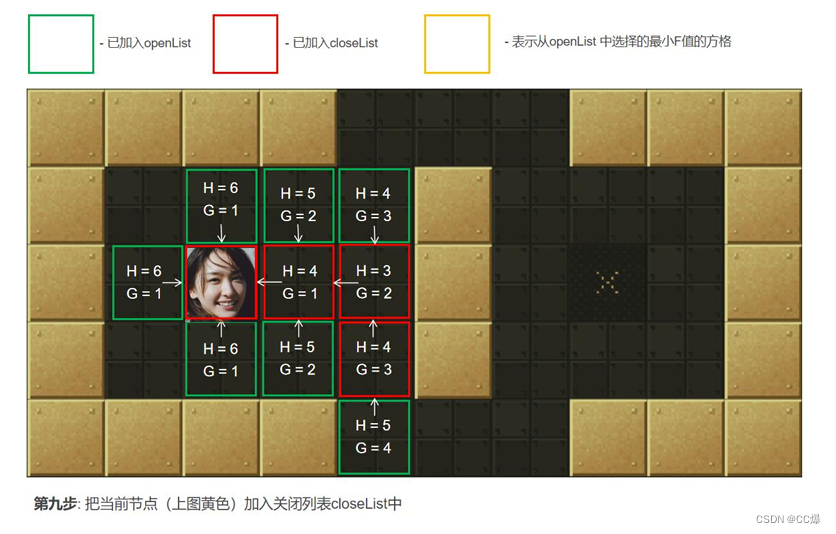
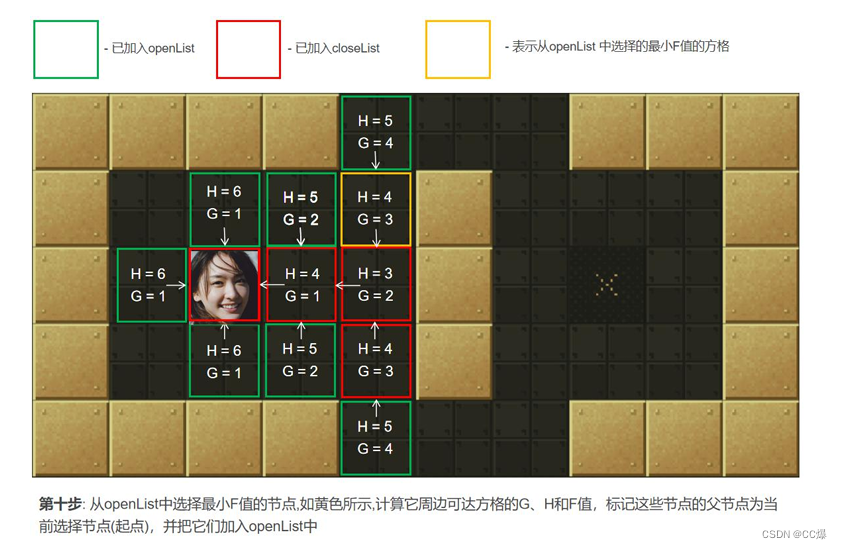
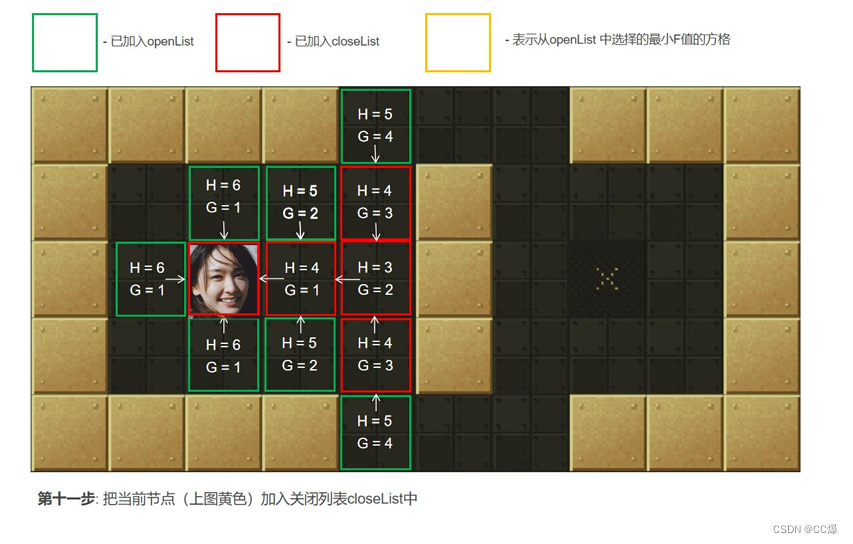
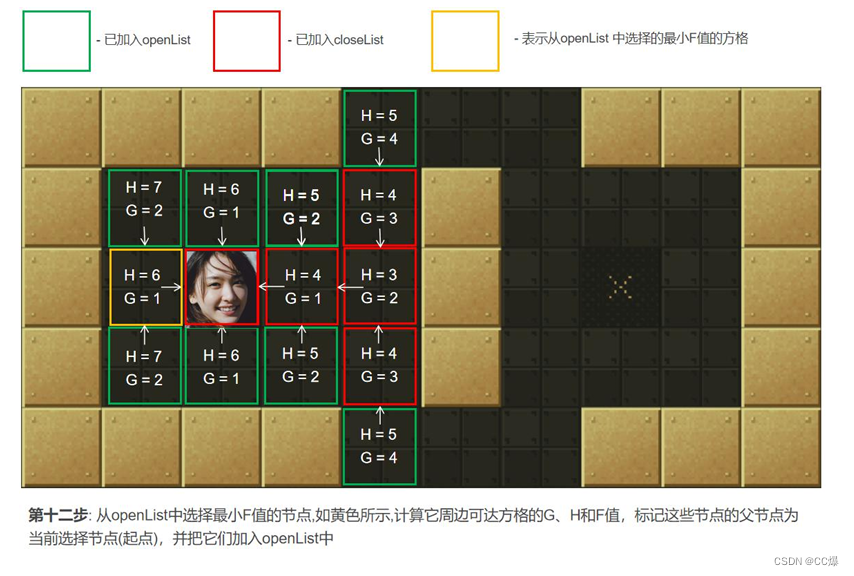
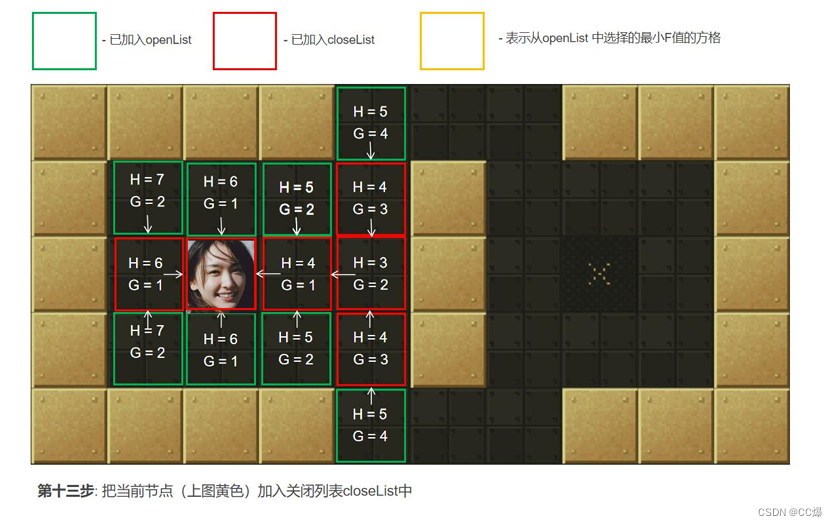
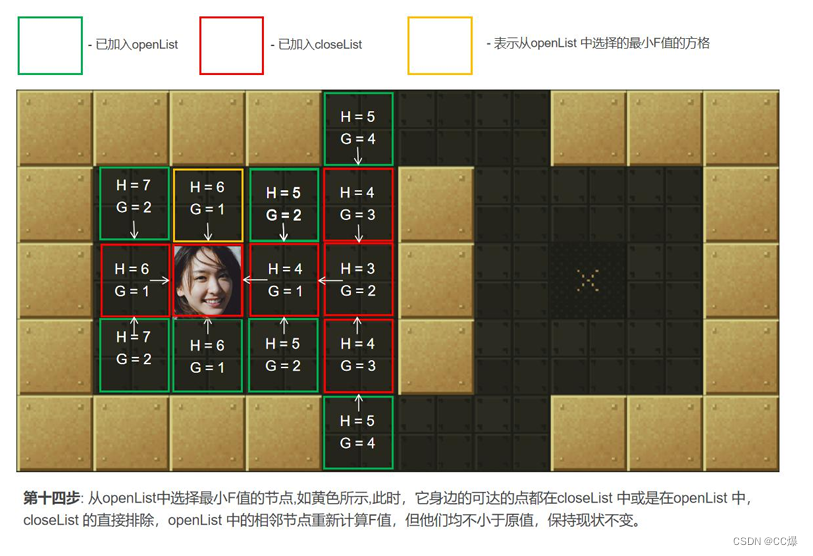
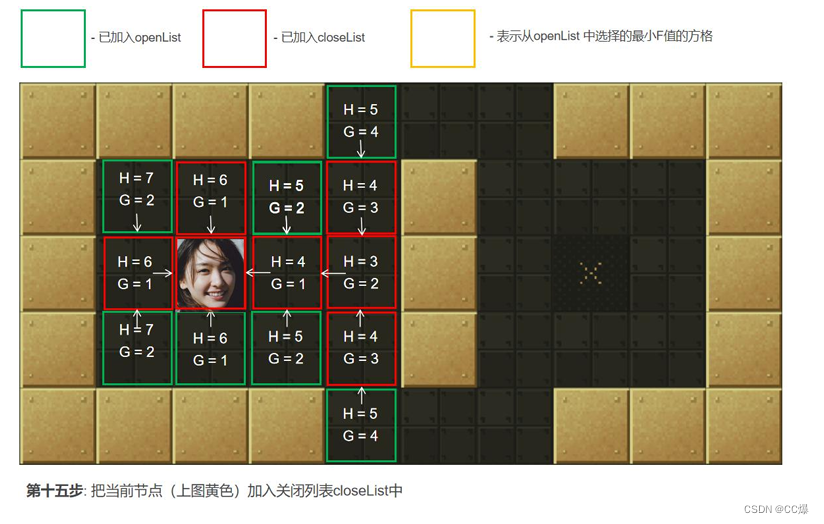
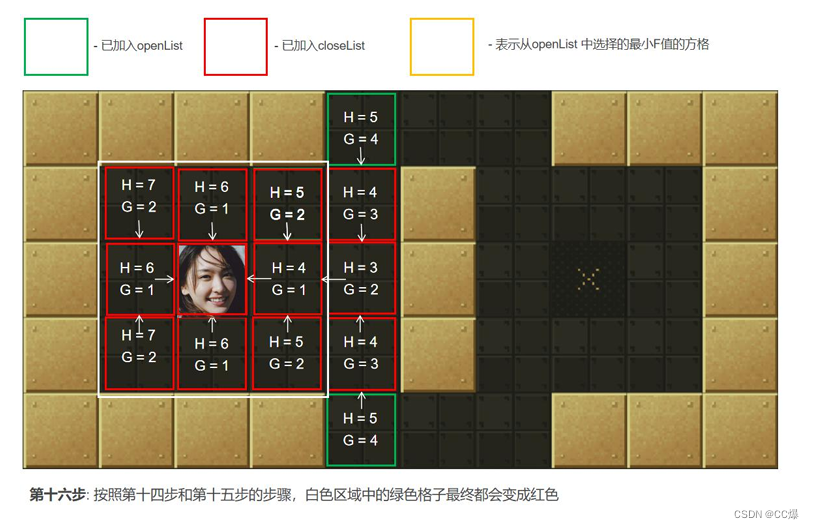
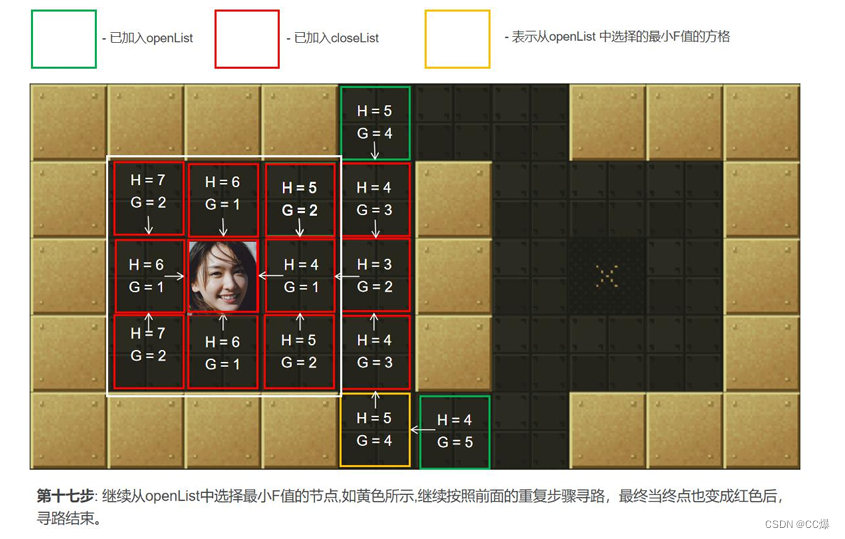
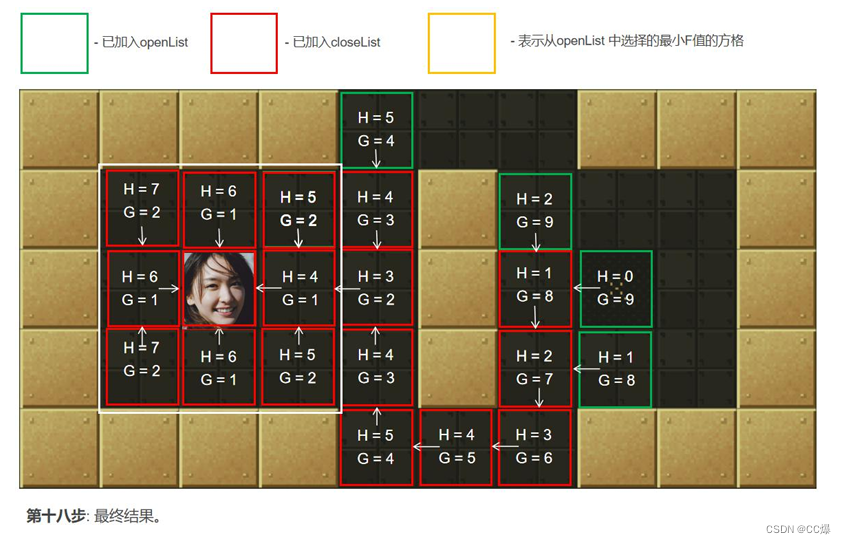
在这里插入图片描述

2.5.3 A*算法完整代码

AStar.h

// AStar.h#pragma once#include <list>
#include <vector>using namespace std;const int kCost1 = 10; // 直移一个消耗
const int kCost2 = 20; // 斜移一个消耗typedef struct _point {int x, y;		// 点坐标，x为横，y为竖int F, G, H;	// F= G+H ， 代表到终点总距离struct _point* parent;	// parent 坐标
}point;/* 分配一个节点（格子） */
point* AllocPoint(int x, int y);/* 初始化地图 */
void InitAstarMaze(int* _maze, int _lines, int _colums);/* 通过A*算法寻找路径 */
list<point*>GetPath(point* startPoint, point* endPoint);/* 清理资源、结束后调用 */
void ClearAstarMaze();

AStar.cpp

// AStar.cpp#include<bits/stdc++.h>
#include"AStar.h"static int* maze;	//迷宫对应二维数组，一维指针表示
static int cols;  // 二维数组对应列数
static int lines; // 二维数组对应行数static list<point*> openList;	//	开放列表
static list<point*> closeList;	//	关闭列表/* 搜索从起点到终点的最佳路径 */
static point* findPath(point* startPoint, point* endPoint);/* 从openList里面获取最小的节点 */
static point* getLeastPoint();	/* 获取当前节点的周边节点 */
static vector<point*> getSurroundPoints(const point* curPoint);/* 判断某点是否可以用于下一步判断 */
static bool isCanreach(const point* curPoint, point* temp);/* 判断开启/关闭列表中是否包含某点 */
static point* isInList(const std::list<point*>& list, const point* cpoint);//计算FGH值
static int calG(point* temp_start, point* point);
static int calH(point* cpoint, point* end);
static int calF(point* cpoint);/* 分配一个节点（格子） */
point* AllocPoint(int x, int y) {point* temp = new point;memset(temp, 0, sizeof(point));  // 初始值清0temp->x = x;temp->y = y;return temp;
}/* 初始化地图 */
void InitAstarMaze(int* _maze, int _lines, int _colums) {maze = _maze;lines = _lines;cols = _colums;
}/* 通过A*算法寻找路径 */
list<point*> GetPath(point* startPoint, point* endPoint) {point* result = findPath(startPoint, endPoint);list<point*> path; // 返回的路径// 如果没找到路径，则返回空的列表while (result) {path.push_front(result);result = result->parent;   // 相当于最后一个节点逆转，比如原本path 是 CBA,逆转为ABC}return path;  
}/* 搜索从起点到终点的最佳路径 */
static point* findPath(point* startPoint, point* endPoint) {// 1. 初始节点放入 OpenListopenList.push_back(AllocPoint(startPoint->x,startPoint->y));while (!openList.empty()) {// 2. 寻找openList中最小值point* curPoint = getLeastPoint(); // 取到最小初始值// 3. 把当前节点放在关闭列表中openList.remove(curPoint);closeList.push_back(curPoint);// 4. 找到当前节点可到达的周围节点，并计算F值vector<point*> surroundPoints = getSurroundPoints(curPoint);vector<point*>::const_iterator it;for (it = surroundPoints.begin(); it != surroundPoints.end(); it++) {point* target = *it;// 对某个格子，如果它不在开放列表中，加入到开启列表，设置当前格为其父节点，计算FGHpoint* exist = isInList(openList, target);if (!exist) {target->parent = curPoint;target->G = calG(curPoint, target);target->H = calH(target, endPoint);target->F = calF(target);openList.push_back(target);}// 如果已经存在，就从新计算G值,然后看大小更新else {int tempG = calG(curPoint, target);if (tempG < target->G) {exist->parent = curPoint;exist->G = tempG;exist->F = calF(target);}delete target;}}// 结束条件surroundPoints.clear();point* resPoint = isInList(openList, endPoint); // end 已经在openList，代表已经跑到终点if (resPoint) {return resPoint;}}return NULL;
}/* 从openList里面获取最小的节点 */
static point* getLeastPoint() {if (!openList.empty()) {point* resPoint = openList.front();list<point* >::const_iterator it;  // 迭代器for (it = openList.begin(); it != openList.end(); it++) {point* p = *it;  // 如何获取迭代器数据？ 加 *if (p->F < resPoint->F) {resPoint = *it;}}return resPoint;}return NULL;
}/* 获取当前节点的周边节点 */
static vector<point*> getSurroundPoints(const point* curPoint) {vector<point* > surroundPoints;for (int x = curPoint->x - 1; x <= curPoint->x + 1; x++) {for (int y = curPoint->y - 1; y <= curPoint->y + 1; y++) { // 周围8个点point* temp = AllocPoint(x, y);if (isCanreach(curPoint, temp)) { // 只需要 8个点中的上下左右，斜角此处不考虑surroundPoints.push_back(temp);}else {delete temp;}}}return surroundPoints;
}/* 判断某点是否可以用于下一步判断 */
static bool isCanreach(const point* curPoint, point* temp) { // curPoint 当前点，temp 下一个点if (temp->x<0 || temp->x>(lines - 1)         // x超过范围|| temp->y<0 || temp->y>(cols - 1)		// y超过范围|| maze[temp->x * cols + temp->y] == 1  // 障碍物|| maze[temp->x * cols + temp->y] == 2  // 障碍物|| (temp->x == curPoint->x && temp->y == curPoint->y) // 点从重叠|| isInList(closeList, temp)) {return false;}// abs 求绝对值if (abs(curPoint->x - temp->x) + abs(curPoint->y - temp->y) == 1) {return true;}else {return false;}
}/* 判断开启/关闭列表中是否包含某点 */
static point* isInList(const std::list<point*>& list, const point* cpoint){//判断某个节点是否在列表中，这里不能比较指针，因为每次加入列表是新开辟的节点，只能比较坐标std::list<point*>::const_iterator itor;for (itor = list.begin(); itor != list.end(); itor++) {if ((*itor)->x == cpoint->x && (*itor)->y == cpoint->y) {return *itor;}}return NULL;
}//计算FGH值
static int calG(point* temp_start, point* cpoint)
{// 判断走直线还是斜线，此题只需要直线，斜线以后可以这么写int extraG = (abs(cpoint->x - temp_start->x) + abs(cpoint->y - temp_start->y)) == 1 ? kCost1 : kCost2;int parentG = (cpoint->parent == NULL ? NULL : cpoint->parent->G); //如果是初始节点，则其父节点是空return parentG + extraG;
}
static int calH(point* cpoint, point* end) {// 就是该点到终点，看成一个矩形，我们就看直线距离，这个看自己怎么算，都可以return (int)sqrt((double)(end->x - cpoint->x) * (double)(end->x - cpoint->x) +(double)(end->y - cpoint->y) * (double)(end->y - cpoint->y));
}
static int calF(point* cpoint) {return cpoint->G + cpoint->H;
}/* 清理资源、结束后调用 */
void ClearAstarMaze() {maze = NULL;lines = 0;cols = 0;std::list<point *>::iterator itor;//清除openList中的元素cout << openList.size() << endl;for (itor = openList.begin(); itor != openList.end();) {delete* itor;itor = openList.erase(itor);// 获取到下一个节点}//清理closeList中的元素cout << closeList.size() << endl;for (itor = closeList.begin(); itor != closeList.end();) {delete* itor;itor = closeList.erase(itor);}
}

main.cpp

// main.cpp#include "AStar.h"
#include<bits/stdc++.h>
#include<windows.h>using namespace std;const int ROWS = 13;
const int COLS = 13;//定义地图数组
int maps[13][13] = {//二维数组在内存顺序存储的{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,},{0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0,},{0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0,},{0, 1, 0, 1, 0, 1, 2, 1, 0, 1, 0, 1, 0,},{0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0,},{0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0,},{0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0,},{2, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 2,},{0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0,},{0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0,},{0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0,},{0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0,},{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,}
};void PrintMap(int maps[ROWS][COLS]) {for (int i = 0; i < ROWS; ++i) {for (int j = 0; j < COLS; ++j) {if (maps[i][j] == 0) {std::cout << '0';  // 通路用空格表示}else {std::cout << '*';  // 墙用星号表示}}std::cout << '\n';}
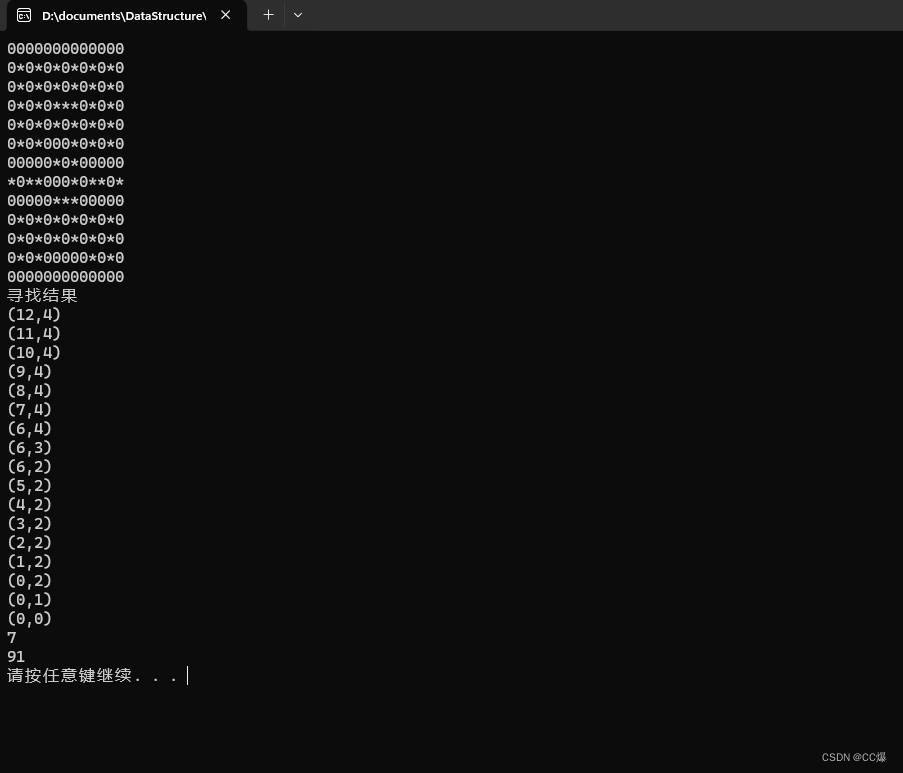
}void AStarText() {InitAstarMaze(&maps[0][0], 13, 13);PrintMap(maps);// 设置起始地址 和 终点point* start = AllocPoint(12, 4);point* end = AllocPoint(0, 0);// A* 算法寻找路劲list<point*> path = GetPath(start, end);cout << "寻找结果" << endl;list<point*>::const_iterator it;for (it = path.begin(); it != path.end(); it++) {point* cur = *it;cout << '(' << cur->x << ',' << cur->y << ')' << endl;//delete cur;//it = path.erase(it);Sleep(800);}ClearAstarMaze();
}int main() {AStarText();system("pause");return 0;
}