【机器学习】机器学习创建算法第6篇：线性回归,学习目标【附代码文档】

机器学习（算法篇）完整教程（附代码资料）主要内容讲述：机器学习算法课程定位、目标，K-近邻算法定位,目标,学习目标,1 什么是K-近邻算法,1 Scikit-learn工具介绍,2 K-近邻算法API。K-近邻算法，1.4 k值的选择学习目标,学习目标,1 kd树简介,2 构造方法,3 案例分析,4 总结。K-近邻算法，1.6 案例：鸢尾花种类预测--数据集介绍学习目标,1 案例：鸢尾花种类预测,2 scikit-learn中数据集介绍,1 什么是特征预处理,2 归一化,3 标准化。K-近邻算法，1.8 案例：鸢尾花种类预测—流程实现学习目标,1 再识K-近邻算法API,2 案例：鸢尾花种类预测,总结,1 什么是交叉验证(cross validation),2 什么是网格搜索(Grid Search)。线性回归，2.1 线性回归简介学习目标,1 线性回归应用场景,2 什么是线性回归,1 线性回归API,2 举例,1 常见函数的导数。线性回归，2.6 梯度下降法介绍学习目标,1 全梯度下降算法（FG）,2 随机梯度下降算法（SG）,3 小批量梯度下降算法（mini-bantch）,4 随机平均梯度下降算法（SAG）,5 算法比较。线性回归，2.8 欠拟合和过拟合学习目标,1 定义,2 原因以及解决办法,3 正则化,4 维灾难【拓展知识】。线性回归，2.9 正则化线性模型学习目标,1 Ridge Regression (岭回归，又名 Tikhonov regularization),2 Lasso Regression(Lasso 回归),3 Elastic Net (弹性网络),4 Early Stopping [了解],1 API。逻辑回归，3.4 分类评估方法学习目标,1.分类评估方法,2 ROC曲线与AUC指标,3 总结,1 曲线绘制,2 意义解释。决策树算法，4.4 特征工程-特征提取学习目标,1 特征提取,2 字典特征提取,3 文本特征提取。决策树算法，4.5 决策树算法api学习目标,1 泰坦尼克号数据,2 步骤分析,3 代码过程,3 决策树可视化,学习目标。集成学习，5.3 Boosting学习目标,1.boosting集成原理,2 GBDT(了解),3.XGBoost【了解】,4 什么是泰勒展开式【拓展】,学习目标。聚类算法，6.4 模型评估学习目标,1 误差平方和(SSE \The sum of squares due to error)：,2 “肘”方法 (Elbow method) — K值确定,3 轮廓系数法（Silhouette Coefficient）,4 CH系数（Calinski-Harabasz Index）,5 总结。聚类算法，6.6 特征降维学习目标,1 降维,2 特征选择,3 主成分分析,1 需求,2 分析。

全套笔记资料代码移步： 前往gitee仓库查看

感兴趣的小伙伴可以自取哦，欢迎大家点赞转发~

全套教程部分目录：

部分文件图片：

线性回归

学习目标

  • 掌握线性回归的实现过程
  • 应用LinearRegression或SGDRegressor实现回归预测
  • 知道回归算法的评估标准及其公式
  • 知道过拟合与欠拟合的原因以及解决方法
  • 知道岭回归的原理及与线性回归的不同之处
  • 应用Ridge实现回归预测
  • 应用joblib实现模型的保存与加载

2.6 梯度下降法介绍

上一节中给大家介绍了最基本的梯度下降法实现流程，常见的梯度下降算法有：

  • 全梯度下降算法(Full gradient descent），
  • 随机梯度下降算法（Stochastic gradient descent），
  • 随机平均梯度下降算法（Stochastic average gradient descent）
  • 小批量梯度下降算法（Mini-batch gradient descent）,

它们都是为了正确地调节权重向量，通过为每个权重计算一个梯度，从而更新权值，使目标函数尽可能最小化。其差别在于样本的使用方式不同。

1 全梯度下降算法（FG）

计算训练集所有样本误差，对其求和再取平均值作为目标函数。

权重向量沿其梯度相反的方向移动，从而使当前目标函数减少得最多。

因为在执行每次更新时，我们需要在整个数据集上计算所有的梯度，所以批梯度下降法的速度会很慢，同时，批梯度下降法无法处理超出内存容量限制的数据集。

批梯度下降法同样也不能在线更新模型，即在运行的过程中，不能增加新的样本。

其是在整个训练数据集上计算损失函数关于参数θ的梯度：

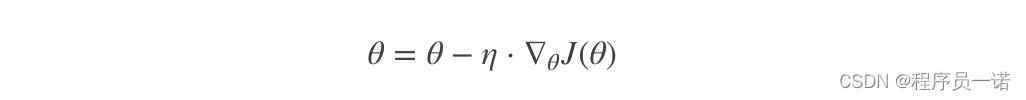
image-20190403165606134

2 随机梯度下降算法（SG）

由于FG每迭代更新一次权重都需要计算所有样本误差，而实际问题中经常有上亿的训练样本，故效率偏低，且容易陷入局部最优解，因此提出了随机梯度下降算法。

其每轮计算的目标函数不再是全体样本误差，而仅是单个样本误差，即每次只代入计算一个样本目标函数的梯度来更新权重，再取下一个样本重复此过程，直到损失函数值停止下降或损失函数值小于某个可以容忍的阈值。

此过程简单，高效，通常可以较好地避免更新迭代收敛到局部最优解。其迭代形式为

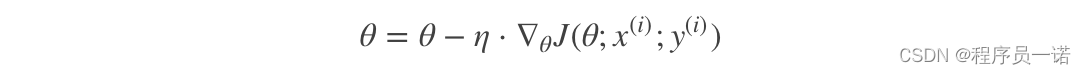
image-20190403165840513

每次只使用一个样本迭代，若遇上噪声则容易陷入局部最优解。

其中，x(i)表示一条训练样本的特征值，y(i)表示一条训练样本的标签值

但是由于，SG每次只使用一个样本迭代，若遇上噪声则容易陷入局部最优解。

3 小批量梯度下降算法（mini-bantch）

小批量梯度下降算法是FG和SG的折中方案,在一定程度上兼顾了以上两种方法的优点。

每次从训练样本集上随机抽取一个小样本集，在抽出来的小样本集上采用FG迭代更新权重。

被抽出的小样本集所含样本点的个数称为batch_size，通常设置为2的幂次方，更有利于GPU加速处理。

特别的，若batch_size=1，则变成了SG；若batch_size=n，则变成了FG.其迭代形式为

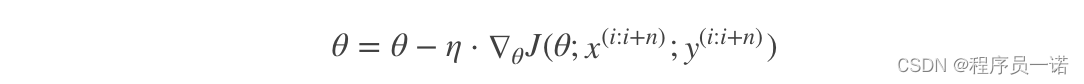
image-20190403170347851

4 随机平均梯度下降算法（SAG）

在SG方法中，虽然避开了运算成本大的问题，但对于大数据训练而言，SG效果常不尽如人意，因为每一轮梯度更新都完全与上一轮的数据和梯度无关。

随机平均梯度算法克服了这个问题，在内存中为每一个样本都维护一个旧的梯度，随机选择第i个样本来更新此样本的梯度，其他样本的梯度保持不变，然后求得所有梯度的平均值，进而更新了参数。

如此，每一轮更新仅需计算一个样本的梯度，计算成本等同于SG，但收敛速度快得多。

5 算法比较

为了比对四种基本梯度下降算法的性能，我们通过一个逻辑二分类实验来说明。本文所用的Adult数据集来自UCI公共数据库（[ 数据集共有15081条记录，包括“性别”“年龄”“受教育情况”“每周工作时常”等14个特征，数据标记列显示“年薪是否大于50000美元”。我们将数据集的80%作为训练集，剩下的20%作为测试集，使用逻辑回归建立预测模型，根据数据点的14个特征预测其数据标记（收入情况）。

以下6幅图反映了模型优化过程中四种梯度算法的性能差异。

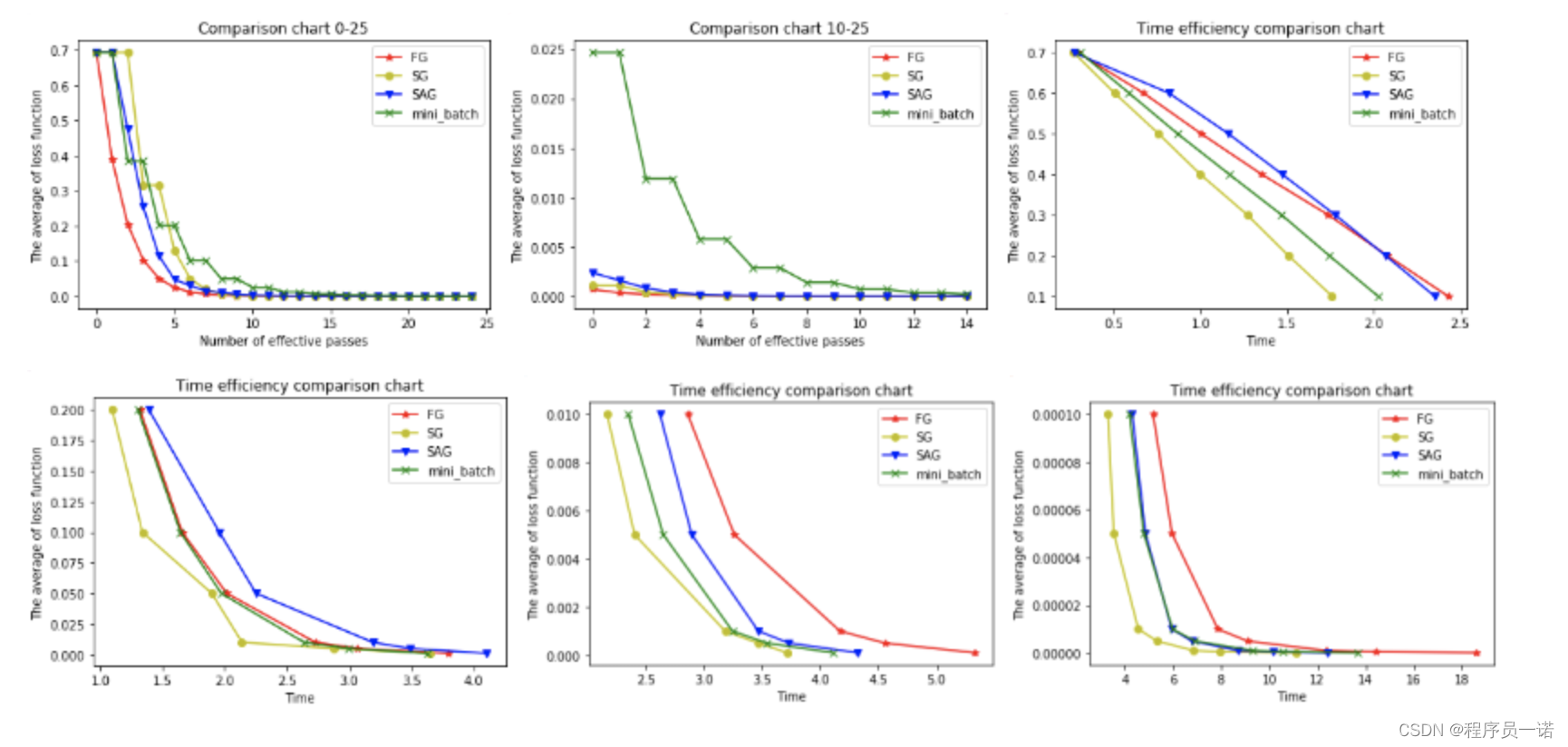
image-20190403173001750

在图1和图2中，横坐标代表有效迭代次数，纵坐标代表平均损失函数值。图1反映了前25次有效迭代过程中平均损失函数值的变化情况，为了便于观察，图2放大了第10次到25次的迭代情况。

从图1中可以看到，四种梯度算法下，平均损失函数值随迭代次数的增加而减少。FG的迭代效率始终领先，能在较少的迭代次数下取得较低的平均损失函数值。FG与SAG的图像较平滑，这是因为这两种算法在进行梯度更新时都结合了之前的梯度；SG与mini-batch的图像曲折明显，这是因为这两种算法在每轮更新梯度时都随机抽取一个或若干样本进行计算，并没有考虑到之前的梯度。

从图2中可以看到虽然四条折现的纵坐标虽然都趋近于0，但SG和FG较早，mini-batch最晚。这说明如果想使用mini-batch获得最优参数，必须对其进行较其他三种梯度算法更多频次的迭代。

在图3，4，5，6中，横坐标表示时间，纵坐标表示平均损失函数值。

从图3中可以看出使用四种算法将平均损失函数值从0.7降到0.1最多只需要2.5s，由于本文程序在初始化梯度时将梯度设为了零，故前期的优化效果格外明显。其中SG在前期的表现最好，仅1.75s便将损失函值降到了0.1，虽然SG无法像FG那样达到线性收敛，但在处理大规模机器学习问题时，为了节约时间成本和存储成本，可在训练的一开始先使用SG，后期考虑到收敛性和精度可改用其他算法。

从图4，5，6可以看出，随着平均损失函数值的不断减小，SG的性能逐渐反超FG，FG的优化效率最慢，即达到相同平均损失函数值时FG所需要的时间最久。

综合分析六幅图我们得出以下结论：

（1）FG方法由于它每轮更新都要使用全体数据集，故花费的时间成本最多，内存存储最大。

（2）SAG在训练初期表现不佳，优化速度较慢。这是因为我们常将初始梯度设为0，而SAG每轮梯度更新都结合了上一轮梯度值。

（3）综合考虑迭代次数和运行时间，SG表现性能都很好，能在训练初期快速摆脱初始梯度值，快速将平均损失函数降到很低。但要注意，在使用SG方法时要慎重选择步长，否则容易错过最优解。

（4）mini-batch结合了SG的“胆大”和FG的“心细”，从6幅图像来看，它的表现也正好居于SG和FG二者之间。在目前的机器学习领域，mini-batch是使用最多的梯度下降算法，正是因为它避开了FG运算效率低成本大和SG收敛效果不稳定的缺点。

6 梯度下降优化算法(拓展)

以下这些算法主要用于深度学习优化

  • 动量法

  • 其实动量法(SGD with monentum)就是SAG的姐妹版

  • SAG是对过去K次的梯度求平均值

  • SGD with monentum 是对过去所有的梯度求加权平均

  • Nesterov加速梯度下降法

  • 类似于一个智能球，在重新遇到斜率上升时候，能够知道减速

  • Adagrad

  • 让学习率使用参数

  • 对于出现次数较少的特征，我们对其采用更大的学习率，对于出现次数较多的特征，我们对其采用较小的学习率。

  • Adadelta

  • Adadelta是Adagrad的一种扩展算法，以处理Adagrad学习速率单调递减的问题。

  • RMSProp

  • 其结合了梯度平方的指数移动平均数来调节学习率的变化。

  • 能够在不稳定（Non-Stationary）的目标函数情况下进行很好地收敛。

  • Adam

  • 结合AdaGrad和RMSProp两种优化算法的优点。

  • 是一种自适应的学习率算法

参考链接：[

2.5 线性回归api再介绍

  • sklearn.linear_model.LinearRegression(fit_intercept=True)

  • 通过正规方程优化

  • fit_intercept：是否计算偏置
  • LinearRegression.coef_：回归系数

  • LinearRegression.intercept_：偏置

  • sklearn.linear_model.SGDRegressor(loss="squared_loss", fit_intercept=True, learning_rate ='invscaling', eta0=0.01)

  • SGDRegressor类实现了随机梯度下降学习，它支持不同的loss函数和正则化惩罚项来拟合线性回归模型。

  • loss:损失类型

    • loss=”squared_loss”: 普通最小二乘法

  • fit_intercept：是否计算偏置

  • learning_rate : string, optional

    • 学习率填充
    • 'constant': eta = eta0
    • 'optimal': eta = 1.0 / (alpha * (t + t0)) [default]

    • 'invscaling': eta = eta0 / pow(t, power_t)

      • power_t=0.25:存在父类当中

    • 对于一个常数值的学习率来说，可以使用learning_rate=’constant’ ，并使用eta0来指定学习率。

  • SGDRegressor.coef_：回归系数

  • SGDRegressor.intercept_：偏置

sklearn提供给我们两种实现的API， 可以根据选择使用

线性回归

学习目标

  • 掌握线性回归的实现过程
  • 应用LinearRegression或SGDRegressor实现回归预测
  • 知道回归算法的评估标准及其公式
  • 知道过拟合与欠拟合的原因以及解决方法
  • 知道岭回归的原理及与线性回归的不同之处
  • 应用Ridge实现回归预测
  • 应用joblib实现模型的保存与加载

2.7 案例：波士顿房价预测

  • 数据介绍

房ä"·æ•°æ®é›†ä"‹ç"

属性

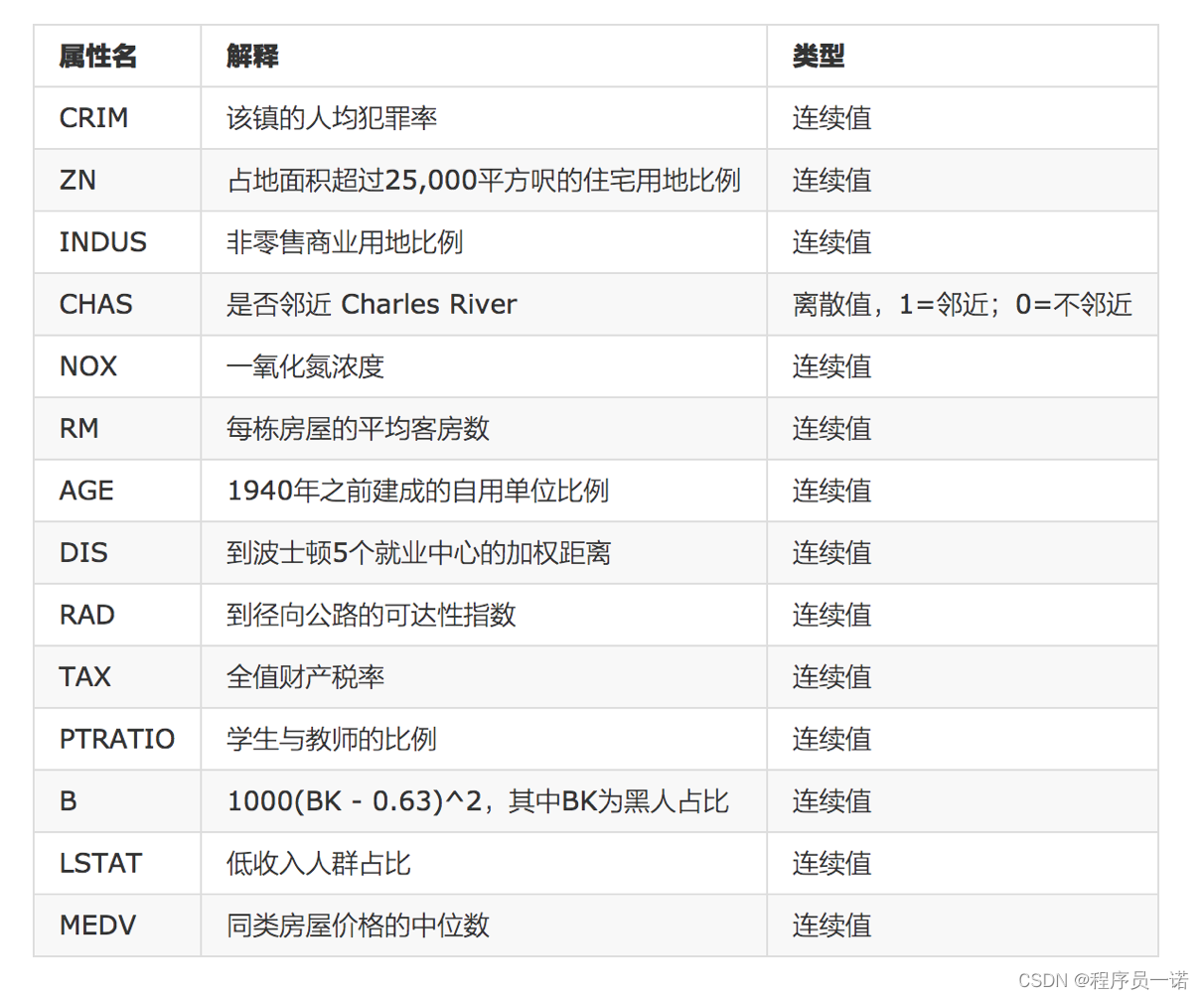
给定的这些特征，是专家们得出的影响房价的结果属性。我们此阶段不需要自己去探究特征是否有用，只需要使用这些特征。到后面量化很多特征需要我们自己去寻找

1 分析

回归当中的数据大小不一致，是否会导致结果影响较大。所以需要做标准化处理。

  • 数据分割与标准化处理
  • 回归预测
  • 线性回归的算法效果评估

2 回归性能评估

均方误差(Mean Squared Error)MSE)评价机制：

线性回归评估

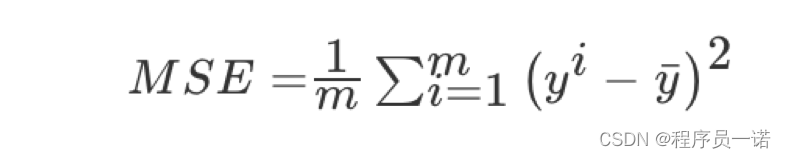
注：yi为预测值，¯y为真实值

  • sklearn.metrics.mean_squared_error(y_true, y_pred)

  • 均方误差回归损失

  • y_true:真实值
  • y_pred:预测值
  • return:浮点数结果

3 代码

def linear_model1():"""线性回归:正规方程:return:None"""# 1.获取数据data = load_boston()# 2.数据集划分x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)# 3.特征工程-标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.fit_transform(x_test)# 4.机器学习-线性回归(特征方程)estimator = LinearRegression()estimator.fit(x_train, y_train)# 5.模型评估# 5.1 获取系数等值y_predict = estimator.predict(x_test)print("预测值为:\n", y_predict)print("模型中的系数为:\n", estimator.coef_)print("模型中的偏置为:\n", estimator.intercept_)# 5.2 评价# 均方误差error = mean_squared_error(y_test, y_predict)print("误差为:\n", error)def linear_model2():"""线性回归:梯度下降法:return:None"""# 1.获取数据data = load_boston()# 2.数据集划分x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)# 3.特征工程-标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.fit_transform(x_test)# 4.机器学习-线性回归(特征方程)estimator = SGDRegressor(max_iter=1000)estimator.fit(x_train, y_train)# 5.模型评估# 5.1 获取系数等值y_predict = estimator.predict(x_test)print("预测值为:\n", y_predict)print("模型中的系数为:\n", estimator.coef_)print("模型中的偏置为:\n", estimator.intercept_)# 5.2 评价# 均方误差error = mean_squared_error(y_test, y_predict)print("误差为:\n", error)

我们也可以尝试去修改学习率

estimator = SGDRegressor(max_iter=1000,learning_rate="constant",eta0=0.1)

此时我们可以通过调参数，找到学习率效果更好的值。

未完待续， 同学们请等待下一期

全套笔记资料代码移步： 前往gitee仓库查看

感兴趣的小伙伴可以自取哦，欢迎大家点赞转发~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/818594.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

【七 （1）指标体系建设-构建高效的故障管理指标体系】

【七 （1）指标体系建设-构建高效的故障管理指标体系】

目录 文章导航一、故障概述1、故障：2、故障管理： 二、指标体系概述1、指标2、指标体系 三、指标体系构建难点1、管理视角2、业务视角3、技术视角 四、指标体系构建原则1、与战略目标对齐2、综合和平衡3、数据可获得性4、可操作性5、具体和可衡量6、参与和…
阅读更多...
lua学习笔记20（lua中一些自带库的学习）

lua学习笔记20（lua中一些自带库的学习）

print("*****************************lua中一些自带库的学习*******************************") print("*************时间***************") --系统时间 print(os.time()) --自己传入参数得到时间 print(os.time({year2011,month4,day5})) --os.data(&qu…
阅读更多...
00 【哈工大_操作系统】Bochs 汇编级调试方法及指令

00 【哈工大_操作系统】Bochs 汇编级调试方法及指令

本文将介绍一下哈工大李治军老师《操作系统》课程在完成Lab时所使用到的 Bochs 调试工具的使用方法。这是一款汇编级调试工具，打开调试模式非常简单，只需在终端下输入如下指令： 1、bochs 调试基本指令大全 功能指令举例在某物理地址设置断点…
阅读更多...
Xxl-job执行器自动注册不上的问题

Xxl-job执行器自动注册不上的问题

今天新建的项目要部署xxl-job，之前部署过好多次，最近没怎么部署，生疏了。部署完之后，服务一直没有注册到执行器管理里面，找了半天也没找到原因，看数据库里的xxl_job_registry表也是一直有数据进来。 后来看…
阅读更多...
小白也能看懂的BEV感知（一）

小白也能看懂的BEV感知（一）

1. 引言 随着人工智能技术的不断发展，自动驾驶越来越多地出现在我们的视野中，智能化和电动化已经成为汽车行业的主旋律。无论是从研究的角度还是从工程的角度来看，它都像是一个巨大的宝藏，等待着我们去探索。本文将介绍这一技术的…
阅读更多...
从51到ARM裸机开发实验(009)LPC2138 中断实验

从51到ARM裸机开发实验(009)LPC2138 中断实验

一、场景设计 中断的概念在《从51到ARM裸机开发实验(007) AT89C51 中断实验》中已经介绍过，LPC2138的Keil工程创建在《从51到ARM裸机开发实验(005)LPC2138 GPIO实验》中已经介绍过。本次使用LPC2138来实现一个这样的场景：四个LED依次亮灭，时间…
阅读更多...
测试人必看，小程序常见问题

测试人必看，小程序常见问题

小程序是一种轻盈的存在，用户无需为了使用它而下载和安装。它依附于微信这个强大的平台，只需轻轻一扫或一搜，它便跃然屏上，随时服务。小程序为我们带来更多前所未有的惊喜和便利，以下分享关于小程序相关的热门问题。 …
阅读更多...
链表基础3——单链表的逆置

链表基础3——单链表的逆置

链表的定义 #include <stdio.h> #include <stdlib.h> typedef struct Node { int data; struct Node* next; } Node; Node* createNode(int data) { Node* newNode (Node*)malloc(sizeof(Node)); if (!newNode) { return NULL; } newNode->data …
阅读更多...
逆向IDA中Dword，数据提取

逆向IDA中Dword，数据提取

我们可以看见数据是这样的&#xff0c;第一个是1cc 但是我们shifte就是 这个因为他的数据太大了&#xff0c;导致高位跑后面去了 这个时候&#xff0c;我们右键——convert——dword 这样就可以提取到争取的数据了 比如第一个数据 0x1cc a0xcc b0x1 print(hex((b<<8…
阅读更多...
HarmonyOS开发实例：【事件的订阅和发布】

HarmonyOS开发实例：【事件的订阅和发布】

介绍 本示例主要展示了公共事件相关的功能&#xff0c;实现了一个检测用户部分行为的应用。具体而言实现了如下几点功能&#xff1a; 1.通过订阅系统公共事件&#xff0c;实现对用户操作行为&#xff08;亮灭屏、锁屏和解锁屏幕、断联网&#xff09;的监测&#xff1b; 2.通…
阅读更多...
vmware安装ubuntu-18.04系统

vmware安装ubuntu-18.04系统

一、软件下载 百度网盘&#xff1a; 链接&#xff1a;https://pan.baidu.com/s/1fK2kygRdSux1Sr1sOKOtJQ 提取码&#xff1a;twsb 二、安装ubuntu系统 1、把ubuntu-18.04的压缩包下载下来&#xff0c;并且解压 2、打开vmware软件&#xff0c;点击文件-打开 3、选择我们刚刚解…
阅读更多...
6. Django 深入模板

6. Django 深入模板

6. 深入模板 6.1 Django模板引擎 Django内置的模板引擎包含模板上下文(亦可称为模板变量), 标签和过滤器, 各个功能说明如下: ● 模板上下文是以变量的形式写入模板文件里面, 变量值由视图函数或视图类传递所得. ● 标签是对模板上下文进行控制输出, 比如模板上下文的判断和循…
阅读更多...
项目7-音乐播放器1+BCrypt加密

项目7-音乐播放器1+BCrypt加密

1.创建项目 1.1 引入依赖 1.2 yml相关配置 application.yml spring:profiles:active: prod mybatis:mapper-locations: classpath:mapper/**Mapper.xmlconfiguration:map-underscore-to-camel-case: true #配置驼峰⾃动转换log-impl: org.apache.ibatis.logging.stdout.StdO…
阅读更多...
openGauss学习笔记-261 openGauss性能调优-使用Plan Hint进行调优-将部分Error降级为Warning的Hint

openGauss学习笔记-261 openGauss性能调优-使用Plan Hint进行调优-将部分Error降级为Warning的Hint

文章目录 openGauss学习笔记-261 openGauss性能调优-使用Plan Hint进行调优-将部分Error降级为Warning的Hint261.1 功能描述261.2 语法格式261.3 示例261.3.1 忽略非空约束261.3.2 忽略唯一约束261.3.3 忽略分区表无法匹配到合法分区261.3.4 更新/插入值向目标列类型转换失败 o…
阅读更多...
【算法】数组元素循环右移k位，并要求只用一个元素大小的附加存储，元素移动或交换次数为O(n)

【算法】数组元素循环右移k位，并要求只用一个元素大小的附加存储，元素移动或交换次数为O(n)

两种写法思路&#xff1a; 思路一&#xff1a;三次倒置 前言&#xff1a;C/C函数 reverse 是 左闭右开区间的&#xff0c;作用是将指定范围数组元素全部倒置&#xff0c;数组从 0 开始&#xff0c;这里主要讲解思路&#xff0c;就直接用 函数 reverse 简化过程 这个方法 实现 …
阅读更多...
vue3第十八节（diff算法）

vue3第十八节（diff算法）

引言&#xff1a; 上一节说了key的用途&#xff0c;而这个key属性&#xff0c;在vue的vnode 中至关重要&#xff0c;直接影响了虚拟DOM的更新机制&#xff1b; 什么场景中会用到diff算法 如&#xff1a;修改响应式属性需要重新渲染页面&#xff0c;会重新执行render渲染函数返…
阅读更多...
为了执行SQL语句，MySQL的架构是怎样设计的

为了执行SQL语句，MySQL的架构是怎样设计的

1. 把MySQL当个黑盒子一样执行SQL语句 上一讲我们已经说到&#xff0c;我们的系统采用数据库连接池的方式去并发访问数据库&#xff0c;然后数据库自己其实也会维护一个连 接池&#xff0c;其中管理了各种系统跟这台数据库服务器建立的所有连接 我们先看下图回顾一下 当我们的…
阅读更多...
数据可视化-ECharts Html项目实战（12）

数据可视化-ECharts Html项目实战（12）

在之前的文章中&#xff0c;我们深入学习ECharts特殊图表中的矩形树图以及Echarts中高级功能的多图表联动。想了解的朋友可以查看这篇文章。同时&#xff0c;希望我的文章能帮助到你&#xff0c;如果觉得我的文章写的不错&#xff0c;请留下你宝贵的点赞&#xff0c;谢谢。 数…
阅读更多...
Directory Monitor：全方位监控文件系统变动的专业利器

Directory Monitor：全方位监控文件系统变动的专业利器

目录 一、软件介绍 二、软件功能 三、软件特点 四、安装说明 五、使用说明 一、软件介绍 Directory Monitor是一款强大易用的实时文件系统监视工具&#xff0c;它由Michael Humpa开发&#xff0c;专为满足用户监控特定目录下文件和子目录变化的需求。无论是为了保障系统安…
阅读更多...
python与设计模式之工厂模式的那些事儿

python与设计模式之工厂模式的那些事儿

一、工厂模式 工厂模式实现了按需创建的最佳模式&#xff0c;其目的是为了隐藏创建类的细节与过程&#xff0c;通过一个统一的接口来创建所需的对象。 话说没了皇位争夺权的皇三接到了一个外征的工作&#xff0c;始皇给了5个亿的经费让皇三组建一个军队。打权总是要进行武器采…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023