1. 线性共轭梯度法

共轭梯度法（英语：Conjugate gradient method），是求解系数矩阵为对称正定矩阵的线性方程组的数值解的方法。

共轭梯度法是一个迭代方法，它适用于

1. 求解线性方程组，

2. 共轭梯度法也可以用于求解无约束的最优化问题。

我们想最小化目标函数f(x)，假设其拥有二次形式：

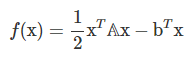
最优化问题表示如下：

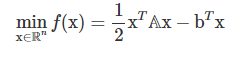
上式可以等价于求解线性方程组 Ax = b，因为

目标方程的梯度为：

此外，双共轭梯度法（英语：BiConjugate gradient method）提供了一种处理非对称矩阵情况的推广。

共轭梯度法中，搜索方向p，是关于A共轭的，即

因此也称为共轭方向（conjugate directions）。

示例：

代码：

import numpy as np# Define the objective function
def f(x): return x[0]**2/2 + x[0]*x[1] + x[1]**2 - 2*x[1]# Define A and b
A = np.array(([1/2, 1/2], [1/2, 1]), dtype=float)
b = np.array([0., 2.])# Make sure A is a symmetric positive definite matrix.
if (A.T==A).all()==True: print("A is symmetric")
eigs = np.linalg.eigvals(A)
print("The eigenvalues of A:", eigs)
if (np.all(eigs>0)):print("A is positive definite")
elif (np.all(eigs>=0)):print("A is positive semi-definite")
else:print("A is negative definite")# Implements the linear conjugate gradient algorithm
def linear_CG(x, A, b, epsilon):res = A.dot(x) - b # Initialize the residualdelta = -res # Initialize the descent directionwhile True:if np.linalg.norm(res) <= epsilon:return x, f(x) # Return the minimizer x* and the function value f(x*)D = A.dot(delta)beta = -(res.dot(delta))/(delta.dot(D)) # Line (11) in the algorithmx = x + beta*delta # Generate the new iterateres = A.dot(x) - b # generate the new residualchi = res.dot(D)/(delta.dot(D)) # Line (14) in the algorithm delta = chi*delta -  res # Generate the new descent direction# Solve the equations
sol, funValue = linear_CG(np.array([2.3, -2.2]), A, b, 1e-5)# Check the result
if ( np.linalg.norm(A@sol - b) < 1e-5):print("solution verified")

2. 非线性共轭梯度法 Nonlinear Conjugate Gradient method

NCG方法被用来解非线性优化问题，常见下面几种算法：

• Fletcher-Reeves algorithm,
• Polak-Ribiere algorithm,
• Hestenes-Stiefel algorithm,
• Dai-Yuan algorithm, and
• Hager-Zhang algorithm.

CG方法第一次被用来解非线性优化问题，是由Fletcher和Reeves提出的。搜索方向delta关于A共轭。

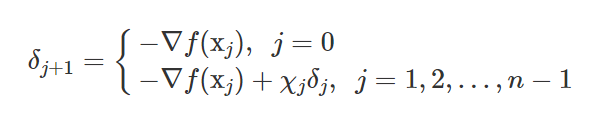
 chi计算式如下：

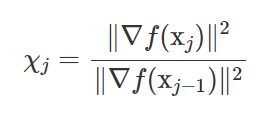
NCG的迭代公式为：

其中delta为方向，beta为步长。

示例：

代码：

首先安装自动微分工具 

pip install autograd

使用了autograd里面的梯度求解函数

此外，用到了 scipy中的line_search函数

scipy.optimize.line_search — SciPy v1.13.0 Manual

import numpy as np
from autograd import grad# Define the objective function
def func(x): # Objective functionreturn x[0]**4 - 2*x[0]**2*x[1] + x[0]**2 + x[1]**2 - 2*x[0] + 1Df = grad(func) # Gradient of the objective function# Next we define the function Fletcher_Reeves()
from scipy.optimize import line_search
NORM = np.linalg.normdef Fletcher_Reeves(Xj, tol, alpha_1, alpha_2):x1 = [Xj[0]]x2 = [Xj[1]]D = Df(Xj)delta = -D # Initialize the descent directionwhile True:start_point = Xj # Start point for step length selection beta = line_search(f=func, myfprime=Df, xk=start_point, pk=delta, c1=alpha_1, c2=alpha_2)[0] # Selecting the step lengthif beta!=None:X = Xj+ beta*delta #Newly updated experimental pointif NORM(Df(X)) < tol:x1 += [X[0], ]x2 += [X[1], ]return X, func(X) # Return the resultselse:Xj = Xd = D # Gradient at the preceding experimental pointD = Df(Xj) # Gradient at the current experimental pointchi = NORM(D)**2/NORM(d)**2 # Line (16) of the Fletcher-Reeves algorithmdelta = -D + chi*delta # Newly updated descent directionx1 += [Xj[0], ]x2 += [Xj[1], ]sol, funValue = Fletcher_Reeves(np.array([2., -1.8]), 10**-5, 10**-4, 0.38)
print(sol)

最后的解为 [1, 1]，f(x)最小值为0

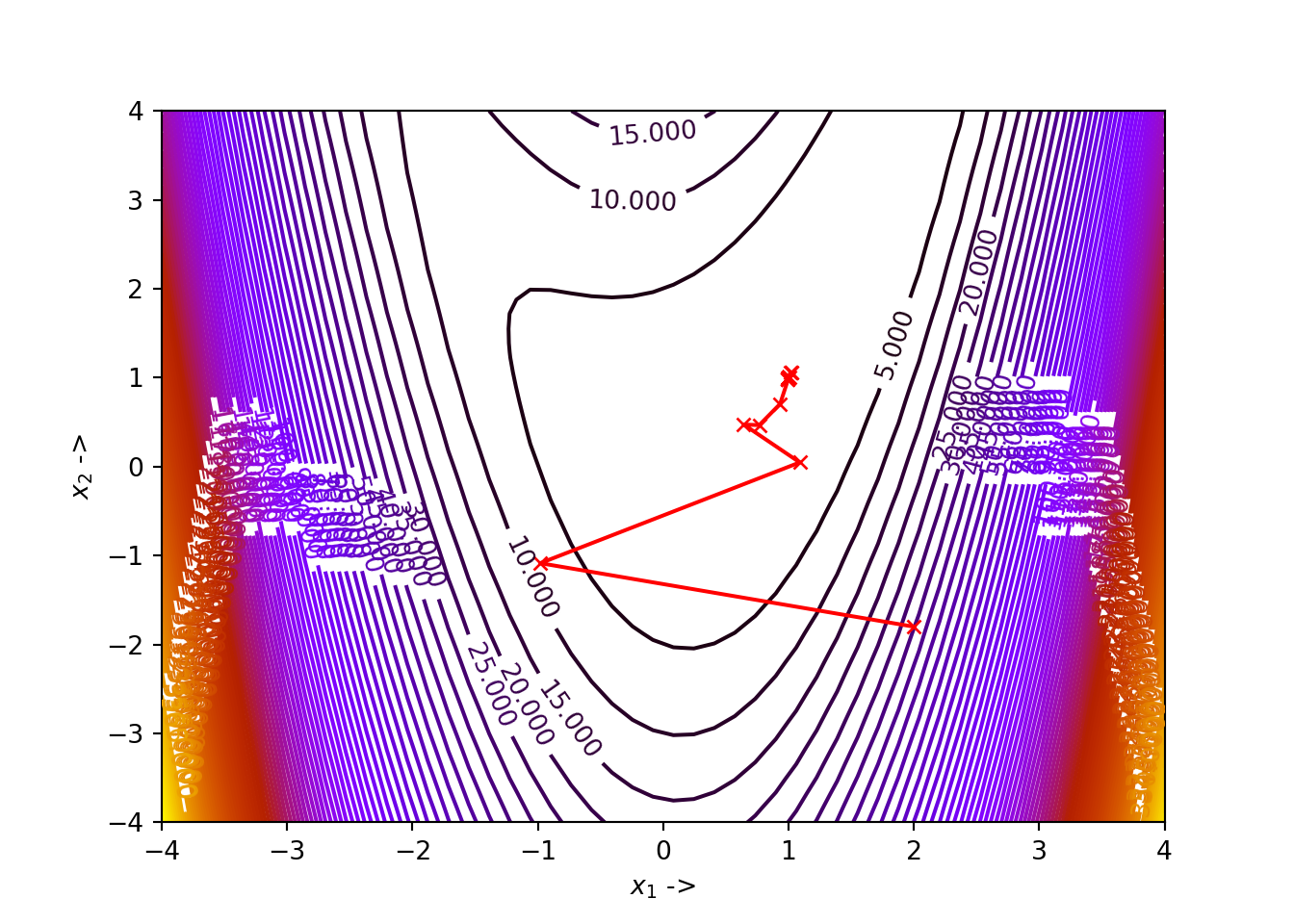
迭代过程如下：

## +----+-----------+------------+--------------+--------------+
## |    |       x_1 |        x_2 |         f(X) |     ||grad|| |
## |----+-----------+------------+--------------+--------------|
## |  0 |  2        | -1.8       | 34.64        | 49.7707      |
## |  1 | -0.98032  | -1.08571   |  8.1108      | 12.6662      |
## |  2 |  1.08966  |  0.0472277 |  1.30794     |  5.6311      |
## |  3 |  0.642619 |  0.473047  |  0.131332    |  0.877485    |
## |  4 |  0.766371 |  0.46651   |  0.0691785   |  0.260336    |
## |  5 |  0.932517 |  0.704482  |  0.0318138   |  0.583346    |
## |  6 |  1.0149   |  1.06008   |  0.00112543  |  0.110081    |
## |  7 |  1.02357  |  1.0596    |  0.000697231 |  0.0238509   |
## |  8 |  1.02489  |  1.05473   |  0.000638128 |  0.0331525   |
## |  9 |  1.00544  |  0.999549  |  0.000158528 |  0.0609372   |
## | 10 |  0.996075 |  0.987011  |  4.19723e-05 |  0.016347    |
## | 11 |  0.994792 |  0.986923  |  3.43476e-05 |  0.00538401  |
## | 12 |  0.994466 |  0.987575  |  3.25511e-05 |  0.00620548  |
## | 13 |  0.9956   |  0.992867  |  2.20695e-05 |  0.015708    |
## | 14 |  0.999909 |  1.00171   |  3.59093e-06 |  0.008628    |
## | 15 |  1.00088  |  1.00254   |  1.3779e-06  |  0.00206337  |
## | 16 |  1.00102  |  1.00249   |  1.24228e-06 |  0.000925229 |
## | 17 |  1.00106  |  1.00226   |  1.14704e-06 |  0.00161353  |
## | 18 |  1.00056  |  1.00065   |  5.3011e-07  |  0.00313135  |
## | 19 |  0.999916 |  0.99956   |  8.14653e-08 |  0.00107299  |
## | 20 |  0.999816 |  0.999511  |  4.85294e-08 |  0.000269684 |
## | 21 |  0.999798 |  0.999526  |  4.57054e-08 |  0.000185146 |
## | 22 |  0.999803 |  0.999615  |  3.90603e-08 |  0.000435884 |
## | 23 |  0.99995  |  0.999991  |  1.08357e-08 |  0.000499645 |
## | 24 |  1.00003  |  1.00009   |  2.25348e-09 |  0.000130632 |
## | 25 |  1.00004  |  1.00009   |  1.75917e-09 |  3.97529e-05 |
## | 26 |  1.00004  |  1.00009   |  1.66947e-09 |  4.22905e-05 |
## | 27 |  1.00003  |  1.00006   |  1.1931e-09  |  0.000108964 |
## | 28 |  1        |  0.999989  |  2.11734e-10 |  6.79786e-05 |
## | 29 |  0.999994 |  0.999982  |  7.24881e-11 |  1.61034e-05 |
## | 30 |  0.999993 |  0.999982  |  6.4458e-11  |  6.72611e-06 |
## +----+-----------+------------+--------------+--------------+

参考链接：

Chapter 5 Conjugate Gradient Methods | Introduction to Mathematical Optimization