目录

P3379：最近公共祖先LCA

思路：

货车运输

---

        

       

P3379：最近公共祖先LCA

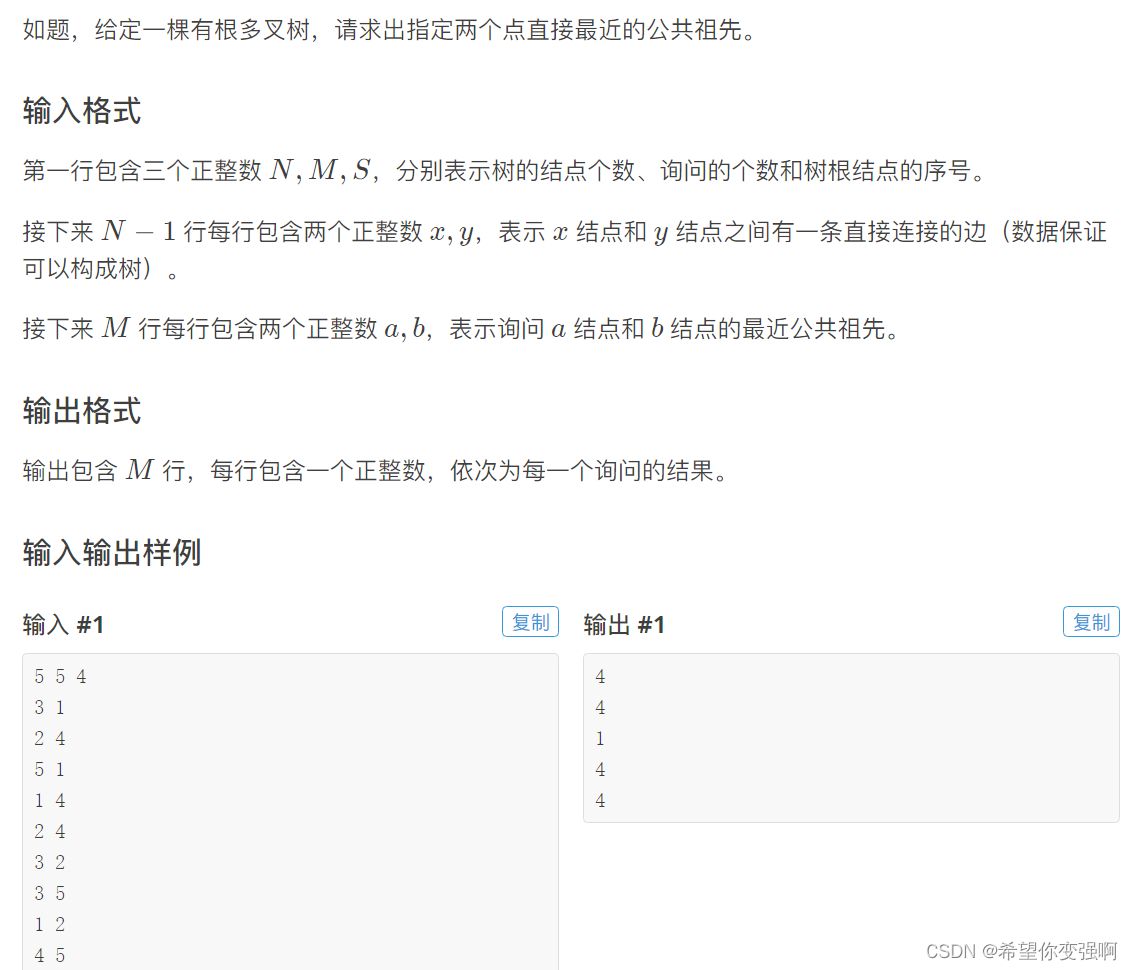
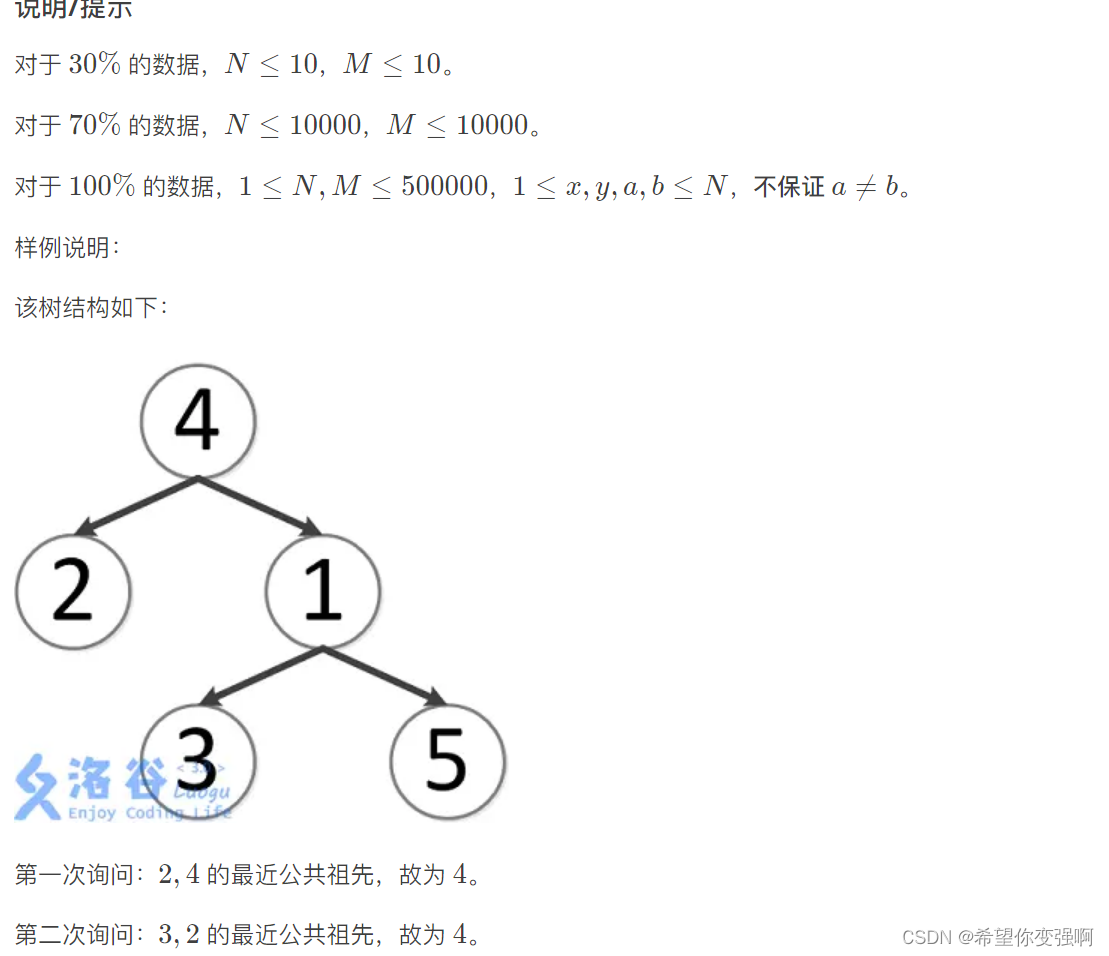
思路：

首先进行的预处理，将所有点的深度和p数组求出来

设置：p[i][j]存的从i向上走2的j次方那么长的路径到的父节点

更深的点走到和另一个点相同的深度(倍增快速逼近)，然后两个点同时走到最下端的公共祖先(倍增快速逼近)

#include<bits/stdc++.h> 
using namespace std;
const int N=500005;
int n,m,s;
vector<int>ve[N];
int d[N],p[N][21];//d存的是深度（deep）,p[i][j]存的从i向上走2的j次方那么长的路径到的父节点     
void dfs(int u,int fa){//首先预处理，将所有点的deep值dfs出来，完成p表的创建for(auto v: ve[u]){if(v==fa)continue;d[v]=d[u]+1;p[v][0]=u;dfs(v,u);}
}                              
int lca(int a,int b){ //非常标准的lca查找（两次逼近）if(d[a]>d[b]) swap(a,b);   //保证a是在b结点上方for(int i=20;i>=0;i--)if(d[a]<=d[p[b][i]]) b=p[b][i]; //达到同一深度if(a==b) return a;  //特判for(int i=20;i>=0;i--)if(p[a][i]!=p[b][i]) a=p[a][i],b=p[b][i];  //向上逼近A和B一起向上return p[a][0];  //最后再向上走一步
}int main(){int a,b;scanf("%d%d%d",&n,&m,&s);//n个结点，m次询问，s是树根编号for(int i=1;i<n;i++){scanf("%d%d",&a,&b);ve[a].push_back(b);ve[b].push_back(a);              }d[s]=1;dfs(s,0);//初始化每个点的deep和p[v][0]for(int j=1;j<=20;j++)for(int i=1;i<=n;i++)p[i][j]=p[p[i][j-1]][j-1];for(int i=1;i<=m;i++){scanf("%d%d",&a,&b);printf("%d\n",lca(a,b));}return 0;
}

        

        

货车运输

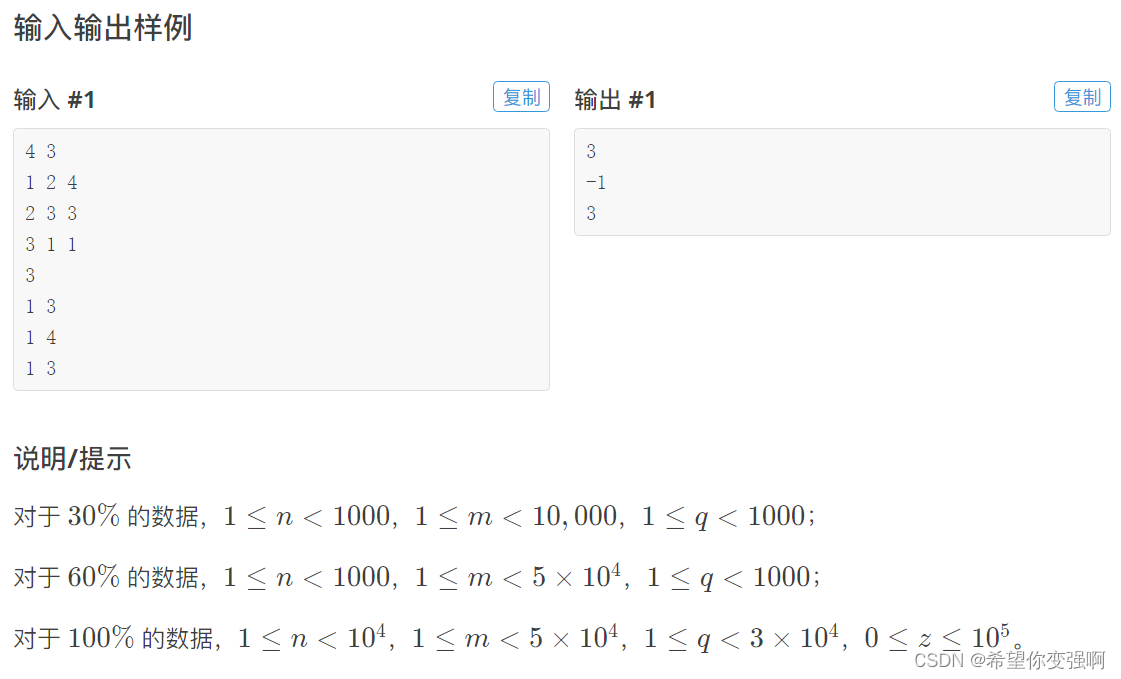
一模一样，就拿这道做过的题来说把：

题意是要路径上最小的权值链路最大，如果是单源问题还是可以dijkstra的。

但是这个题是多源问题，就要kruskal+lca。

首先解释一下为什么要用kruskal：

那么不妨假设求u到v的路径，我们要所有由u通往v的路径中最小边权中最大的路径，那么如果我们按照最大生成树去建图，是不是图中任意两点间建立的路径都是最大路径？因为那些更小的边我们都没用上。可以设想一下如果u到v还有别的额外的路径，那么这些路径之所有没有没用上，不就是因为有的边权太小了。

然后是lca：

我们在建完树后，为什么就会想到lca呢？

首先这个时候我们要求两个点的路径，其实已经变得唯一了，而且必须找到最近公共祖先，所以需要用到lca

其次我们要求u到v的最小边权，那么这个最小边权如果一个一个的跑不就又变成n^n了吗，怎么办？这时候可以想到离线求极值的方法：倍增，线段树。

说到树上倍增，你最快的是不是想到lca

所以我们可以设置w[i][j]表示从i开始向上走2^j到长度对应的小的权值。然后从i开始走2^j长度路径上的最小权值。

同样设置：f[i][j]表示从i开始向上走2^j到的节点

这样就可以在逼近的时候一遍使用w来更新答案，一边使用f找公共祖先

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10,M=3e5+5,inf=1e9;
int tot,n,m,q,head[N],deep[N],f[N][21],w[N][21],fa[N];
//f[i][j]表示从i开始向上走2^j到的节点，w[i][j]表示从i开始向上走2^j到长度对应的小的权值
bool vis[N];
struct edge1{int u,v,w;}e1[M];
struct edge2{int v,w,next;}e2[N];
int find(int x){if(x!=fa[x])fa[x]=find(fa[x]);return fa[x];
}
void add(int u,int v,int w){e2[++tot]=(edge2){v,w,head[u]};head[u]=tot;}
bool cmp(edge1 a,edge1 b){return a.w>b.w;}
void kruskal(){for(int i=1;i<=n;i++) fa[i]=i;//初始化并查集sort(e1+1,e1+1+m,cmp);//建立最大生成树for(int i=1;i<=m;i++){ int u=e1[i].u,v=e1[i].v,w=e1[i].w;int f1=find(u),f2=find(v);if(f1!=f2){ //建立重构树fa[f1]=f2;//合并并查集add(u,v,w);add(v,u,w);}}
}
void dfs(int u,int faa){//初始化每个点的deep[v]，f[v][0]，w[v][0]vis[u]=1;for(int i=head[u];i;i=e2[i].next){int v=e2[i].v;if(v==faa)continue;deep[v]=deep[u]+1;f[v][0]=u;w[v][0]=e2[i].w;dfs(v,u);//先更新自己再更新孩子}
}
int lca(int x,int y){if(find(x)!=find(y))return -1;int ans=inf;if(deep[x]>deep[y])swap(x,y);//让左边y向右边x靠近for(int i=20;i>=0;i--){//达到相同深度if(deep[f[y][i]]>=deep[x]){ans=min(ans,w[y][i]); y=f[y][i];//每上升一次就要更新此距离上的最小值。修改y位置}}if(x==y)return ans;//第一次返回for(int i=20;i>=0;i--){//一起上升到没有公共祖先为止if(f[x][i]!=f[y][i]){ans=min(ans,min(w[x][i],w[y][i]));//每上升一次就要更新两段距离上的最小值。x=f[x][i];y=f[y][i];}}ans=min(ans,min(w[x][0],w[y][0]));//此时再往上一格就是lca，所以再更新一次return ans;
}
int main(){cin>>n>>m>>q;for(int i=1;i<=m;i++){cin>>e1[i].u>>e1[i].v>>e1[i].w;}kruskal();for(int i=1;i<=n;i++){if(vis[i])continue;deep[i]=1;dfs(i,0);f[i][0]=i;w[i][0]=inf;//初始化根的信息}for(int i=1;i<=20;i++){//初始化倍增表for(int j=1;j<=n;j++){f[j][i]=f[f[j][i-1]][i-1];//距离倍增表w[j][i]=min(w[j][i-1],w[f[j][i-1]][i-1]);//极值倍增表}}int x,y;for(int i=1;i<=q;i++){cin>>x>>y;cout<<lca(x,y)<<'\n';}return 0;}

当然如果你只是骗分，那么直接floyd就可以。

设置dp[i][j]表示i到j路径上的存在的最小边权，

根据： dp[i][j]=max(dp[i][j],min(dp[i][k],dp[k][j]))进行转移

当然前提是i能到k，k能到j 。然后至少能拿小半分了。

 memset(dp,-1,sizeof(dp));cin>>n>>m>>q;while(m--){int u,v,x;cin>>u>>v>>x;dp[u][v]=max(dp[u][v],x);   //如果有重边，选稳定性最大的一条路dp[v][u]=max(dp[v][u],x);}for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i!=j&&j!=k&&i!=k){   //用K中转的路径 更新dp[i][j]dp[i][j]=max(dp[i][j],min(dp[i][k],dp[k][j]));}}}}while(q--){int x,y;cin>>x>>y;cout<<dp[x][y]<<endl;}