第八章 贪心算法 part05

1.LeetCode. 无重叠区间

1.1题目链接：435. 无重叠区间

文章讲解：代码随想录
视频讲解：B站卡哥视频

1.2思路：我来按照右边界排序，从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。

此时问题就是要求非交叉区间的最大个数。

这里记录非交叉区间的个数还是有技巧的，如图：

区间，1，2，3，4，5，6都按照右边界排好序。

当确定区间 1 和 区间2 重叠后，如何确定是否与 区间3 也重贴呢？

就是取 区间1 和 区间2 右边界的最小值，因为这个最小值之前的部分一定是 区间1 和区间2 的重合部分，如果这个最小值也触达到区间3，那么说明 区间 1，2，3都是重合的。

接下来就是找大于区间1结束位置的区间，是从区间4开始。那有同学问了为什么不从区间5开始？别忘了已经是按照右边界排序的了。

区间4结束之后，再找到区间6，所以一共记录非交叉区间的个数是三个。

总共区间个数为6，减去非交叉区间的个数3。移除区间的最小数量就是3。

1.3附加代码如下所示：

//该题目和之前的射箭气球问题很相似
class Solution {
public:static bool cmp(const vector<int>&a,const vector<int>&b){return a[0]<b[0];}int eraseOverlapIntervals(vector<vector<int>>& intervals) {if(intervals.size()==0)return 0;int result=0;sort(intervals.begin(),intervals.end(),cmp);for(int i=1;i<intervals.size();i++)//如果当前区间左边界大于前一个区间的有边界就不需要进行移除区间操作{if(intervals[i][0]>=intervals[i-1][1]){continue;}else//当前{intervals[i][1]=min(intervals[i][1],intervals[i-1][1]);result++;}}return result;}
};

2.LeetCode.划分字母区间

2.1题目链接：763.划分字母区间

文章讲解：代码随想录
视频讲解：B站卡哥视频

2.2思路：在遍历的过程中相当于是要找每一个字母的边界，如果找到之前遍历过的所有字母的最远边界，说明这个边界就是分割点了。此时前面出现过所有字母，最远也就到这个边界了。

可以分为如下两步：

统计每一个字符最后出现的位置
从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点如图：

2.3附加代码如下所示：

class Solution {
public:vector<int> partitionLabels(string s) {vector<int>reuslt;int hash[27]={0};for(int i=0;i<s.size();i++){hash[s[i]-'a']=i;//统计字母最远距离的下标}int left=0;//字符分割的左边界int right=0;//字符分割的右边界for(int i=left;i<s.size();i++){right=max(right,hash[s[i]-'a']);if(right==i)//找到字母最远距离的下标与实际位置对应上了就分割{reuslt.push_back(right-left+1);left=right+1;//更新下一次进行分割的起始点}}return reuslt;}
};

3.LeetCode.合并区间

3.1题目链接：[56. 合并区间(https://leetcode.cn/problems/merge-intervals/)

文章讲解：代码随想录
视频讲解：B站卡哥视频

3.2思路：大家如果认真做题的话，话发现和我们刚刚讲过的452. 用最少数量的箭引爆气球 )和 435. 无重叠区间都是一个套路。

这几道题都是判断区间重叠，区别就是判断区间重叠后的逻辑，本题是判断区间重贴后要进行区间合并。

所以一样的套路，先排序，让所有的相邻区间尽可能的重叠在一起，按左边界，或者右边界排序都可以，处理逻辑稍有不同。

按照左边界从小到大排序之后，如果 intervals[i][0] <= intervals[i - 1][1] 即intervals[i]的左边界 <= intervals[i - 1]的右边界，则一定有重叠。（本题相邻区间也算重贴，所以是<=）

这么说有点抽象，看图：（注意图中区间都是按照左边界排序之后了）

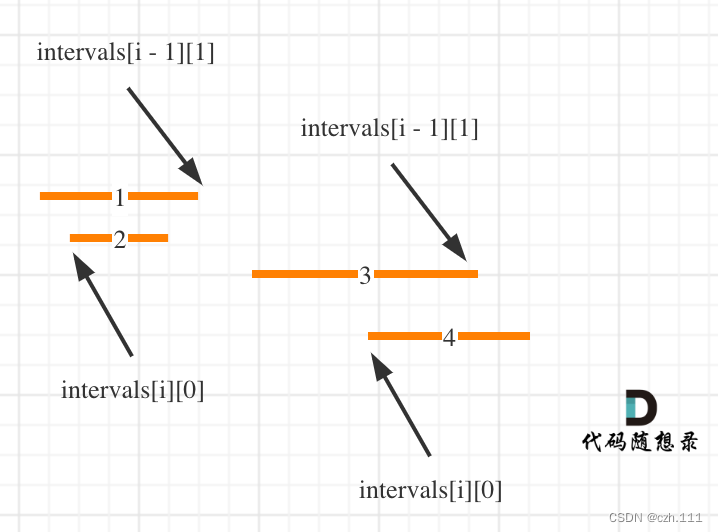
知道如何判断重复之后，剩下的就是合并了，如何去模拟合并区间呢？

其实就是用合并区间后左边界和右边界，作为一个新的区间，加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。

3.3附加代码如下所示：

//精简版
class Solution {
public:static bool cmp(const vector<int>&a,const vector<int>&b){return a[0]<b[0];}vector<vector<int>> merge(vector<vector<int>>& intervals) {vector<vector<int>>result;if(intervals.size()==0)return result;sort(intervals.begin(),intervals.end(),cmp);//按照左边界大小进行排序result.push_back(intervals[0]);//先加入第一个集合区间for(int i=1;i<intervals.size();i++){if(intervals[i][0]>result.back()[1])//前后两个集合没有重叠时候,要和加入result中的进行比较而不是原数组中的{result.push_back(intervals[i]);}else //前后两个集合有重叠时候且后一个右边界大于前一个右边界{result.back()[1]=max(result.back()[1],intervals[i][1]);//左边界是不变的，选择前后两个右边界大的那一个}}return result;}
};