目录

面试题 105 : 最大的岛屿

面试题 106 : 二分图

---

 

---

面试题 105 : 最大的岛屿

题目：

海洋岛屿地图可以用由 0、1 组成的二维数组表示，水平或竖直方向相连的一组 1 表示一个岛屿，请计算最大的岛屿的面积（即岛屿中 1 的数目）。例如，在下图中有 4 个岛屿，其中最大的岛屿的面积为 5。

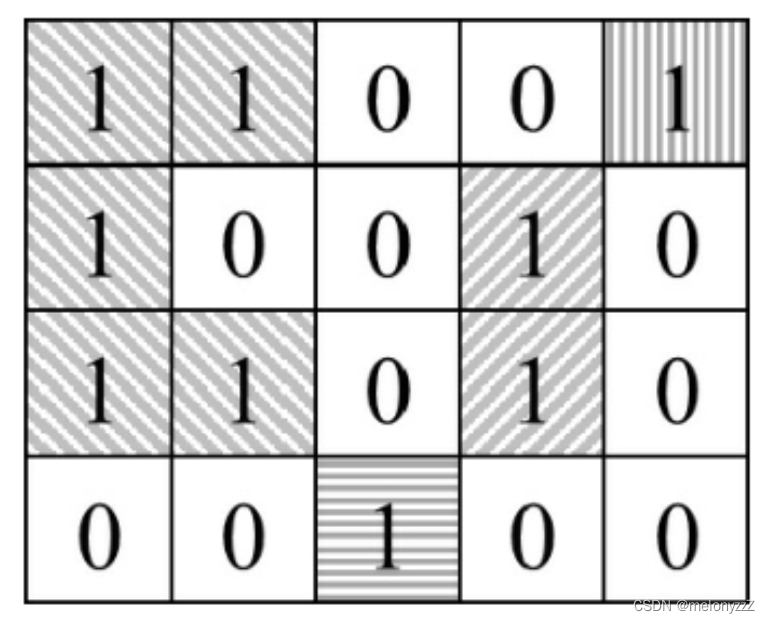
分析：

应用与图相关的算法解决问题的第 1 步是找出问题中隐含的图。看到这个题目之后，可能会有人问：输入的是一个矩阵，图在哪里？其实图是节点（即顶点）和边的集合，因此需要找出图的节点和边。这个题目关注的是地图中的岛屿，也就是矩阵中的 1。矩阵中的每个值为 1 的格子都是图中的一个节点。矩阵中的一个格子可能与位于它上、下、左、右的 4 个格子相邻，两个相邻的值为 1 的格子之间有一条边相连。例如，可以用下图表示上图中的岛屿。

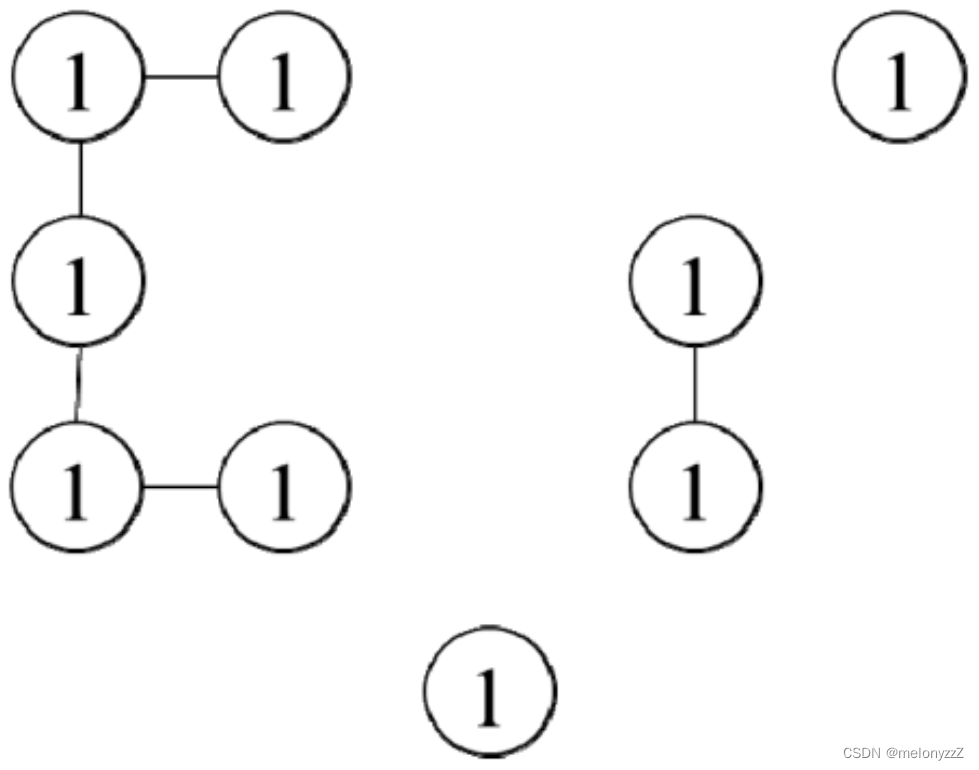
即一个非连通图中有 4 个连通分量，通过计算每个连通分量中节点的数目，就能知道最大的岛屿的面积为 5。

int maxAreaOfIsland(vector<vector<int>>& grid) {int rows = grid.size(), cols = grid[0].size();vector<vector<bool>> isVisited(rows, vector<bool>(cols, false));
​int maxArea = 0;for (int i = 0; i < rows; ++i){for (int j = 0; j < cols; ++j){if (grid[i][j] == 1 && !isVisited[i][j]){int area = getArea(grid, isVisited, i, j);maxArea = max(maxArea, area);}}}return maxArea;
}

广度优先搜索：

int getArea(vector<vector<int>>& grid, vector<vector<bool>>& isVisited, int i, int j) {queue<vector<int>> q;q.push(vector<int>{ i, j });isVisited[i][j] = true;
​vector<vector<int>> dirs = { { -1, 0 }, { 1, 0 }, { 0, -1 }, { 0, 1 } };int area = 0;while (!q.empty()){vector<int> front = q.front();q.pop();++area;
​for (vector<int>& dir : dirs){int r = front[0] + dir[0];int c = front[1] + dir[1];if (r >= 0 && r < grid.size() &&c >= 0 && c < grid[0].size() &&grid[r][c] == 1 && !isVisited[r][c]){q.push(vector<int>{ r, c });isVisited[r][c] = true;}}}return area;
}

上述代码中队列的元素为矩阵中的坐标，每个坐标都包含行号和列号这两个值，用一个长度为 2 的数组表示。

二维数组 dirs 表示在矩阵中向上、下、左、右这 4 个方向前进一步时坐标的变化。在矩阵中向上移动一步时行号减 1 而列号不变，所以坐标的改变值为 (-1, 0)，其他方向的改变值类似。用当前坐标加上坐标的改变值就得到向不同方向前进一步之后的坐标。这样写代码的好处是容易用一个简洁的循环实现向 4 个不同方向前进。

深度优先搜索：

int getArea(vector<vector<int>>& grid, vector<vector<bool>>& isVisited, int i, int j) {isVisited[i][j] = true;int area = 1;
​vector<vector<int>> dirs = { { -1, 0 }, { 1, 0 }, { 0, -1 }, { 0, 1 }};for (vector<int>& dir : dirs){int r = i + dir[0];int c = j + dir[1];if (r >= 0 && r < grid.size() && c >= 0 && c < grid[0].size() &&grid[r][c] == 1 && !isVisited[r][c]){area += getArea(grid, isVisited, r, c);}}return area;
}

---

面试题 106 : 二分图

题目：

如果能将一个图中的节点分成 A、B 两部分，使任意一条边的一个节点属于 A 而另一个节点属于 B，那么该图就是一个二分图。输入一个由数组 graph 表示的图，graph[i] 中包含所有和节点 i 相邻的节点，请判断该图是否为二分图。

例如，如果输入 graph 为 [[1, 3], [0, 2], [1, 3], [0, 2]]，那么可以将节点分为 { 0, 2 }、{ 1, 3 } 两个部分，因此该图是一个二分图，如下图 (a) 所示。如果输入 graph 为 [[1, 2, 3], [0, 2], [0, 1, 3], [0, 2]]，那么该图是一个非二分图，如下图 (b) 所示。

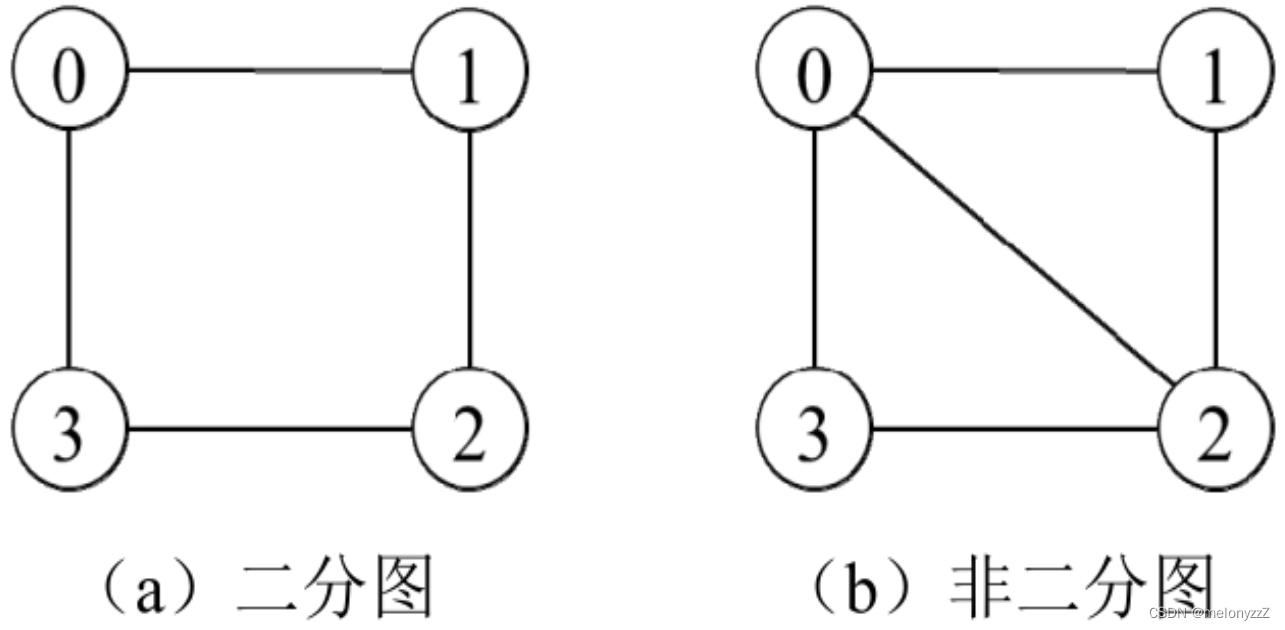
分析：

根据题目提供的信息，二分图的节点可以分成两种不同的类型，任意一条边的两个节点分别属于两种不同的类型。可以为图中的所有节点着色，两种不同类型的节点分别涂上不同的颜色。如果任意一条边的两个节点都能被涂上不同的颜色，那么整个图就是一个二分图。

一个图可能包含多个连通分量，需要逐一对每个连通分量着色。

bool isBipartite(vector<vector<int>>& graph) {int n = graph.size();vector<int> colors(n, -1);for (int i = 0; i < n; ++i){if (colors[i] == -1){if (!setColor(graph, colors, i, 0))return false;}}return true;
}

图中有 n 个节点，于是创建一个长度为 n 的数组 colors 记录每个节点的颜色，节点 i 的颜色保存在 colors[i] 中。

1. 如果节点 i 还没有被着色，那么 colors[i] 的值为 -1；

2. 如果节点 i 已经被着色，那么 colors[i] 的值为 0 或 1。

函数 setColor 用来对以节点 i 为起始节点的一个连通分量着色，它的返回值用来表示能否按照二分图的规则对连通分量的所有节点进行着色。为了能够给所有节点着色，需要搜索所有与节点 i 连通的节点，每搜索到一个尚未着色的节点就按照二分图的规则给它涂上颜色。

利用广度优先搜索对连通分量着色：

bool setColor(vector<vector<int>>& graph, vector<int>& colors, int i, int color) {queue<int> q;q.push(i);colors[i] = color;while (!q.empty()){int pos = q.front();q.pop();for (int adjPos : graph[pos]){if (colors[adjPos] == -1){q.push(adjPos);colors[adjPos] = 1 - colors[pos];}else{if (colors[adjPos] == colors[pos])return false;}}}return true;
}

利用深度优先搜索对连通分量着色：

bool setColor(vector<vector<int>>& graph, vector<int>& colors, int i, int color) {if (colors[i] >= 0)return colors[i] == color;
​colors[i] = color;for (int adjPos : graph[i]){if (!setColor(graph, colors, adjPos, 1 - color))return false;}return true;
}