
目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.结果展示
- 4.参考文献
1.背景
2023年,Jia等人受到自然界小龙虾社会行为启发,提出了小龙虾优化算法(Crayfsh Optimization Algorithm, COA)。
2.算法原理
2.1算法思想
COA基于小龙虾社会行为,主要包括觅食行为、避暑行为和竞争行为。觅食行为和竞争行为是COA的开发阶段,避暑行为是COA的探索阶段。(PS:真香🤣
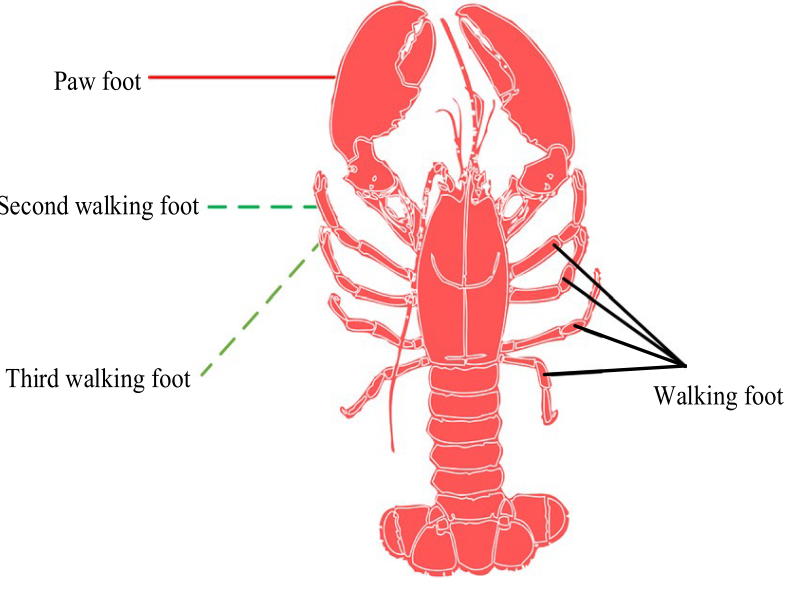
2.2算法过程
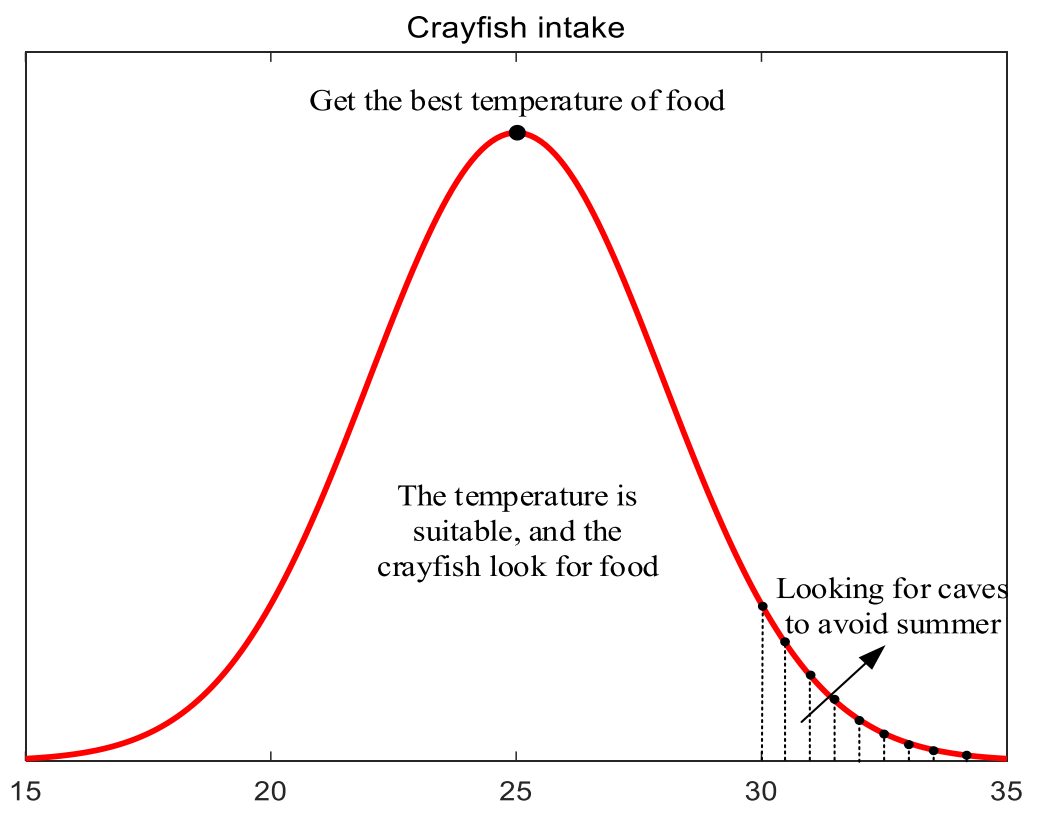
温度和摄入量
温度变化会直接影响小龙虾的行为,当温度超过30摄氏度时,它们更喜欢寻找凉爽的地方。在适宜的温度下(15摄氏度到30摄氏度),小龙虾会增加觅食活动,而最佳温度是25摄氏度。因此,小龙虾的摄取量可近似为正态分布:
p = C 1 × ( 1 2 × π × σ ) × exp ( − ( t e m p − μ ) 2 2 σ 2 ) ) (1) p=C_1\times\left(\frac1{\sqrt{2\times\pi}\times\sigma)}\times\exp\left(-\frac{(temp-\mu)^2}{2\sigma^2}\right)\right)\tag{1} p=C1×(2×π×σ)1×exp(−2σ2(temp−μ)2))(1)
其中,temp为小龙虾当前温度:
t e m p = r a n d × 15 + 20 (2) temp=rand\times15+20\tag{2} temp=rand×15+20(2)
避暑行为(探索阶段)
当温度>30时,温度过高,此时小龙虾就会选择加入洞穴过暑假:
X s h a d e = ( X G + X L ) / 2 (3) X_{shade}=(X_G+X_L)/2\tag{3} Xshade=(XG+XL)/2(3)

其中,XG表示迭个体最优位置,XL表示当前种群的最优位置。
当rand < 0.5时,表示没有其他小龙虾竞争洞穴,小龙虾将直接进入洞穴避暑:
X i , j t + 1 = X i , j t + C 2 × r a n d × ( X s h a d e − X i , j t ) (4) X_{i,j}^{t+1}=X_{i,j}^t+C_2\times rand\times\left(X_{shade}-X_{i,j}^t\right)\tag{4} Xi,jt+1=Xi,jt+C2×rand×(Xshade−Xi,jt)(4)
PS:综合式(3)来看,还是魔改PSO更新方式🤣
C2为递减递减因子,平衡探索与开发:
C 2 = 2 − ( t / T ) (5) C_{2}=2 - (t/T)\tag{5} C2=2−(t/T)(5)
在避暑阶段,小龙虾的目标是靠近洞穴,这代表了最优解。它们会朝着洞穴靠近,使得个体更接近最优解,增强了COA的开发能力,从而使算法收敛更快。
竞争行为(开发阶段)
温度> 30,rand≥0.5时,表明其他小龙虾也对洞穴感兴趣:
X i , j t + 1 = X i , j t − X z , j t + X s h a d e (6) X_{i,j}^{t+1}=X_{i,j}^t-X_{z,j}^t+X_{shade}\tag{6} Xi,jt+1=Xi,jt−Xz,jt+Xshade(6)
z为小龙虾随机个体:
z = r o u n d ( r a n d × ( N − 1 ) ) + 1 (7) z=round(rand\times(N-1))+1\tag{7} z=round(rand×(N−1))+1(7)
在竞争阶段,小龙虾相互竞争,小龙虾Xi根据另一只小龙虾的位置Xz调整自己的位置,扩大了COA的搜索范围,增强了算法的探索能力。
觅食行为(开发阶段)
温度≤30℃时,适合小龙虾摄食:
X f o o d = X G (8) X_{food}=X_G\tag{8} Xfood=XG(8)
其中,Q表述为:
Q = C 3 × r a n d × ( f i t n e s s i / f i t n e s s f o o d ) (9) Q=C_3\times rand\times(fitness_i/fitness_{food})\tag{9} Q=C3×rand×(fitnessi/fitnessfood)(9)
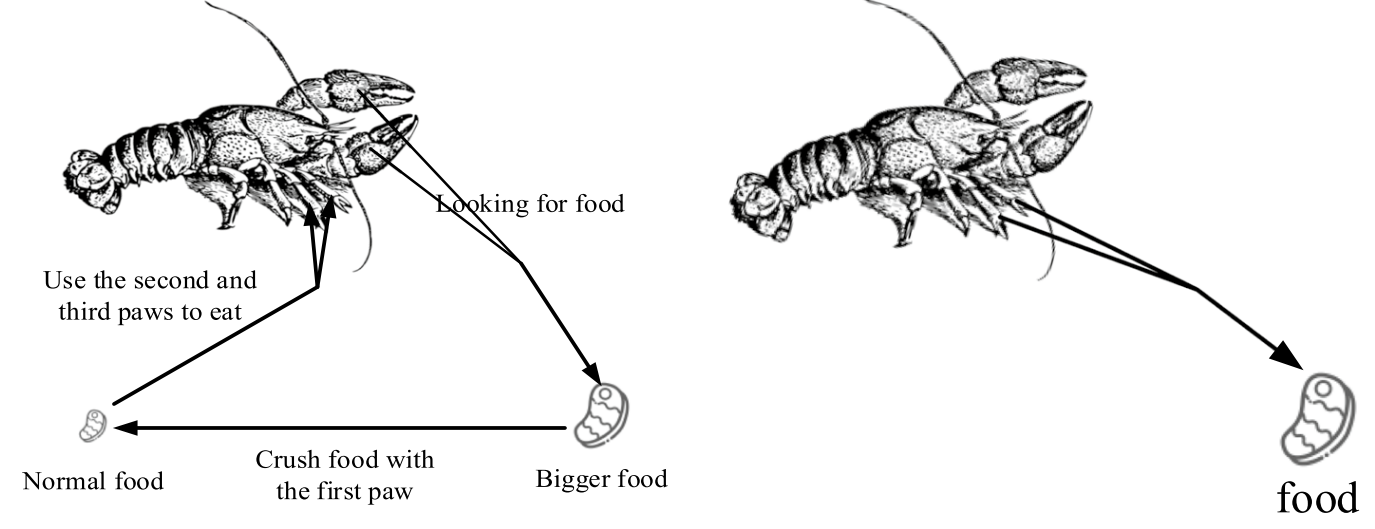
小龙虾对食物大小的判断来自于最大食物的大小。当Q > (C3+1)/ 2时,表示食物太大:
X f o o d = exp ( − 1 Q ) × X f o o d (10) X_{food}=\exp\left(-\frac1Q\right)\times X_{food}\tag{10} Xfood=exp(−Q1)×Xfood(10)
当食物被撕碎变小后,第二和第三只爪子会交替地捡起食物放进嘴里。这里采用正弦函数和余弦函数的组合来模拟交替过程:
X i , j t + 1 = X i , j t + X f o o d × p × ( cos ( 2 × π × r a n d ) − sin ( 2 × π × r a n d ) ) (11) X_{i,j}^{t+1}=X_{i,j}^t+X_{food}\times p\times(\cos{(2\times\pi\times rand)}-\sin{(2\times\pi\times rand)})\tag{11} Xi,jt+1=Xi,jt+Xfood×p×(cos(2×π×rand)−sin(2×π×rand))(11)
当Q≤(C3 +1)/ 2时,小龙虾直接进食:
X i , j t + 1 = ( X i , j t − X f o o d ) × p + p × r a n d × X i , j t (12) X_{i,j}^{t+1}=\left(X_{i,j}^t-X_{food}\right)\times p+p\times rand\times X_{i,j}^t\tag{12} Xi,jt+1=(Xi,jt−Xfood)×p+p×rand×Xi,jt(12)
伪代码

3.结果展示
使用测试框架,测试COA性能 一键run.m
- 【智能算法】省时方便,智能算法统计指标——一键运行~
CEC2005-F8:
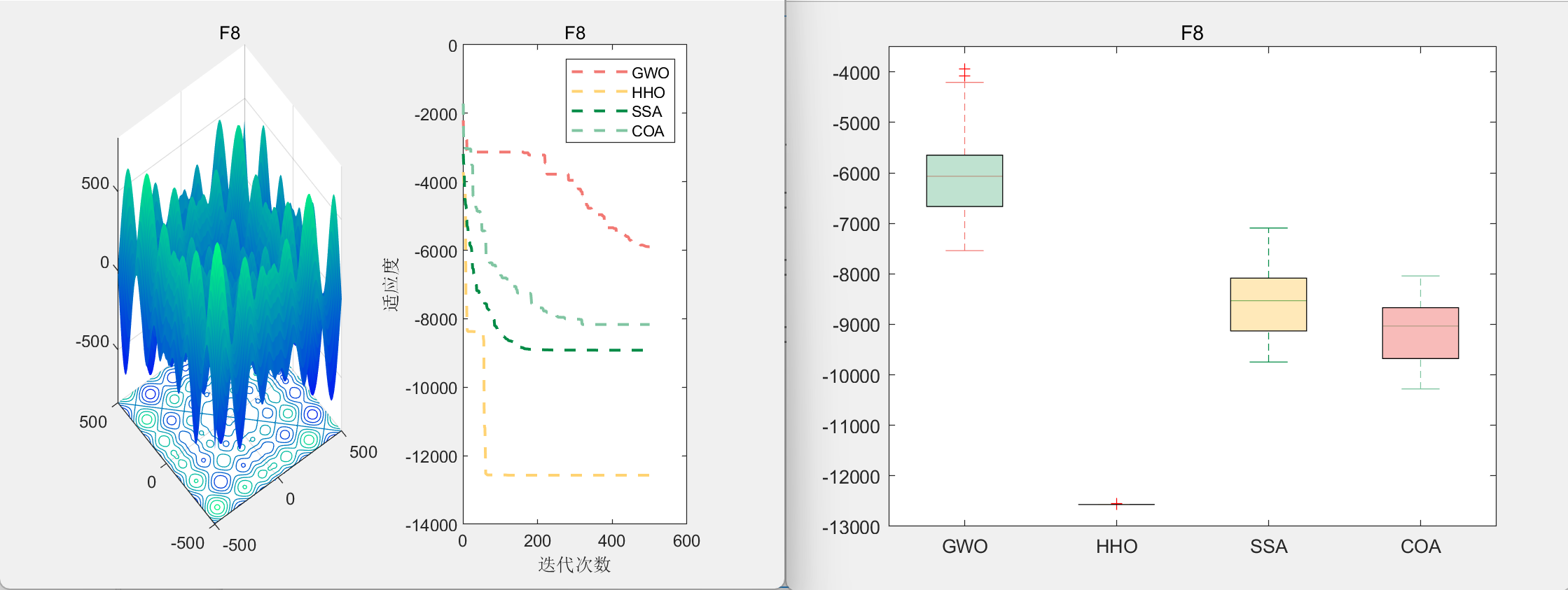
Friedamn检验排名:
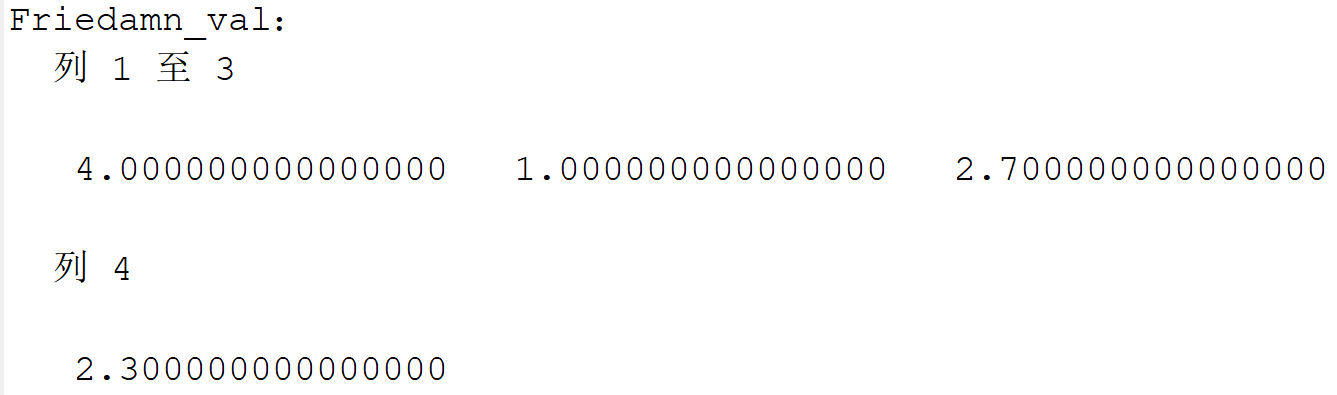
CEC2005-F14:
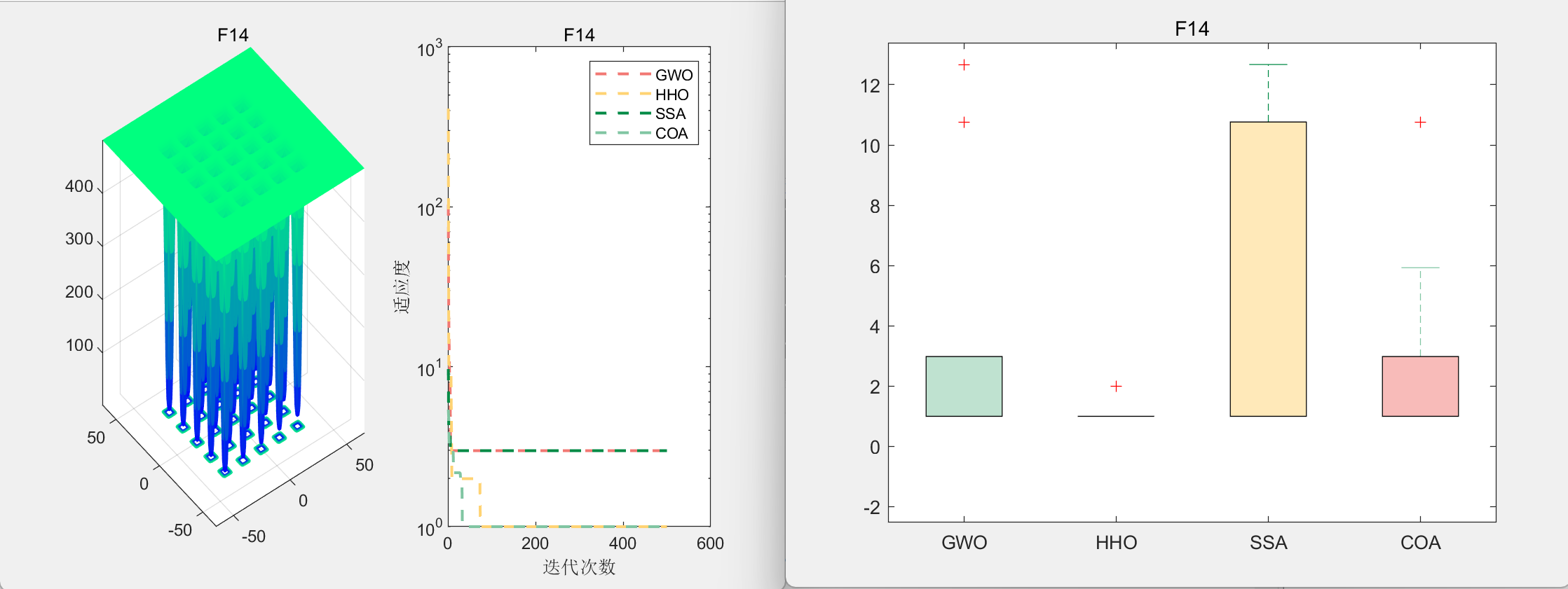
Friedamn检验排名:

PS:COA中规中矩🤣
4.参考文献
[1] Jia H, Rao H, Wen C, et al. Crayfish optimization algorithm[J]. Artificial Intelligence Review, 2023, 56(Suppl 2): 1919-1979.














)

:MySQL中的锁)


