宫侑的发球最终进化为三刀流，那么我的题解也未必要循规蹈矩!

---

1、验证回文串

题目描述：

解法：

        这题官方给的关于双指针的题解都用到了多个库函数，如 tolower(大写字母转小写)、isalnum(判断一个字符是否是 字母 或者 十进制数字 )

        我想避免使用库函数，所有就不用双指针的做法了，而是使用栈！

        思路很简单：

                1、先将字符串中所有字母统一为小写字母

                2、将数字和小写字母入栈，同时将完整的、连续的字符都加入到一个新字符串newS中

                3、再使用一个新字符串stkPop接收栈每一次pop出的字符

                4、比较 newS 和 stkPop 是否相等

        这道题的描述中提到了“字母和数字都属于字母数字字符”，但示例中没有给出串中包含数字的情况，导致测试用例 '0P' 没有通过，这也是因为我忽略了串中还有数字的情况

        要点：

                1、对于大写字母，在 ASCII 码的基础上 +32 就能转为小写字母

                2、栈从top位置开始pop，每次pop后栈中的元素会被删除

class Solution {
public:bool isPalindrome(string s) {stack <char> stk;string newS;string stkPop;  // 接收栈中所有字符pop后的结果if(s.size() <= 1) return true;for(int i = 0; i < s.size(); ++i){if(s[i] >= 'A' && s[i] <= 'Z'){s[i] += 32;  // 先将串中所有大写字母转为小写}// 只将串中的字母和数字入栈if((s[i] >= 'a' && s[i] <= 'z') || (s[i] >= '0' && s[i] <= '9')){stk.push(s[i]); newS += s[i];}}while(!stk.empty()){stkPop += stk.top();stk.pop();}return stkPop == newS;}
};

2、判断子序列

题目描述：

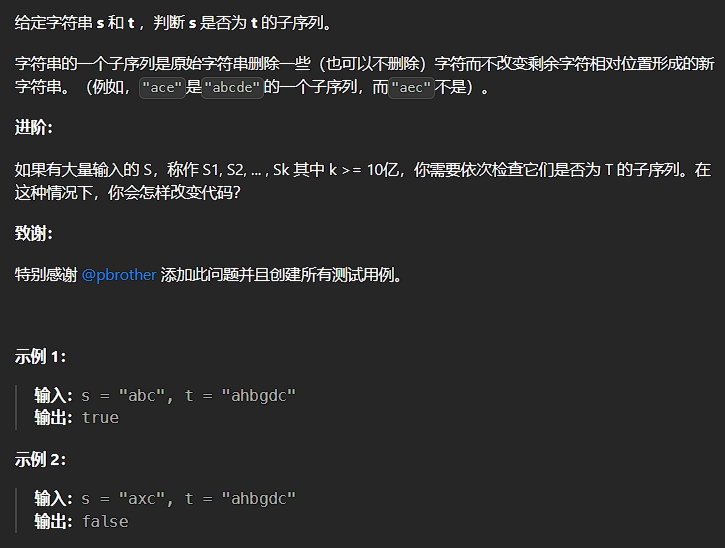
解法：

        看到这种题，第一反应就是2个 for 循环，这种想法很不好

    思路：       

        为串 s 的首字符设置一个指针，同理为串 t 的首字符也设置一个指针

        我们是要在 t 中找出和 s 可以匹配上的子串，当两个串中匹配上了同一个字符时，两个指针都向后走一步，以便进行下一个字符的匹配

        若 s 的第2个字符与 t 的第2个字符没有匹配上，此时指向 s 的指针不动，指向 t 的指针继续向后移动，直到找到匹配项

        当 s 的指针走完整个 s 串时，表示在 t 中有可以匹配上的子序列，而 s 的指针没有走完 s 串时，则没有匹配成功

class Solution {
public:bool isSubsequence(string s, string t) {// 指向字符串s、t首字符的指针int i = 0, j = 0;if(s.size() == 0) return true;for(i, j; j < t.size(); ++j){if(s[i] == t[j]){i++;  // 匹配上了, i 和 j同走，没匹配上,只有 j 往后走if(i == s.size()) return true;}}return false;}
};

3、两数之和Ⅱ-输入有序数组

题目描述：

解法：

        被题目描述中的“给你一个下标从1开始的整数数组”迷惑了，一开始设定的指针是

int i = 1;

int j = numbers.size();

        哈哈哈哈果然溢出了，不论何种描述，数组容器的下标在计算机世界里永远是从0开始的

        最终根据题目要求返回 {i + 1, j + 1} 就好了

        之前只知道python中单个函数可以返回多个值，还在想C++怎么返回两个下标值呢？刚开始甚至还定义了另一个 vector<int> res 来接收下标，最终看了题解后发现了 return  {i + 1, j + 1} 这种写法

class Solution {
public:vector<int> twoSum(vector<int>& numbers, int target) {int i = 0;  // 首指针int j = numbers.size() - 1;  // 尾指针for(i, j; i < numbers.size(), j >= 0;){if((numbers[i] + numbers[j]) > target){j--;  // 两数之和大于目标，尾指针向前走}else if((numbers[i] + numbers[j]) < target){i++;}else{if((numbers[i] + numbers[j]) == target) return {i + 1, j + 1};}}return {-1, -1};}
};

4、盛水最多的容器

题目描述：

        官方写的垂线、端点之类的术语属实费脑子，推荐大家去看K神的题解——(传送门)

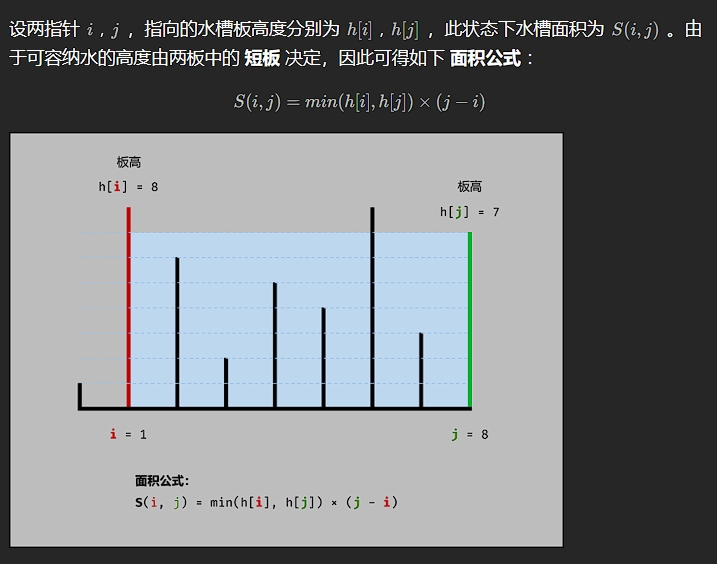
解法：

        实际上求解的正是矩形面积，规定好  i < j 后，唯一要做的就是判断 i 和 j 代表的槽板哪个高哪个低，因为较小的一方才能盛水而不漏

        每次移动槽板较低的一方(此处可能用到了贪心的思想)，通过不断比较原来面积和新面积的大小来返回最终的最大面积。

class Solution {
public:int maxArea(vector<int>& height) {int res = 0;int i = 0;int j = height.size() - 1;while(i < j){// 指针指向的水槽板高度分别为 h[i], h[j],两者中小的一方决定容纳面积res = max(res, (min(height[i], height[j]) * (j - i)));if(height[i] < height[j]) i++;else j--;}return res;}
};