一、什么情况可以使用动态规划

动态规划 = 最优子结构 + 重叠子问题 + 转移方程

最优子结构：保证能从局部解推出全局解，也就是保证能够写出转移方程

重叠子问题：说明暴力解法太耗时，我们可以使用动态规划进行优化

转移方程：动态规划的核心，各种状态必须能够找到一个共同的状态转移方程

「最优子结构」是某些问题的一种特定性质，并不是动态规划问题专有的。也就是说，很多问题其实都具有最优子结构，只是其中大部分不具有重叠子问题，所以我们不把它们归为动态规划系列问题而已。

我先举个很容易理解的例子：假设你们学校有 10 个班，你已经计算出了每个班的最高考试成绩。那么现在我要求你计算全校最高的成绩，你会不会算？当然会，而且你不用重新遍历全校学生的分数进行比较，而是只要在这 10 个最高成绩中取最大的就是全校的最高成绩。

我给你提出的这个问题就符合最优子结构：可以从子问题的最优结果推出更大规模问题的最优结果。让你算每个班的最优成绩就是子问题，你知道所有子问题的答案后，就可以借此推出全校学生的最优成绩这个规模更大的问题的答案。

你看，这么简单的问题都有最优子结构性质，只是因为显然没有重叠子问题，所以我们简单地求最值肯定用不出动态规划。

再举个例子：假设你们学校有 10 个班，你已知每个班的最大分数差（最高分和最低分的差值）。那么现在我让你计算全校学生中的最大分数差，你会不会算？可以想办法算，但是肯定不能通过已知的这 10 个班的最大分数差推到出来。因为这 10 个班的最大分数差不一定就包含全校学生的最大分数差，比如全校的最大分数差可能是 3 班的最高分和 6 班的最低分之差。

这次我给你提出的问题就不符合最优子结构，因为你没办通过每个班的最优值推出全校的最优值，没办法通过子问题的最优值推出规模更大的问题的最优值。前文 动态规划详解 说过，想满足最优子结，子问题之间必须互相独立。全校的最大分数差可能出现在两个班之间，显然子问题不独立，所以这个问题本身不符合最优子结构。

那么遇到这种最优子结构失效情况，怎么办？策略是：改造问题。对于最大分数差这个问题，我们不是没办法利用已知的每个班的分数差吗，那我只能这样写一段暴力代码：

int result = 0;
for (Student a : school) {for (Student b : school) {if (a is b) continue;result = max(result, |a.score - b.score|);}
}
return result;

改造问题，也就是把问题等价转化：最大分数差，不就等价于最高分数和最低分数的差么，那不就是要求最高和最低分数么，不就是我们讨论的第一个问题么，不就具有最优子结构了么？那现在改变思路，借助最优子结构解决最值问题，再回过头解决最大分数差问题，是不是就高效多了？

二、动态规划的基本框架（以斐波那契数列说明）

 ​​​​​​斐波那契数列：

 1. 穷举

 动态规划的本质就是穷举只是比暴力穷举更优一点而已

 有如下写法：

int fib(int N) {if (N == 1 || N == 2) return 1;return fib(N - 1) + fib(N - 2);
}

其递归树结构如下： 

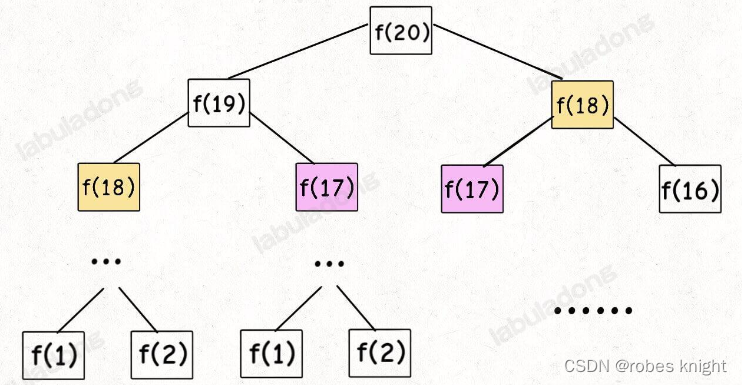
可以看出，效率很低，存在很多的重复计算 

2. 备忘录去重

 即然耗时的原因是重复计算，那么我们可以造一个「备忘录」，每次算出某个子问题的答案后别急着返回，先记到「备忘录」里再返回；每次遇到一个子问题先去「备忘录」里查一查，如果发现之前已经解决过这个问题了，直接把答案拿出来用，不要再耗时去计算了。

 代码如下：

int fib(int N) {// 备忘录全初始化为 0int memo[N + 1];memset(memo, 0, sizeof(memo));// 进行带备忘录的递归return dp(memo, N);
}// 带着备忘录进行递归
int dp(int memo[], int n) {// base caseif (n == 0 || n == 1) return n;// 已经计算过，不用再计算了if (memo[n] != 0) return memo[n];memo[n] = dp(memo, n - 1) + dp(memo, n - 2);return memo[n];
}

注意：可能你会疑问，每次只考虑第一次计算，能保证结果的最优吗

答案是可以，这是转移方程决定的，我们通过转移方程得到的结果就是局部最优，如果不是，那么就是转移方程写错了 

 递归树简化如下图：

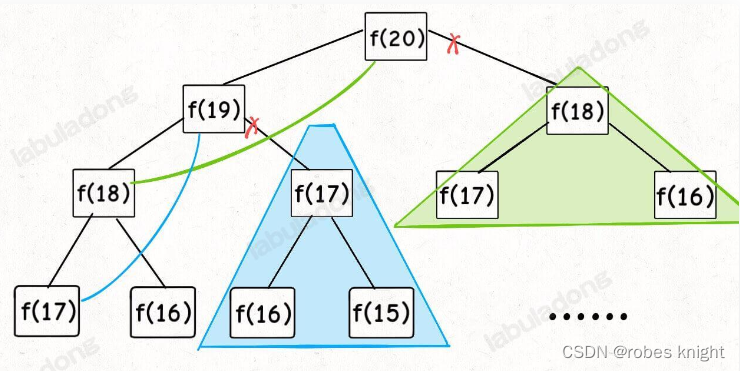
 这种备忘录的剪枝操作，其实相当于只留下有用的主干，上图可以进一步画为：

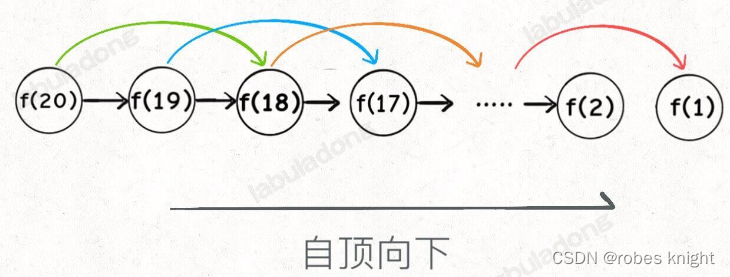
3. dp数组迭代求解

 有了上一步「备忘录」的启发，我们可以把这个「备忘录」独立出来成为一张表，通常叫做 DP table，在这张表上完成「自底向上」的推算

int fib(int N) {if (N == 0) return 0;int* dp = new int[N + 1];// base casedp[0] = 0; dp[1] = 1;// 状态转移for (int i = 2; i <= N; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[N];
}

状态转移如下： 

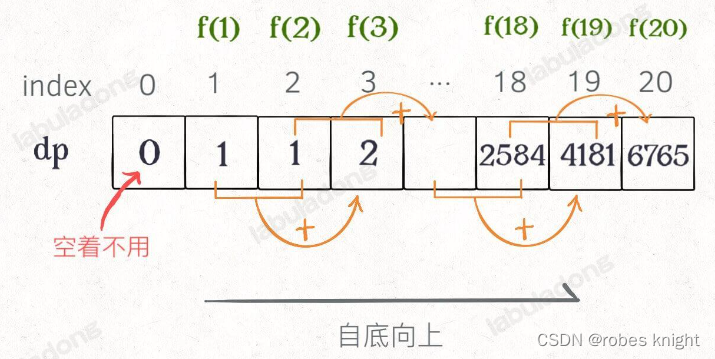
  我们发现和备忘录数组几乎一模一样，只是顺序不同

为什么可以将备忘录优化的递归写法转换为dp数组的迭代写法？

备忘录优化相当于去除重复的计算，每种计算只操作一次，而dp数组是先规划好要计算多少个状态，然后进行遍历，每种状态也只遍历一次，因此，两种写法本质上是一样的

注意：递归法使用备忘录去重后，尽管时间复杂度和迭代相同，但是，我们递归会不断的在栈上调用函数，造成大量的内存和时间消耗，这会导致实际运行时，递归法的时间空间消耗大于迭代法 

 详情参考：

第七章 C语言函数_递归函数的致命缺陷：巨大的时间开销和内存开销(附带优化方案)_c++ 递归资源消耗-CSDN博客

三、dp数组迭代五部曲

1.明确dp数组下标和下标对应的值的含义

这一步其实是要和转移方程结合理解的，很多时候我们是为了能够写出转移方程，才进行某种dp数组的定义

所以这一步非常重要，我们需要知道问题中有哪些状态才能为dp数组合理分配这些状态

所谓状态，也就是原问题和子问题中会变化的变量。我们要将这些变化的量分配给dp数组的下标和值

注意：比较难的题，状态不能一眼看出来，需要我们自己进行构造，这样的题只有靠积累

（1）简单例子

1：斐波那契的dp[]定义：i 表示n = i，dp[i]表示n = i对应的结果是什么，这样的逻辑非常清晰

2：凑零钱：（注意虽然硬币个数不会变化，因为硬币数量无限，所以有两个变化量，凑零钱的硬币数和目标金额），所以我们定义i为目标金额，dp[i]值为零钱个数（一般都会吧dp[i]当作输出结果）

这里会有一点歧义 ，我们要知道我们最后要得到的是什么，应该是amount对应的最小数量，那么dp[i]应该设置为金额i对应的最小数量，不要思考成我们将dp[i]定义为i对应的所有数量，然后通过比较所有dp[i]来求得最小值，这样似乎更容易理解，但是却不实际，那样dp[i]会被定义为二维数组，复杂度也上升了

我们应该知道，最小这个限制，是在转移方程里面实现的，所以我们默认得到的dp[i]就是最小值！

（2）困难例子

最长递增子序列：我们发现问题中貌似没有直接给出变化的状态，从而无从下手

这是子序列问题中的一类问题，处理方法有相对固定几类，我们这里就直接套用经典定义

dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度。

对于其他不明确状态的问题如何定义，这个也要靠积累，需要我们多做题才知道

虽然说了这么多，但是实际情况是要背住不同题型的数组含义，现想根本来不及

2.确定递推公式（转移方程）

动态规划的核心设计思想是数学归纳法。

相信大家对数学归纳法都不陌生，高中就学过，而且思路很简单。比如我们想证明一个数学结论，那么我们先假设这个结论在 k < n 时成立，然后根据这个假设，想办法推导证明出 k = n 的时候此结论也成立。如果能够证明出来，那么就说明这个结论对于 k 等于任何数都成立。

类似的，我们设计动态规划算法，不是需要一个 dp 数组吗？我们可以假设 dp[0...i-1] 都已经被算出来了，然后问自己：怎么通过这些结果算出 dp[i]？

直接拿最长递增子序列这个问题举例你就明白了。不过，首先要定义清楚 dp 数组的含义，即 dp[i] 的值到底代表着什么？

我们的定义是这样的：dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度（子序列中要包含nums[i],可能我们会想这样不能找到实际的最大子序列，但是其实我们遍历了所有nums[i]，并不会漏掉）。

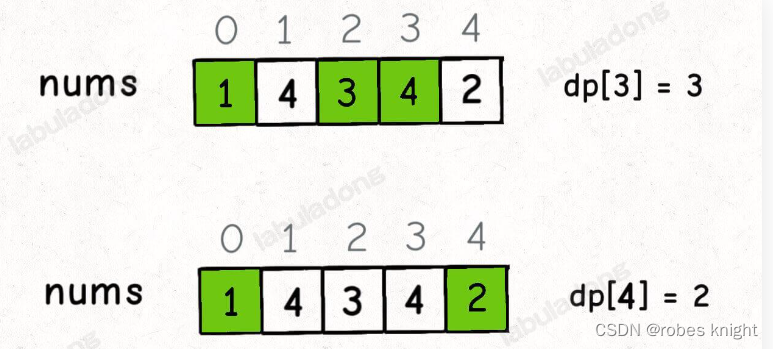
假设我们已经知道了 dp[0..4] 的所有结果，我们如何通过这些已知结果推出 dp[5] 

这就是求解转移方程的重点一步，此处

根据刚才我们对 dp 数组的定义，现在想求 dp[5] 的值，也就是想求以 nums[5] 为结尾的最长递增子序列。

其实就是自己总结规律，然后使用数学归纳法验证

光靠脑袋想dp的递推公式确实很困难 我的做法是画一个dp数组出来 找一个例子填进去,然后通过观察找出规律倒推递推公式(仅供参考,有待验证)

当我们发现递推公式不好找时,需要思考是否改变dp定义

nums[5] = 3，既然是递增子序列，我们只要找到前面那些结尾比 3 小的子序列，然后把 3 接到这些子序列末尾，就可以形成一个新的递增子序列，而且这个新的子序列长度加一。

同时我们是在找最长的子序列，所以我们需要找出前面序列中的最长序列接上去

我们的转移方程为：

dp[i] = dp[j] + 1;//j是比i小的数

 接下来就是要将取最大值还有求比i小的j结合起来

代码如下：

    for(int j = 0;j < i;j++){        if (nums[i] > nums[j]) {// 把 nums[i] 接在后面，即可形成长度为 dp[j] + 1，// 且以 nums[i] 为结尾的递增子序列dp[i] = Math.max(dp[i], dp[j] + 1);}}

这整个代码才是完整的转移方程 

一个重点：

我们一定要假设已经知道了dp[i-1]，并且我们设置的dp数组可以存放的值就是我们希望的值

3. dp数组初始化和base case

初始化要结合我们对dp数组的定义进行设置，并且结合保证在执行max和min操作时不会影响更新值，对dp数组的定义不同的话，初始化也会有差别

base case 就是递归中的最底层，是所有子问题中的最基础的问题，靠这个问题推出其他所有解

初始化非常重要，它和转移方程共同决定了我们定义的dp[i]里面的值是否正确,一般是确定了dp定义和转移方程,再开始初始化

 一个方法：

我们只需要把dp数组画出来，然后看看是是通过什么方向进行转移的，将这个方向的最开头的状态初始化即可

4. 确定遍历顺序

现在接触到的都是顺序进行遍历的，并没有在遍历时挖坑，但是后面有从前往后，从后往前还有斜着遍历

这个也需要把dp数组画出来，然后一步步观察状态如何转移，不同顺序可能会导致转移的先后发生变化

将转移方程放入遍历中：

        for(int i = 0;i < nums.size();i++)for(int j = 0;j < i;j++){if(nums[i] > nums[j]){dp[i] = max(dp[i],dp[j]+1);}}

5. dp数组打印

通过递推公式手写出dp数组，用于检测dp哪里写错了

四、举例说明

1. 零钱兑换

题目链接：322. 零钱兑换 - 力扣（LeetCode）

(1)dp定义:

首先确定状态，问题中改变的状态只有总金额和使用的硬币个数（硬币总数无限，所以剩下的硬币数量不变化）

我们将dp[i]和i与变化量进行匹配，从而有如下设置：

i为总金额。dp[i]为达到总金额i需要的硬币数量

(2)转移方程

我们这样想，肯定是要建立dp[i]和dp[j]的联系，但实际这个i j应该如何取，也就是总金额如何变化更合理，所以自然想到了，每次对总金额 i 减少一个硬币的值，来求得 j ，那么关系如何建立呢

这就要用到上面的数学归纳法了，假设我们已经知道减少一个硬币后的dp[i - coin]的值，那么dp[i]的最小值就是dp[i - coin]+1

(3)初始化

由于我们的i要索引到amount，索引dp的size要为amount+1，同时对于dp[i]来说，最差的情况即使由i个一元硬币组成，那么最大个数为i，为了使得初始状态不影响结果，需要将dp[i] 赋值 i+1，为了省事直接赋值最大的amount+1，代码如下：

vector<int> dp(amount+1,amount+1);

对于base case，我们知道dp[0] = 0，但是注意dp[1] != 1,因为有一个硬币但不一定是一个一元的硬币，所有可能dp[1] = -1,因此不能将dp[1]放入base case中，代码如下：

        dp[0] = 0;// dp[1] = 1;

(4)确定遍历方向:

此题为顺序遍历，但是也要仔细理解一下

非常类似bfs的理解过程，我们先对dp[i]中所有金额从0-amount进行遍历，保证能够处理到所有的i（类似于走通每一层），然后对于每一个i我们都将所有的coin去除一次（所有的选择都选一次），选出最小的情况然后赋值给dp[i]

代码如下：

        for(int i = 0;i < amount+1;i++)for(int coin : coins){if(i - coin < 0)continue;dp[i] = min(dp[i],dp[i - coin] + 1);}

(5)：打印dp数组进行debug，此题过程比较简单就不演示了

完整代码如下：

class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount+1,amount+1);if(amount == 0)return 0;dp[0] = 0;// dp[1] = 1;for(int i = 0;i < amount+1;i++)for(int coin : coins){if(i - coin < 0)continue;dp[i] = min(dp[i],dp[i - coin] + 1);}return dp[amount] == amount+1 ? -1 : dp[amount];}
};

2. 斐波那契数列

题目链接：509. 斐波那契数 - 力扣（LeetCode）

此题已经给出转移方程，并且dp数组的定义也较为清楚，base case给出，初始化时没有特殊要求，我们直接初始化为0就行了，并且也是顺序遍历，所有很容易写出如下代码：

class Solution {
public:int fib(int n) {if(n==0) return 0;vector<int> dp(n+1,0);dp[0] = 0;dp[1] = 1;for(int i = 2;i <= n;i++)dp[i] = dp[i-1] +dp[i-2];return dp[n];}
};

由于只涉及到两个数的处理，所以我们可以只保留这两个数，有如下优化代码：

class Solution {
public:int fib(int n) {if(n==0)return 0;if(n==1)return 1;int p=0,q=1,res=0;for(int i = 2;i <= n;i++){res = p + q;p = q;q = res;}return res;}
};