01.基于奇异值分解(SVD)去噪原理

奇异值分解（Singular Value Decomposition, SVD）是线性代数中一种重要的矩阵分解方法，它可以用于信号处理、图像去噪、数据压缩等多种应用。在图像去噪的过程中，SVD可以用来分离图像中的信号和噪声，通过对奇异值进行阈值处理的方式来实现去噪的效果。

基于奇异值去噪的方法通常分为如下几个步骤：

1. 对给定的数据（例如图像）进行SVD分解，得到奇异值矩阵和对应的奇异向量。

2. 根据设定的阈值方法修改奇异值矩阵，一般是将小于阈值的奇异值置为零。

3. 使用修改后的奇异值矩阵和原始的奇异向量重新构造数据（图像），以此实现去噪。

在选择阈值的过程中，可以根据不同的标准确定阈值，以下是您提到的三种方法：

（一）阈值设为奇异值突变的值：在这种方法中，需要观察奇异值分布图，寻找到奇异值发生突变（即从较大的值突然下降到较小的值）的地方，选择这个点作为阈值。突变点之前的奇异值通常对应于图像的主要信号，而突变点之后的奇异值则主要对应于噪声。

（二）阈值设为奇异值的中值：这种方法中，阈值被设为所有奇异值的中值（中位数）。相对于其他方法，中值对异常值不敏感，可能有助于保持图像某些重要特征，并去除噪声。

（三）阈值设为奇异值的平均值：在这种方式下，阈值被设定为所有奇异值的平均值。平均值往往会受到较大奇异值的影响，所以如果信号中包含有较强的成分，那么平均值设定的阈值可能较高，可能会导致一些较弱的信号部分也被当做噪声去除掉。

在实际应用中，选择阈值的方法需要根据具体任务、数据的特点和噪声的性质来确定，可能需要实验确定最佳阈值。有时候还会采用更加复杂的阈值选择方法，如基于统计特性的阈值选择方法（例如基于导数或高斯混合模型等）。

02.代码的效果图

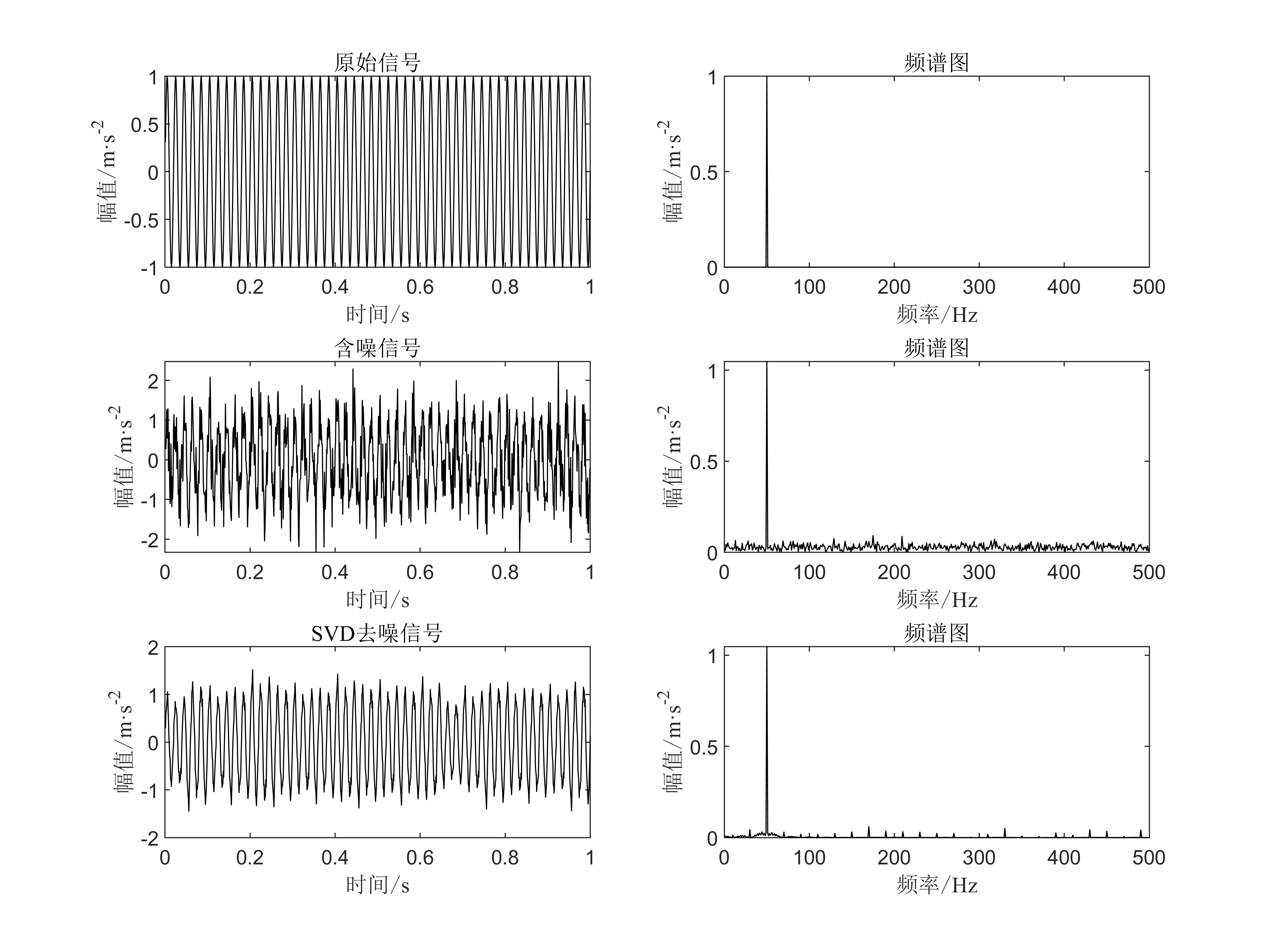
获取代码请关注MATLAB科研小白的个人公众号（即文章下方二维码），并回复：SVD

本公众号致力于解决找代码难，写代码怵。各位有什么急需的代码，欢迎后台留言~不定时更新科研技巧类推文，可以一起探讨科研，写作，文献，代码等诸多学术问题，我们一起进步。