聚簇索引

特点：

• 索引和数据保存在同一个B+树中

• 页内的记录是按照主键的大小顺序排成一个单向链表 。

• 页和页之间也是根据页中记录的主键的大小顺序排成一个双向链表 。

• 非叶子节点存储的是记录的主键+页号。

• 叶子节点存储的是完整的用户记录。

优点：

• 数据访问更快 ，因为索引和数据保存在同一个B+树中，因此从聚簇索引中获取数据比非聚簇索引更快。
• 聚簇索引对于主键的排序查找和范围查找速度非常快。
• 按照聚簇索引排列顺序，查询显示一定范围数据的时候，由于数据都是紧密相连，数据库可以从更少的数据块中提取数据，节省了大量的IO操作 。

缺点：

• 插入速度严重依赖于插入顺序 ，按照主键的顺序插入是最快的方式，否则将会出现页分裂，严重影响性能。因此，对于InnoDB表，我们一般都会定义一个自增的ID列为主键。
• 更新主键的代价很高 ，因为将会导致被更新的行移动。因此，对于InnoDB表，我们一般定义主键为不可更新。

限制：

• 只有InnoDB引擎支持聚簇索引，MyISAM不支持聚簇索引。
• 由于数据的物理存储排序方式只能有一种，所以每个MySQL的表只能有一个聚簇索引。
• 如果没有为表定义主键，InnoDB会选择非空的唯一索引列代替。如果没有这样的列，InnoDB会隐式的定义一个主键作为聚簇索引。
• 为了充分利用聚簇索引的聚簇特性，InnoDB中表的主键应选择有序的id，不建议使用无序的id，比如UUID、MD5、HASH、字符串作为主键，无法保证数据的顺序增长。

非聚簇索引

（二级索引、辅助索引）

聚簇索引，只能在搜索条件是主键值时才发挥作用，因为B+树中的数据都是按照主键进行排序的，如果我们想以别的列作为搜索条件，那么需要创建非聚簇索引。

例如，以c2列作为搜索条件，那么需要使用c2列创建一棵B+树，如下所示：

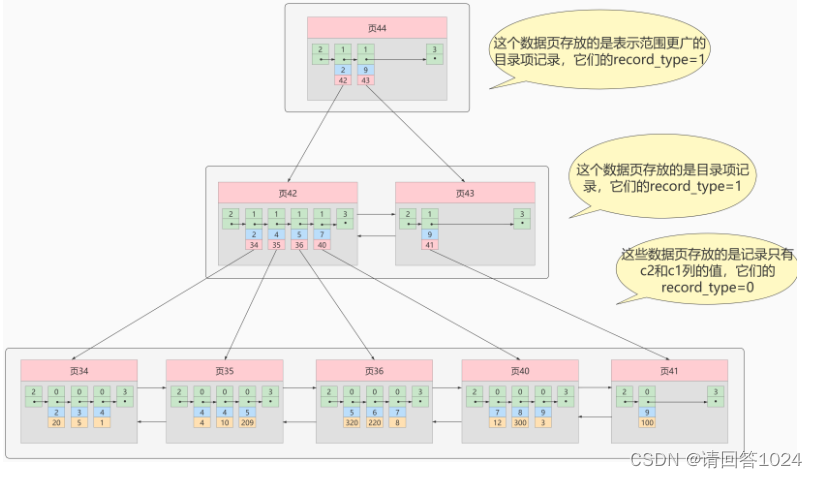
这个B+树与聚簇索引有几处不同：

• 页内的记录是按照从c2列的大小顺序排成一个单向链表 。

• 页和页之间也是根据页中记录的c2列的大小顺序排成一个双向链表 。

• 非叶子节点存储的是记录的c2列+页号。

• 叶子节点存储的并不是完整的用户记录，而只是c2列+主键这两个列的值。

B+树中聚簇索引的查找（匹配）逻辑

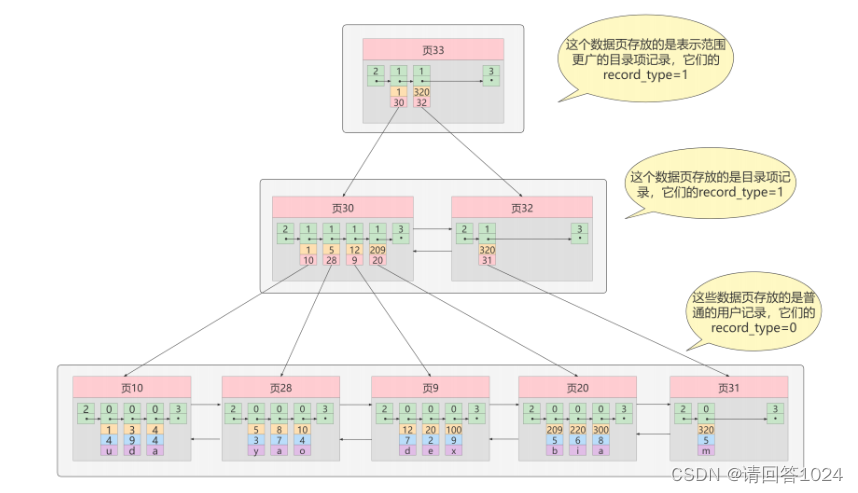
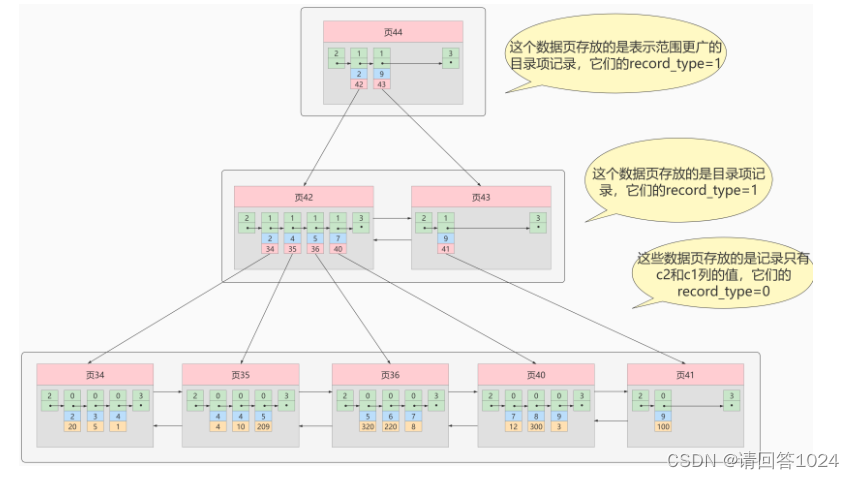
B+树中非聚簇索引的查找（匹配）逻辑

例如： 根据c2列的值查找c2=4的记录，查找过程如下：

1. 根据根页面44定位到页42（因为2 ≤ 4 < 9）
2. 由于c2列没有唯一性约束，所以c2=4的记录可能分布在多个数据页中，又因为 2 ≤ 4 ≤ 4，所以确定实际存储用户记录的页在页34和页35中。
3. 在页34和35中定位到具体的记录。
4. 但是这个B+树的叶子节点只存储了c2和c1（主键）两个列，所以我们必须再根据主键值去聚簇索引中再查找一遍完整的用户记录。
5. like 张%