递归算法练习

递归算法是所有算法中较难的一种，依靠他代码的简洁和清晰地逻辑很受人们喜欢，但是新手入门递归还是会被他不同寻常的思路吓到，其实面对递归问题我们只需要看清题目，分析出要求，有清晰的解题思路，只要仔细分析，就会很简单的解决问题。
提到递归，大多数题目就都离不开二叉树，这只不过是其中的一种，我们来做一做其他类型的题目，提高我们分析递归问题的逻辑能力和分析能力，由浅入深，从而掌握递归。
第一题
合并两个有序链表
在这里插入图片描述
这道题我们可以搞一个虚拟节点，很容易就能解决这道问题。
但是如果我们用递归的方法去解决这道题目，我们需要思考递归的每一步需要做什么，将一个大问题划分为数个小问题来解决。
递归需要我们做什么呢？给定两个链表，将他们合并，然后返回头节点。
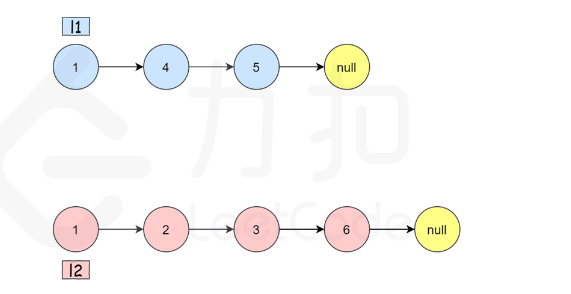
在这里插入图片描述
我们判断两个链表的首元素后，假设是list1的val大于list2的val，就向后连接list2的节点，此时剩下的工作就是连接list1的节点和list2的剩余节点，就是list1和list2剩余节点的合并问题，切记我们呢还需要返回头节点。
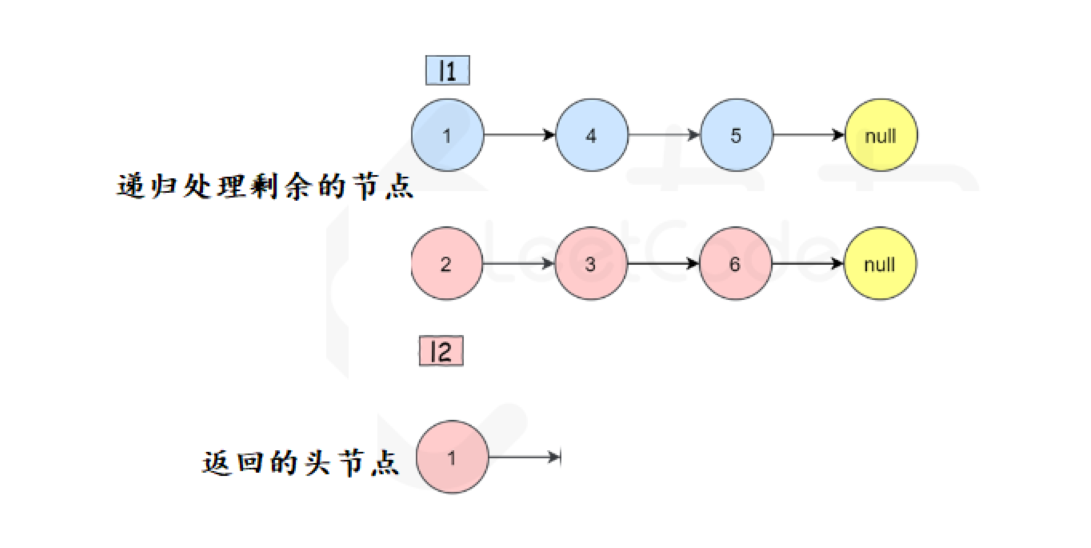
在这里插入图片描述
递归问题还需要判断的就是何时结束，这道题目就是判断一方如果是空节点，就直接将另一方的节点连接起来就好。

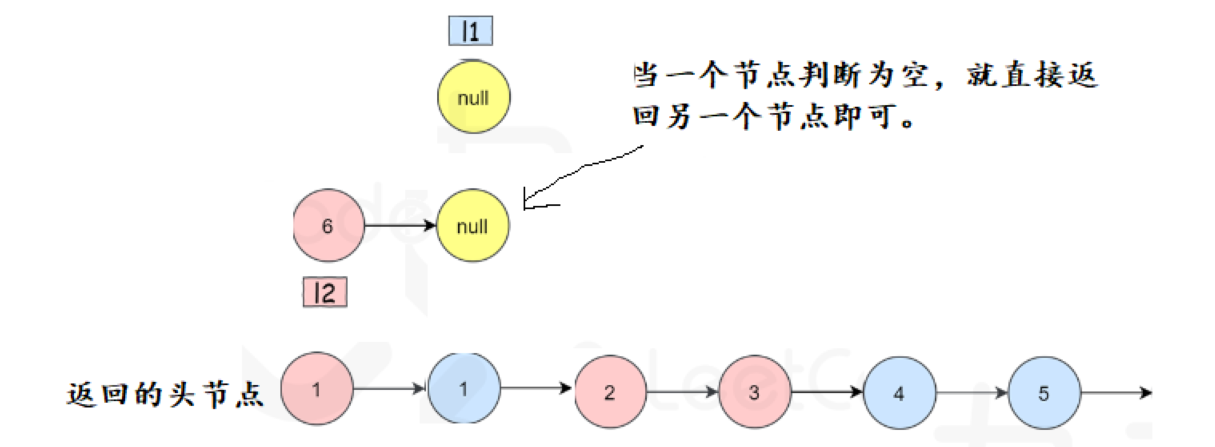
因为我们返回的是头节点，所以每次只需要将他们连接起来即可。这个操作就是使前边的节点的next等于后续返回的头节点，这样就将两个链表的节点全部连接起来了。
代码如下

class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {if(list1==nullptr)//遇到空节点就返回另一个节点的头指针{return list2;}if(list2==nullptr){return list1;}if(list1->val>list2->val){list2->next=mergeTwoLists(list1,list2->next);//接收返回的节点并链接return list2;}else{list1->next=mergeTwoLists(list1->next,list2);return list1;}}
};

第二题
反转链表
在这里插入图片描述
这道题如果直接来做的话，使用一个虚拟头节点，然后定义一个节点指针一直头插就可以解决，或者就是设置三个指针变量，从前往后依次改变指针的方向。
头插法

ListNode* reverseList(ListNode* head) {ListNode* newnode=new ListNode;ListNode*cur=nullptr;while(head!=nullptr){newnode->next=head;ListNode* next=head->next;//保留下一个节点，防止下一步操作导致链表断开head->next=cur;cur=head;head=next;}return newnode->next;}

直接改变结点指针的方法

class Solution {
public:ListNode* reverseList(ListNode* head) {ListNode* prev = nullptr;ListNode* curr = head;while (curr) {ListNode* next = curr->next;curr->next = prev;prev = curr;curr = next;}return prev;}
};

如果使用递归的思想来解决这道问题，我们呢还是需要考虑递归的每一步是要做什么。
我们需要将这个问题拆分为几个小问题来解决，不仅需要改变所有节点的指向，还要将链表的头节点返回回来。
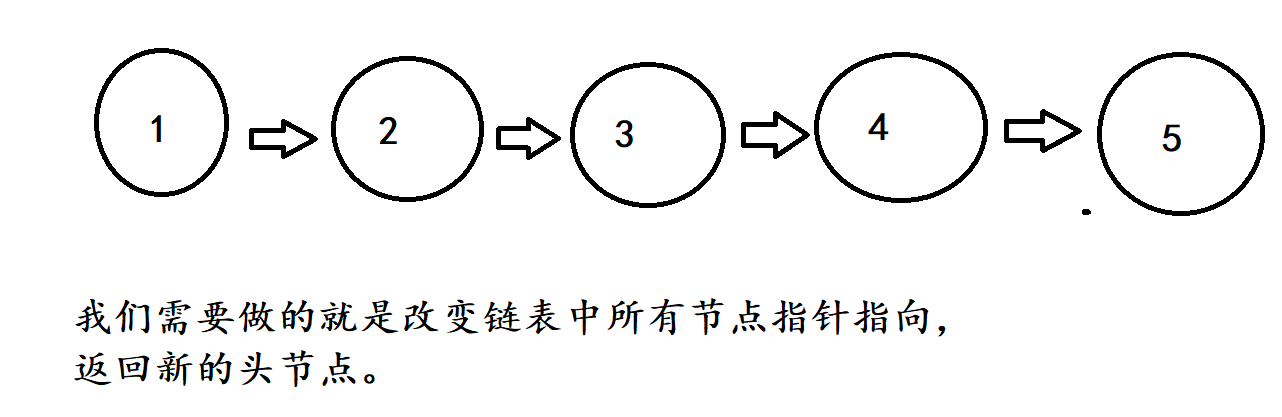
在这里插入图片描述
拆分成子问题，一直遍历到最后一个节点，将该节点返回，递归过程中不仅要将新的头节点层层返回回去，还要改变指针指向。

代码如下

ListNode* reverseList(ListNode* head) {if(head==nullptr||head->next==nullptr){return head;}ListNode* newnode=reverseList(head->next);//接收返回值head->next->next=head;//改变指针指向head->next=nullptr;//统一处理return newnode;//层层递归返回新的头节点}

第三题
两两交换链表中的节点

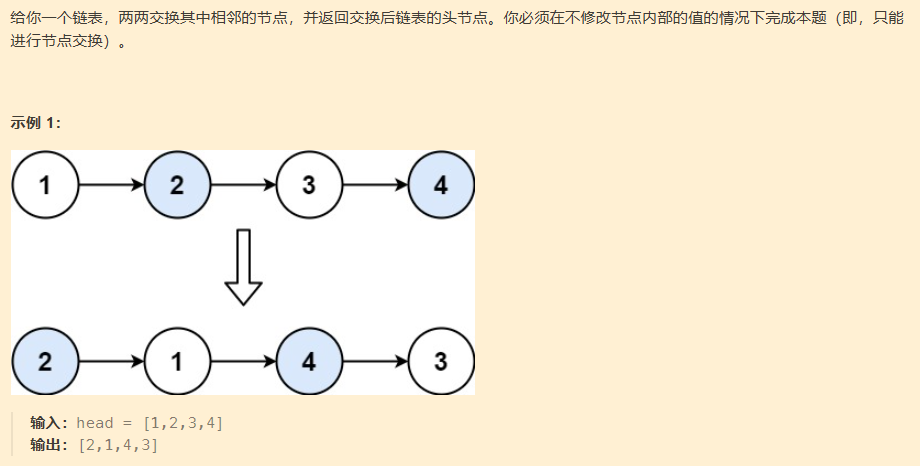
在这里插入图片描述
这道题要求我们不是修改链表的节点中存放的值，使用递归算法解决，还是要拆分问题。将一个大的问题拆分为小的子问题。
单看每一步，我们需要做的是将两个节点翻转，返回新的头结点，至于递归结束的条件，很明显，如果只有一个节点或者节点为空就直接返回该节点即可。因为如果是空，就直接链接上了，如果只有一个节点，这个节点的next为空，依然成立。
现在就是如何翻转两个节点并且返回新节点的问题了。如图
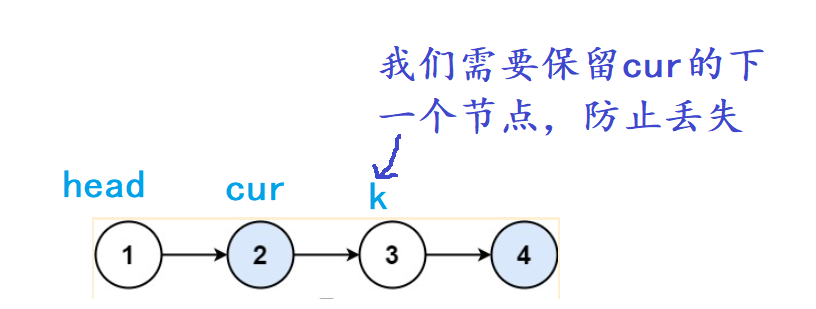
在这里插入图片描述
接下来就是改变head和cur的next的指向，因为我们已经保留k节点的指针了，所以cur的next可以放心修改，然后就是接受返回值。

在接下来的子问题中，做同样的步骤，翻转3,4节点，返回新的头结点，此时上一次递归的next指针就可以接收这个返回值，将链表连接起来。

代码如下

class Solution {
public:ListNode* swapPairs(ListNode* head) {ListNode* newnode=nullptr;if(!(head&&head->next)){return head;}ListNode*cur=head->next;ListNode*k=cur->next;head->next=swapPairs(k);cur->next=head;return cur;}
};

第四题
在这里插入图片描述
这道题让我们求x的n次幂，题目介绍很简单，这道题我们也可以直接使用库里面的函数直接解决，但是这样就体现不出这道题的意义了，来尝试一下用递归的方法解决这个问题。
首先来说直接算的话为什么不好呢？
就比如2的8次方，我们再已经知道2的4次方是多少之后，我们可以只使用一次乘法就得出结果，但是如果一步一步算，我们还要再乘4次才能得到相应的结果。
所以我们在求x的n次方时，可以先求出x的n/2次方，然后让他们想乘就可以了。我们写一个pow函数帮助我们实现这个功能。
此时会出现两个问题
如果是奇数怎么办？递归出口应该是怎么样的呢？举例来分析一下

2⁹ 需要计算的话，因为是奇数，所以再最后返回两个2⁴时，还要再乘以一个2。
求2⁴时，结果是两个2^2相乘。
求2²时，此时为两个2相乘。如果递归的过程中，n等于1时，就直接返回x即可。

还要注意，n有可能是负数，所以如果n为负数，就直接用1除以返回的结果，在传递参数时将n变为-n即可。

还要注意n为0的情况，我们返回1就可以了。

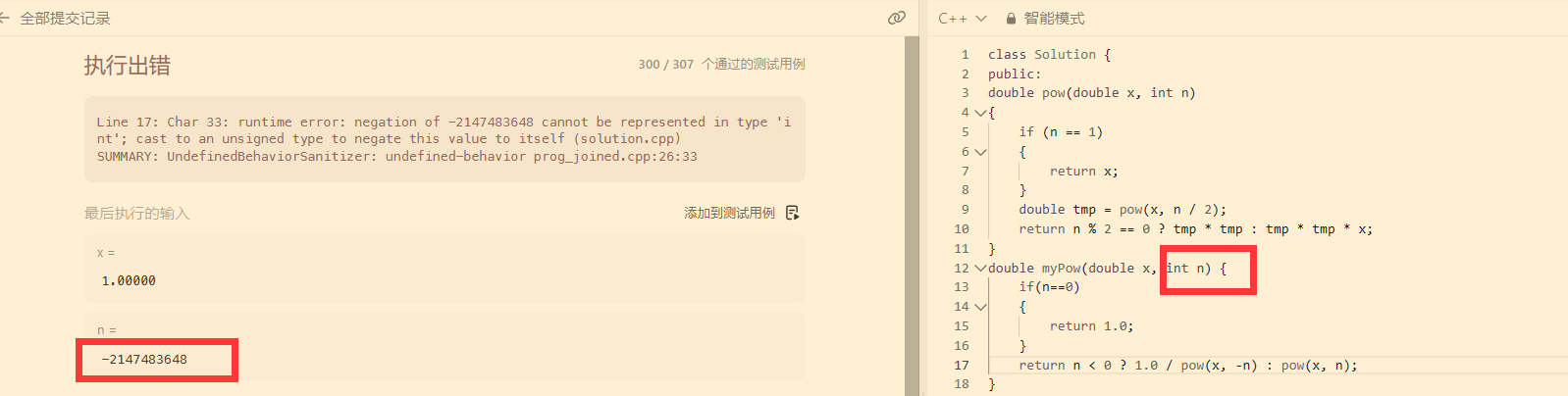
在这里插入图片描述

这道题还会出现数据溢出的情况，我们可以将n的类型写为long long就可以解决。
代码如下

double pow(double x, long long n)
{if (n == 1){return x;}double tmp = pow(x, n / 2);return n % 2 == 0 ? tmp * tmp : tmp * tmp * x;
}
double myPow(double x, int n) {if(n==0){return 1.0;}return n < 0 ? 1.0 / pow(x, -(long long)n) : pow(x, n);
}