点击下载本文软件(5积分):
https://download.csdn.net/download/beijinghorn/89071073![]() https://download.csdn.net/download/beijinghorn/89071073
https://download.csdn.net/download/beijinghorn/89071073
百度网盘(不需积分):
https://pan.baidu.com/s/1FwCsSzORm4YKow3eVi-u5w?pwd=rq14![]() https://pan.baidu.com/s/1FwCsSzORm4YKow3eVi-u5w?pwd=rq14
https://pan.baidu.com/s/1FwCsSzORm4YKow3eVi-u5w?pwd=rq14

一、文件夹LastWriteTime
我们在Windows资源管理器中看到的文件夹时间,是什么时间呢?

按微软的解释,应该是该文件夹的最后写入(修改)的时间,称为 LastWriteTime。
DirectoryInfo root = new DirectoryInfo(@"c\root");DateTime ft = root.LastWriteTime;LastWriteTime 是 DirectoryInfo 的 get set 的属性;既可以获取 文件夹的最后写入时间,也可以设置这个时间。
那么,这个最后写入时间是什么时间呢?怎么算出来的?
一般理解,这个时间应该是该文件夹下,所有文件的,最后写入时间。
没错!一般情况下确实如此。
但是,世界的问题就在于没有一般情况。
你所看到这个时间,并不是真正的最后时间!一旦,文件夹或文件夹下的文件、子目录有复制、删除、移动、创建等等操作,文件夹的时间 一般情况下 就不对了!
这会在文件整理的时候,造成一些困惑。
咱们的期望是:这个时间能体现下面所有文件的最后写入(修改)时间。
让我们一起动手写一个小工具实现这个期望吧。
二、文件夹LastWriteTime的算法
需要考虑两种情况:
(1)文件夹下有文件
LastWriteTime = LastOf(All files LastWriteTime);
所有文件中的最新写入时间。
(2)如果文件夹下,没有任何文件,但又有子目录。
LastWriteTime = LastOf(All Valid Sub-Directory)
所有有效子目录的最新写入时间。
有效子目录是指含有文件的子目录或下级含有文件的子目录。
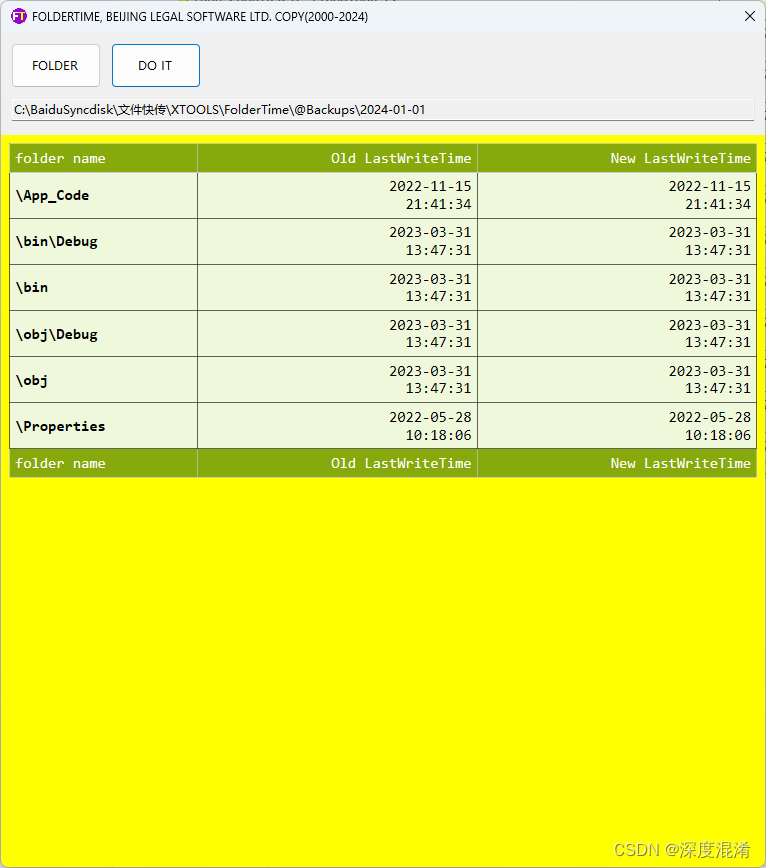
三、文件夹时间整理工具
欢迎界面
选定文件夹

重置时间









)








)

