随着信息技术的快速发展,数字乡村建设已成为推动农村高质量发展的重要引擎。数字乡村通过科技创新,不仅改变了传统农业生产方式,也提升了乡村治理水平,为农民带来了更加便捷的生活。本文将从数字乡村的内涵、科技引领农村高质量发展的路径、取得的成效以及面临的挑战与未来展望等方面,探讨数字乡村的创新之路。

一、数字乡村的内涵与意义
数字乡村,是指利用现代信息技术手段,对乡村经济社会发展的各个环节进行数字化改造和智能化升级,实现乡村产业的数字化转型、乡村治理的智能化升级以及乡村生活的智慧化提升。数字乡村建设不仅有助于提升农业生产效率和质量,推动农村产业结构的优化升级,还能改善农民生活质量,促进乡村社会的和谐稳定。
科技作为数字乡村建设的核心驱动力,为农村高质量发展提供了有力支撑。通过引入物联网、大数据、云计算、人工智能等现代信息技术,可以实现农业生产的精准化、智能化管理,提高农业资源利用效率;可以优化乡村治理流程,提升政府决策的科学性和精准性;可以推动农村电商、乡村旅游等产业的发展,拓宽农民增收渠道。
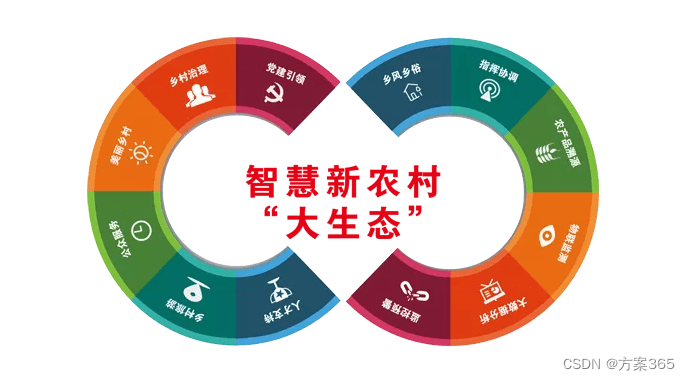
二、科技引领农村高质量发展的路径
(一)加强农业科技创新,推动农业现代化
农业是农村高质量发展的基础。要加强农业科技创新,推广智能化农业装备和技术,提高农业生产效率和质量。通过建设智慧农业示范区,推广精准种植、智能灌溉、无人机植保等先进技术,降低农业生产成本,提高农产品附加值。同时,加强农业科技人才培养,为农业现代化提供智力支持。

(二)推进乡村治理智能化,提升乡村治理水平
乡村治理是农村高质量发展的保障。要利用大数据、人工智能等技术手段,推进乡村治理智能化。通过建设乡村综合信息服务平台,实现政务服务、公共服务等事项的在线办理和查询,提高政府服务效率。同时,利用智能化手段加强乡村社会治安管理,提高乡村社会治理的精准性和有效性。

(三)发展农村数字经济,培育乡村发展新动能
数字经济是农村高质量发展的新引擎。要大力发展农村电商、数字农业、乡村旅游等数字经济产业,拓宽农民增收渠道。通过建设农村电商服务平台,推动农产品上行和工业品下行,促进农村消费市场的繁荣。同时,结合当地特色资源,发展乡村旅游和数字文化产业,提升乡村经济的综合效益。
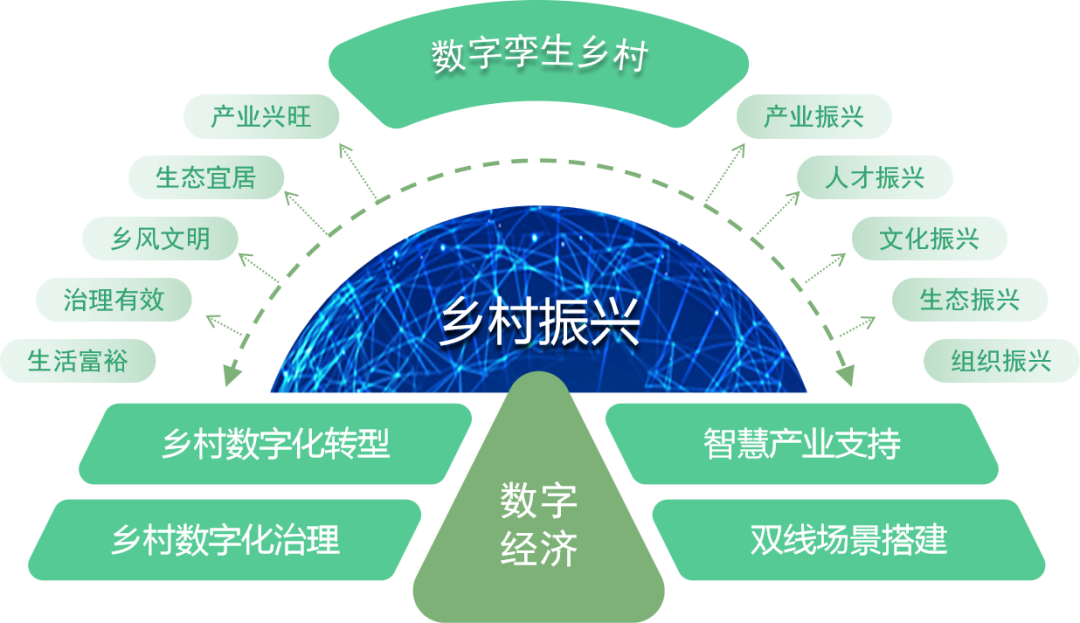
(四)加强基础设施建设,夯实数字乡村发展基础
基础设施是数字乡村建设的重要支撑。要加强农村信息基础设施建设,提高农村地区的网络覆盖率和数据传输速度。同时,加强农村交通、水利、电力等基础设施建设,为数字乡村发展提供有力保障。
三、数字乡村建设取得的成效
通过一系列科技创新举措的实施,数字乡村建设已经取得了显著成效。农业生产效率和质量得到了显著提升,农民收入水平和生活质量也得到了明显改善。乡村治理水平和政府服务效率得到了有效提升,乡村社会更加和谐稳定。同时,农村数字经济产业的蓬勃发展,为乡村经济注入了新的活力。
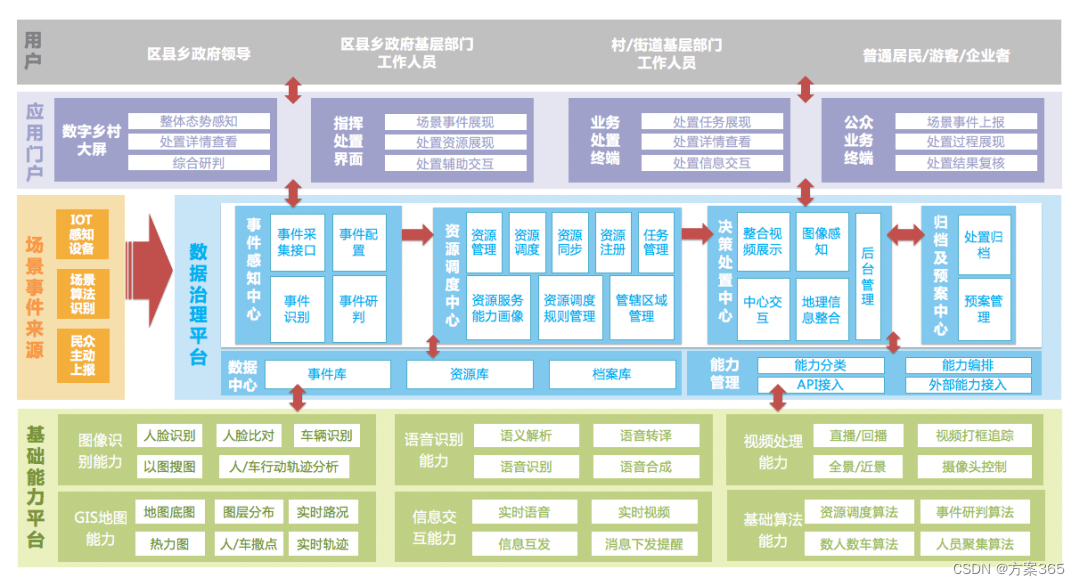
四、面临的挑战与未来展望
尽管数字乡村建设已经取得了显著成效,但仍面临着一些挑战。如农村信息化水平相对较低,数字技术应用不够广泛;农村数字人才匮乏,制约了数字乡村的发展;数字乡村建设投入不足,影响了建设的速度和质量等。
面对这些挑战,我们需要进一步加强科技创新和人才培养,提高数字乡村建设的质量和效益。同时,加大政策扶持和资金投入力度,为数字乡村建设提供有力保障。未来,随着数字技术的不断创新和应用领域的不断拓展,数字乡村将在更多领域实现深度融合和创新发展。农业生产将更加智能化、精准化,乡村治理将更加科学化、民主化,农民生活将更加便捷、舒适。数字乡村将成为推动农村高质量发展的重要力量,为实现乡村全面振兴和农业农村现代化奠定坚实基础。
五、结语
数字乡村创新之路是科技引领农村实现高质量发展的必然选择。我们要以科技创新为核心驱动力,加强农业科技创新、推进乡村治理智能化、发展农村数字经济、加强基础设施建设等方面的工作,不断推动数字乡村建设的深入发展。同时,我们也要正视数字乡村建设面临的挑战和问题,积极寻求解决方案和对策措施,为数字乡村的可持续发展提供有力保障。

“方案365”全新整理数字乡村-智慧农业、智慧城市、数据治理、智慧应急、数字孪生、乡村振兴、智慧乡村、元宇宙、数据中台、智慧园区、智慧矿山、城市生命线、智慧水利、智慧校园、智慧工地、智慧农业、智慧旅游等300+行业全套解决方案。
总之,数字乡村建设是推动农村高质量发展的重要途径和有效手段。我们要紧紧抓住数字乡村建设的机遇和挑战,加强科技创新和人才培养,推动数字技术与农业农村的深度融合和创新发展,为实现乡村全面振兴和农业农村现代化贡献智慧和力量。







)








)


目标跟踪中参数估计(似然、贝叶斯估计)理论知识)