前言
有个人跟我说浮点数运算起来非常麻烦,总是算着算着丢失精度,导致计算结果取int的时候取不准。毕竟系统也没有自动根据这个数的精度四舍五入的功能。
比如int(2.999999999999999)=2,但是float(2.999999999999999)=3.000000。
我觉得这个问题很好解决,正好网上一搜这个问题的答主并没有给出完整且正常的代码,只提到了可以用“round”处理,或者自己手搓了一个round,让我震撼。所以我就简单写了一下这篇博客。
文章目录
- 前言
- 小数点后n位取整的思路
- 思路1 利用round
- 思路实现
- 思路的优势和问题
- 思路2 利用字符串相关函数处理
- 思路实现
- 思路优势和问题
- 思路3 利用float降低精度
- 思路实现
- 思路优势和问题
小数点后n位取整的思路
思路1 利用round
思路实现
- round这个函数在这个问题里的作用:round只能对小数点后面那一位做四舍五入,没办法舍入第n位。但是我们可以利用这个特性去做。
- 直观的思路简述:
int(float(val,n),10),意思是取n位小数的val的值,然后转成int,从而完成满足n精度要求的int整型转换。
代码我让gpt给我写了一下:
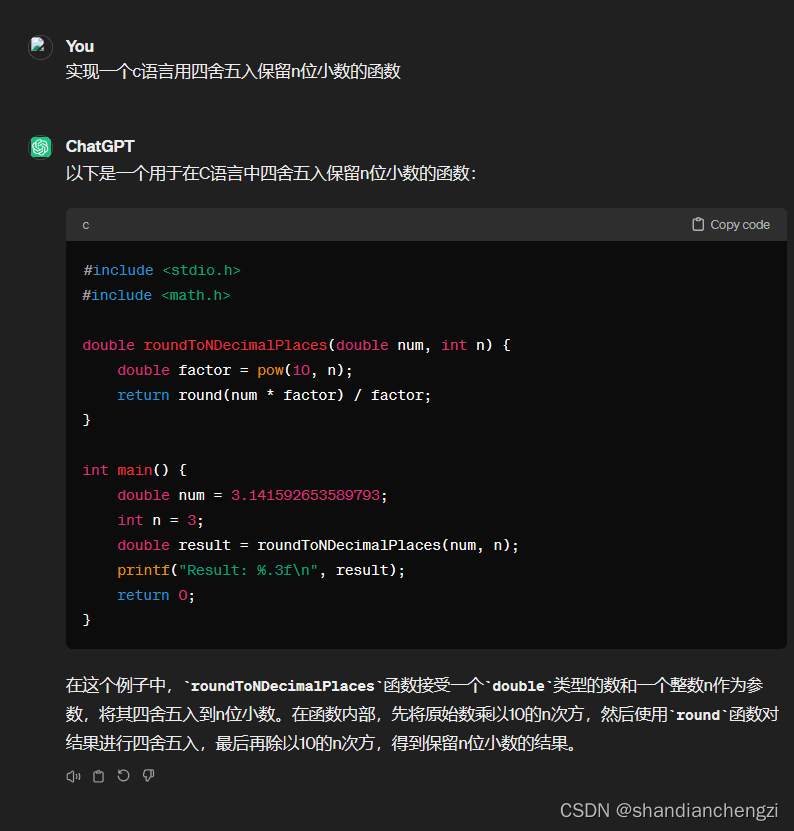
可用的代码如下:
#include <stdio.h>
#include <math.h>double roundToNDecimalPlaces(double num, int n) {double factor = pow(10, n);return round(num * factor) / factor;
}int main() {double num = 9.99999999;int n = 3;double result = roundToNDecimalPlaces(num, n);printf("Result: %.3f\n", result);return 0;
}编译方式(需要通过在编译命令中添加 -lm 选项来链接数学库):
gcc test_round.c -o test_round -lm
运行结果就是Result: 10.000。
当然,你如果希望简洁一点,也可以把代码写成:int(round(val*pow(10,n)/pow(10,n)))。
思路的优势和问题
优势:能实现n位存储精度。
问题:pow的数值过大的时候会超过double的有效数字表示能力。很多时候pow(10,5)就会溢出了。
思路2 利用字符串相关函数处理
思路实现
思路2这个思路比较清奇,是我随便想的。
- 思路来源:字符串可以做截断;
- 思路简述:
int(str(float(vv)),10),就是利用sprintf的功能先转成str,然后取str的那几位再int向下取整。
照旧是让GPT写的,提问过程就不截图了,具体代码如下:
#include <stdio.h>
#include <stdlib.h>double roundToNDecimalPlaces(double num, int n) {char format[20];sprintf(format, "%%.%df", n); // 构造格式字符串,保留n位小数char str[50];sprintf(str, format, num); // 将浮点数转换为字符串return atof(str); // 将字符串转换回浮点数
}int main() {double num = 9.99999999;int n = 3;double result = roundToNDecimalPlaces(num, n);printf("Result: %.3f\n", result);return 0;
}
运行结果就是Result: 10.000。
思路优势和问题
优势:能充分利用现有的计算机制,并且能够达到任意高的存储精度要求。
缺点:有的实现里面可能无法调用sprintf这个函数,并且sprintf这个函数运算速度不是很快。
思路3 利用float降低精度
思路实现
思路3是脱胎于思路1的。
- 思路核心:float的精度比double低
- 思路简述:
int(float(val))。就是先把double类型的val数据强制转换为float给它丢失一下精度,然后再转int。这个实现思路只能保证float这么大的精度大小。
实现代码:
#include <stdio.h>int roundToFloat(double num) {return (int)(float)num;
}int main() {double num = 9.9999999;float temp = (float)num;int result = roundToFloat(num);printf("Temp: %f, Result: %d\n", temp, result);return 0;
}
运行结果:Temp: 10.000000, Result: 10。
思路优势和问题
优势:算得超级快。
问题:只能满足float这种精度要求。


)


目标跟踪中参数估计(似然、贝叶斯估计)理论知识)


用Java 8 stream 快速实现)

的季节性沉降、活动层厚度 (ALT)、垂直土壤水分剖面数据)








