红黑树剖析

一. 红黑树的概念

二. 红黑树的性质

三. 红黑树节点的定义

四. 红黑树的插入操作

4.1 uncle存在且颜色为红

4.2 uncle不存在或者uncle存在且为黑

五. 整体代码展示

一. 红黑树的概念

红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。

二. 红黑树的性质

（1）每个节点是黑色和红色中的一种

（2）根节点是黑色的

（3）红节点的子节点必须是黑节点（不能出现两个连续的红节点）

（4）对于一个节点，左子树内的黑色节点数目等于右子树内黑色节点数目

那我们来想想，为什么之前概念说没有一条路径会超过其他路径的两倍（即最长路径中节点个数不会超过最短路径节点个数的两倍）？

因为我们可以看见最短的路径是这条路径上所有节点都为黑色节点的时候：

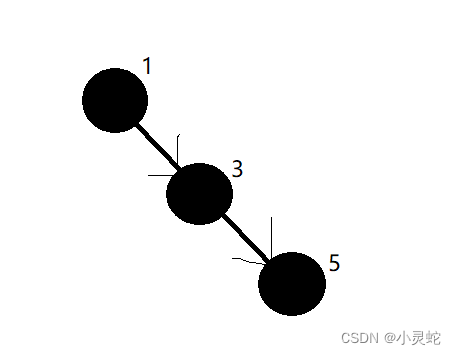
而最长路径就是一黑一红依次排列的时候：

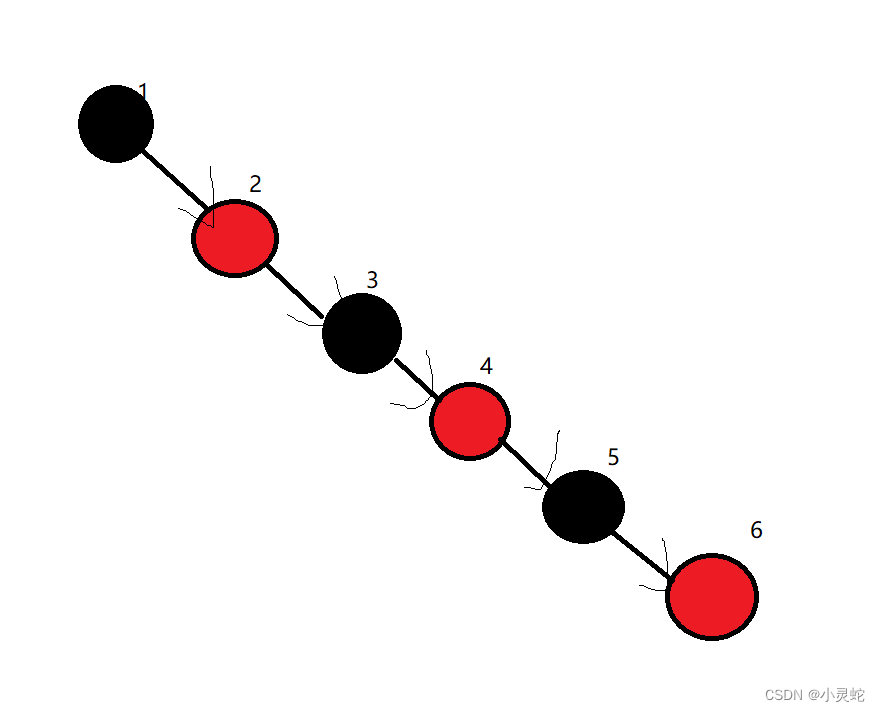
可以看见最长路径最大就为最短路径的两倍，所以最长路径是不会超过最短路径的两倍的。

三. 红黑树节点的定义

enum Colour
{RED,BLACK
};
template<class K,class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K,V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED){}
};

我们可以看见，创建新节点时，我们默认给的颜色是红色，为什么呢？

那是因为如果我们给的是黑色，就会导致左右子树的黑色节点数目不相等，与红黑树的性质相违背。

四. 红黑树的插入操作

由于红黑树除了插入操作以外，其余操作与搜索二叉树类似，所以这里讲插入操作。

那我们插入红色节点之后，是否对树的结构造成了破坏呢？

可以看见，如果父亲节点是黑色的，那实际上是不会破坏结构的，而如果父亲节点是红色，就违背了性质三（不能有连续的两个红色节点），这时候就要调节树的结构。

父亲节点为红色时，就要调节树的结构，我们先对节点起个名字。

约定：cur为当前节点，p为父节点，g为祖父节点，u为叔叔节点

4.1 uncle存在且颜色为红

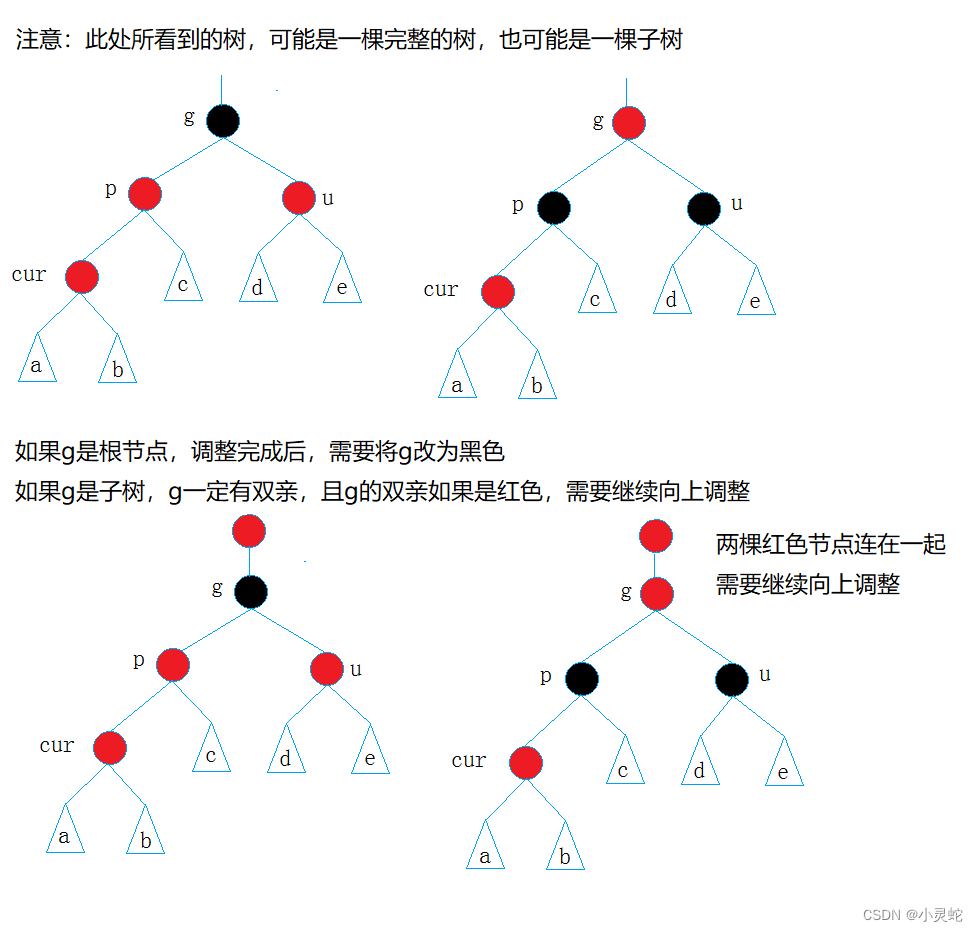
代码展示（由于parent和uncle是grandparent的左还是右不影响结果，所以这里让parent为左，uncle为右）：

Node* grandparent = parent->_parent;
Node* uncle = nullptr;
if (uncle && uncle->_col == RED)
{parent->_col = BLACK;uncle->_col = BLACK;grandparent->_col = RED;if (grandparent == _root){grandparent->_col = BLACK;}else{cur = grandparent;parent = cur->_parent;//迭代上去}
}

总结：当uncle存在且为红时，我们需要把parent和uncle变为黑色，grandparent变为红色，如果grandparent为根节点，则再次把他的颜色变为黑色，如果不是，则令cur=grandparent，迭代上去直到根节点。

4.2 uncle不存在或者uncle存在且为黑

代码展示（同上parent为左，uncle为右，这里要分cur是parent的左还是右）：

else
{//		g//	p		u//cif (cur == parent->_left){RotaleR(grandparent);parent->_col = BLACK;grandparent->_col = RED;}//		g//	p		u//		celse{RotaleL(parent);RotaleR(grandparent);cur->_col = BLACK;grandparent->_col = RED;}break;
}void RotaleL(Node* parent)
{rotalSize++;Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;if (subRL){subRL->_parent = parent;}Node* ppnode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (parent == ppnode->_left){ppnode->_left = subR;}else if (parent == ppnode->_right){ppnode->_right = subR;}subR->_parent = ppnode;}
}
void RotaleR(Node* parent)
{rotalSize++;Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;subL->_right = parent;if (subLR){subLR->_parent = parent;}Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else if (ppnode->_right == parent){ppnode->_right = subL;}subL->_parent = ppnode;}
}

总结：对于cur是parent左节点的情况，需要将这棵树在grandparent右旋，并将grandparent的颜色变为红色，parent的颜色变为黑色；对于cur是parent右节点的情况，单一的旋转不能满足条件了，此时需要先将这棵树在parent左旋，再在grandparent处右旋，并将grandparent的颜色变为红色，cur的颜色变为黑色。

五. 整体代码展示

enum Colour
{RED,BLACK
};
template<class K,class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K,V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED){}
};
template<class K,class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandparent = parent->_parent;Node* uncle = nullptr;//parent和uncle是grandparent的左还是右不影响结果//cur是parent的左还是右不影响结果if (parent == grandparent->_left){uncle = grandparent->_right;//uncle存在且为红if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandparent->_col = RED;if (grandparent == _root){grandparent->_col = BLACK;}else{cur = grandparent;parent = cur->_parent;}}else{//		g//	p		u//cif (cur == parent->_left){RotaleR(grandparent);parent->_col = BLACK;grandparent->_col = RED;}//		g//	p		u//		celse{RotaleL(parent);RotaleR(grandparent);cur->_col = BLACK;grandparent->_col = RED;}break;}}else{uncle = grandparent->_left;if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandparent->_col = RED;if (grandparent == _root){grandparent->_col = BLACK;}else{cur = grandparent;parent = cur->_parent;}}else{//		g//	u		p//				cif (cur == parent->_right){RotaleL(grandparent);parent->_col = BLACK;grandparent->_col = RED;}//		g//	u		p//		celse{RotaleR(parent);RotaleL(grandparent);cur->_col = BLACK;grandparent->_col = RED;}break;}}}return true;}void RotaleL(Node* parent){rotalSize++;Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;if (subRL){subRL->_parent = parent;}Node* ppnode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (parent == ppnode->_left){ppnode->_left = subR;}else if (parent == ppnode->_right){ppnode->_right = subR;}subR->_parent = ppnode;}}void RotaleR(Node* parent){rotalSize++;Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;subL->_right = parent;if (subLR){subLR->_parent = parent;}Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else if (ppnode->_right == parent){ppnode->_right = subL;}subL->_parent = ppnode;}}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << endl;_InOrder(root->_right);}void InOrder(){_InOrder(_root);}bool _check(Node* root,int blackNum,int refBlackNum){if (root == nullptr){if (blackNum != refBlackNum){cout <<"黑色节点数目不同" << endl;return false;}//cout << blackNum << endl;return true;}else if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "存在连续的红色节点" << endl;return false;}if (root->_col == BLACK){blackNum++;}return _check(root->_left,blackNum,refBlackNum) && _check(root->_right, blackNum,refBlackNum);}bool IsBalance(){if (_root && _root->_col == RED){return false;}int refBlackNum = 0;Node* cur = _root;while (cur){if(cur->_col==BLACK)refBlackNum++;cur = cur->_left;}return _check(_root,0,refBlackNum);}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return NULL;}
private:Node* _root=nullptr;size_t rotalSize=0;
};

总结

好了，到这里今天的知识就讲完了，大家有错误一点要在评论指出，我怕我一人搁这瞎bb，没人告诉我错误就寄了。

祝大家越来越好，不用关注我（疯狂暗示）