1 B树大家庭
有一种称为 B 树的特定数据结构,人们还使用该术语来泛指一类平衡树数据结构:
- B-Tree (1971)
- B+Tree (1973)
- B*Tree (1977?)
- B link-Tree (1981)
- Bε-Tree (2003)
- Bw-Tree (2013)
2 B+树
B+Tree 是一种自平衡【self-balance】、有序【ordered】的树数据结构,允许在 O(log n) 内进行搜索【search】、顺序访问【sequential access】、插入【insertion】和删除【deletion】。
- 它是二叉搜索树的推广,因为一个节点可以有两个以上的子节点,这样做的好处是我们可以通过串行 IO 来最小化随机 IO
- 针对读取和写入大数据块的系统进行了优化。
B+Tree 是一种 M 路搜索树,具有以下属性:
- 它是完美平衡的(即每个叶节点在树中都处于相同的深度)
- 除根节点之外的每个节点都至少是半满的,即: M/2-1 ≤ keys ≤ M-1
- 每个具有 k 个键的内部节点都有 k+1 个非空子节点
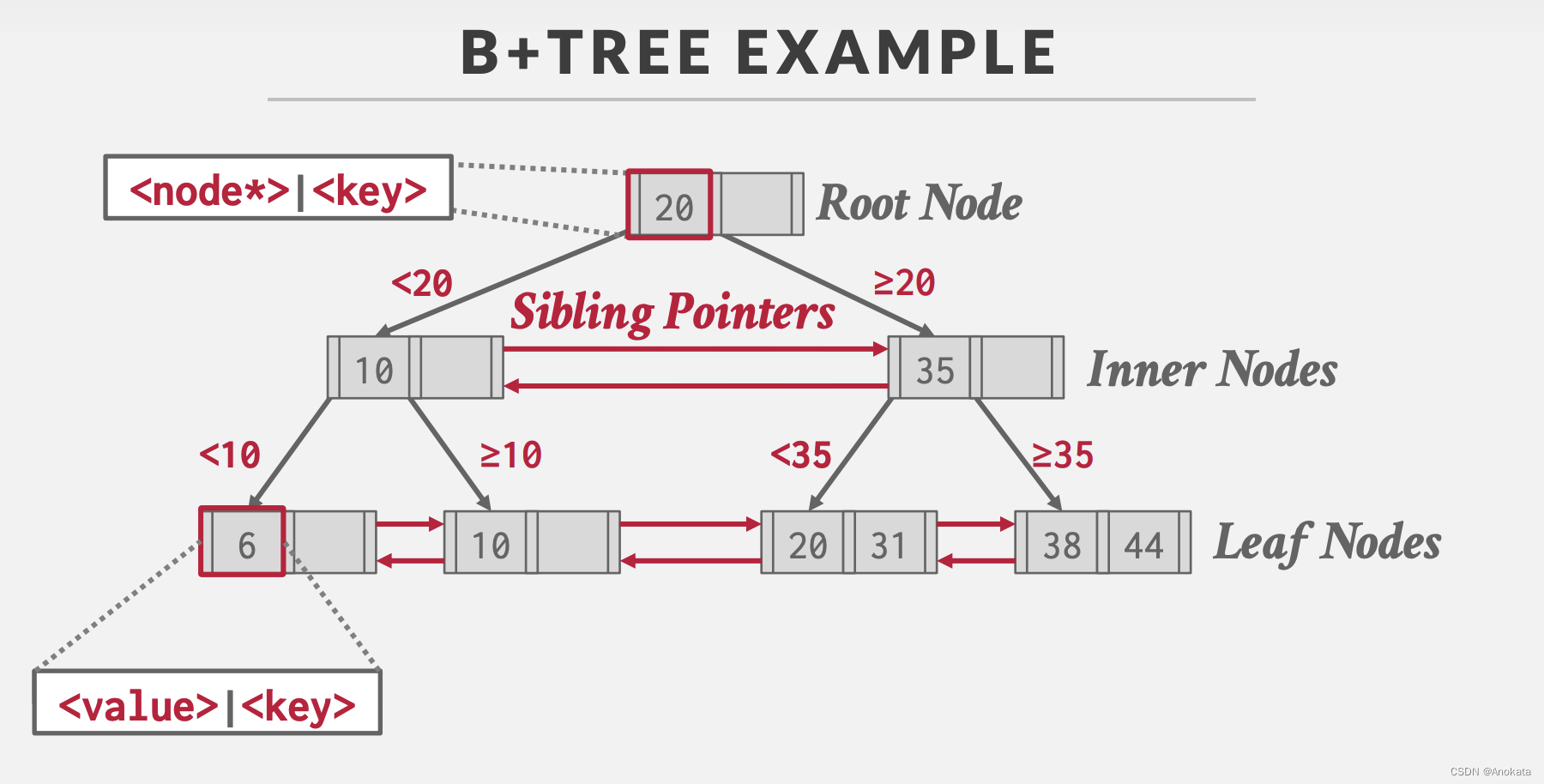
- 在一个根节点内部,我们会有这种交替的模式,一个指向另一个节点的指针,然后是一个键,再然后是一个指向另一个节点指针.....
- 在叶节点中,会有我们试图为给定键存储的值,当然这个各个系统都不一定相同
2.1 Node
每个 B+Tree 节点都由键/值对的数组组成,而该数组(通常)基于键有序,并将所有 NULL 键存储在第一个或最后一个叶节点中。
- 键【key】源自索引【index】所基于的属性【attribute(s)】
- 根据节点被分类为内部节点还是叶节点,里面的值会有所不同,如果是内部节点,那么它的值是指向其他页面的指针,而如果该节点是叶节点,则它的值是指向元组的指针(这里我不说内存地址,因为它可能不在内存中)【Record ID】(或者直接保存元组数据)。
PS : 在上图中,我们可以看到,我们有兄弟指针,也有向下的指针,但是就是没有向上的指针。这是当我们开始在这些节点上取锁存器时,我们不想让一个线程从上往下取另一个线程从下往上取,因为那样会造成死锁。兄弟阵阵也有这个问题,但是在下一讲中会给出解决办法。
2.2 B+树 Leaf Node
第一种叶节点中,key和value前后相依,而最左最右分别指向前后节点的 Page ID

第二种叶节点中,key和value分开存储,并保证有序,同时会维护一些其他原数据,比如层级【level】,以及插槽数【slots】,这对于恢复【Recover】也很有用。
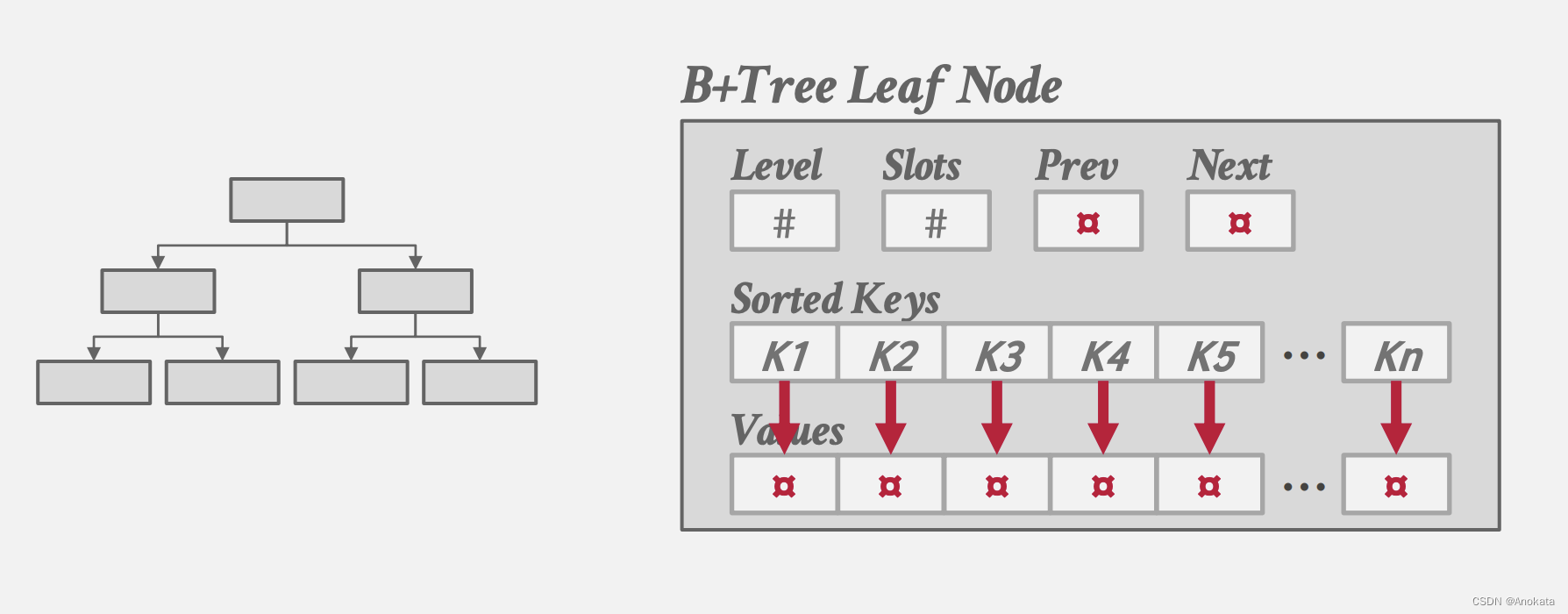
基于上面两张图,我们重点关注叶节点中的值【value】存储的方法:
- 方法1:值中存储的是记录 ID【Record ID】:叶节点中的值是指向索引条目对应的元组所在内存位置的指针
- 方法2:值中存储的是元组的真实数据(MySQL使用的方法)
- 这也被称为索引组织存储【Index-Organized Storage】
- 在叶节点存储元组的实际内容
- 而二级索引必须将记录 ID 【Record ID】存储为其值。
【注】Record ID 是Page ID 与偏移量(或者说是插槽 ID)的组合
2.3 B树 V S . B+树
原始 B 树将键和值存储在树中的所有节点中,这样做更节省空间,因为每个键仅在树中出现一次。
而B+树仅在叶节点中存储值。 内部节点仅指导搜索过程。
这样的好处是,当我们进行顺序扫描查询时,B树必须做一些向上向下的遍历,这期间也会涉及节点锁存器【latch】的操作。而对于B+树,我们只需要根据导航找打页节点,就可以顺序扫描,而无序关注父节点上的锁存器【latch】操作,这样可以带来更好的并发性,并且串行IO要比随机IO快得多。
2.4 B+树插入
- 找到正确的叶节点
- 按键顺序将数据条目插入到 L 中
- 如果 L 有足够的空间,完成!
- 否则,将 L 中的 keys 拆分为 L 和一个新节点 L2
- 均匀的重新分配键,并将中值插入到父节点中
- 将指向 L2 的索引项插入到 L 的父节点中
PS 要分割内部节点,请均匀地重新分配条目,但要将中间键上推到父节点。
动画链接:B+ Tree Visualization
2.5 B+树删除
- 从根节点开始,找到条目所属的叶节点 L
- 删除条目
- 如果 L 至少时半满,完成!
- 如果L只有 M/2-1 个条目
- 场景进行重新分配,从兄弟节点上借值
- 如果重新分配失败,则将 L 和同级的兄弟节点进行合并,需要注意的是,当发生合并时,必须删除 L 父节点中指向 L 或者与其合并的兄弟节点的条目【entry】
2.6 选择条件
在哈希表中,我们唯一可以做的操作,就是哈希键【hash key】等于【=】我要找的 key.。我们没有办法做诸如小于大于的操作,甚至不可以做部分 key 查询,我们必须查询完整的key,比如当我们有一个ABC三列的索引,我们没办法查询只有AB列的key。
对于哈希索引,我们的搜索键【search key】中必须有所有属性【attributes】。
而对于B+树索引,我们必须要求搜索【search key】中必须有所有属性【attributes】,它可以只包含部分属性。
示例:<a,b,c> 上的索引
- 支持 (a=1 AND b=2 AND c=3)
- 支持(a=1 AND b=2)
- 支持 (b=2), (c=3)
但是,并非所有 DBMS 都支持这一点,oracle 通过跳跃扫描【skip scan】实现了第三点。
栗子:
假设我们有A和B列上的 b+ 树索引,下面进行前缀查询【Prefix Search】
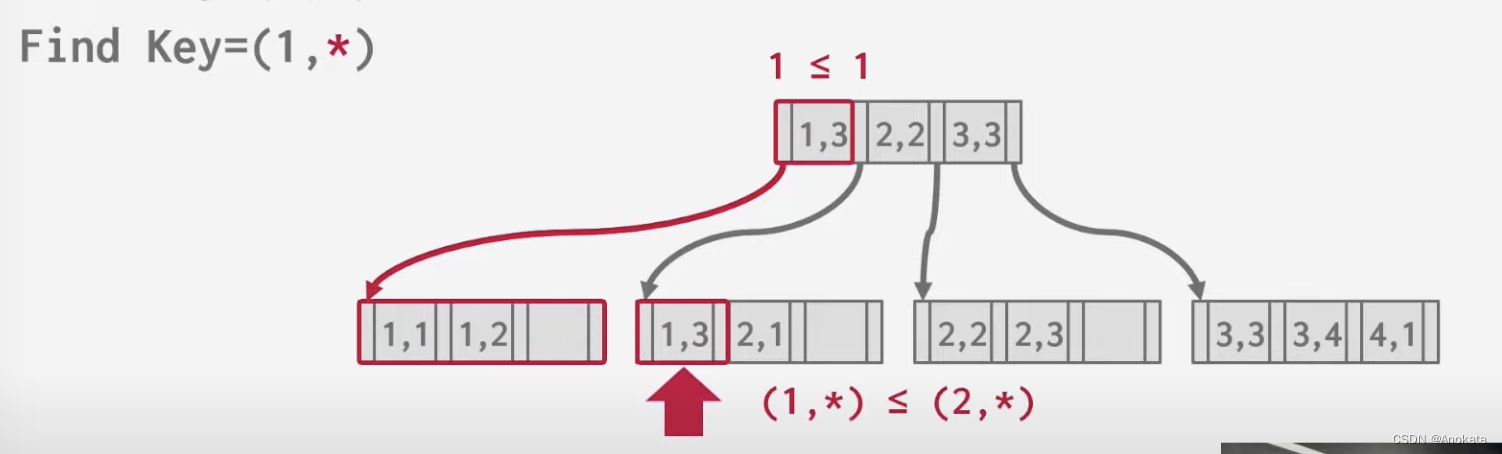
case 1 我们的查询键是(1,2)
- 在中间节点上,我们逐个比较(当然数据库系统可能更高级),在第一个元素上,我们依次检查 1 <= 1 和 2 <= 3 两个表达式,得出数据应该在左子树中的揭露
- 然后根据指针导航到左子树,就可以查得元素

case 2 我们的查询键是(1,*)
- 我们检查 1 <= 1表达式,并根据结论导航到叶节点中
- 在第一个叶节点中,现在我继续扫描,并在遇到每一个key上计算做表达式计算,直到遇到违反该表达式约束的记录时结束扫描,在栗子中就是 (1,*) <= (2,*)
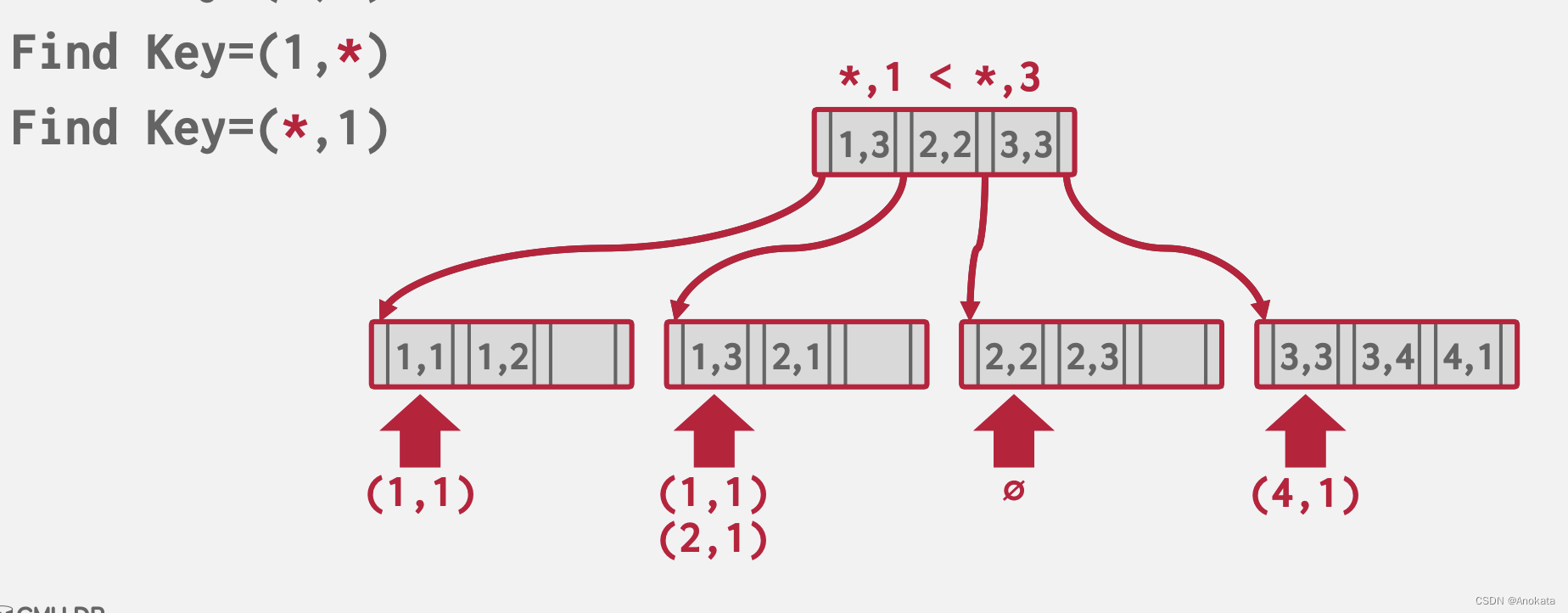
case 3 我们的查询键是(*,1)
- 我们的查询键上没有索引的第一部分,那么意味着我需要查询所有,在 oracle 中应该会利用多线程技术来对树的不同叶节点分开计算,并最终将结果组合到一起
2.6 重复键
目前有两种处理重复键的方法
- 方法 1 :Append Record ID,
- 添加元组的唯一记录 ID 【Record ID】作为键的一部分,以确保所有键都是唯一的。
- DBMS 仍然可以使用部分键【partial keys】来查找元组。
- 方法 2:Overflow Leaf Nodes
- 允许叶节点分割出一个溢出节点,并在该节点上存放重复键
- 但是维护和修改比较复杂。
Append Record ID 栗子:
1️⃣ 在如下的 B+ 树中,我们将记录 ID 【Record ID】作为键的一部分,可以看到它的组成是 key + RecordID
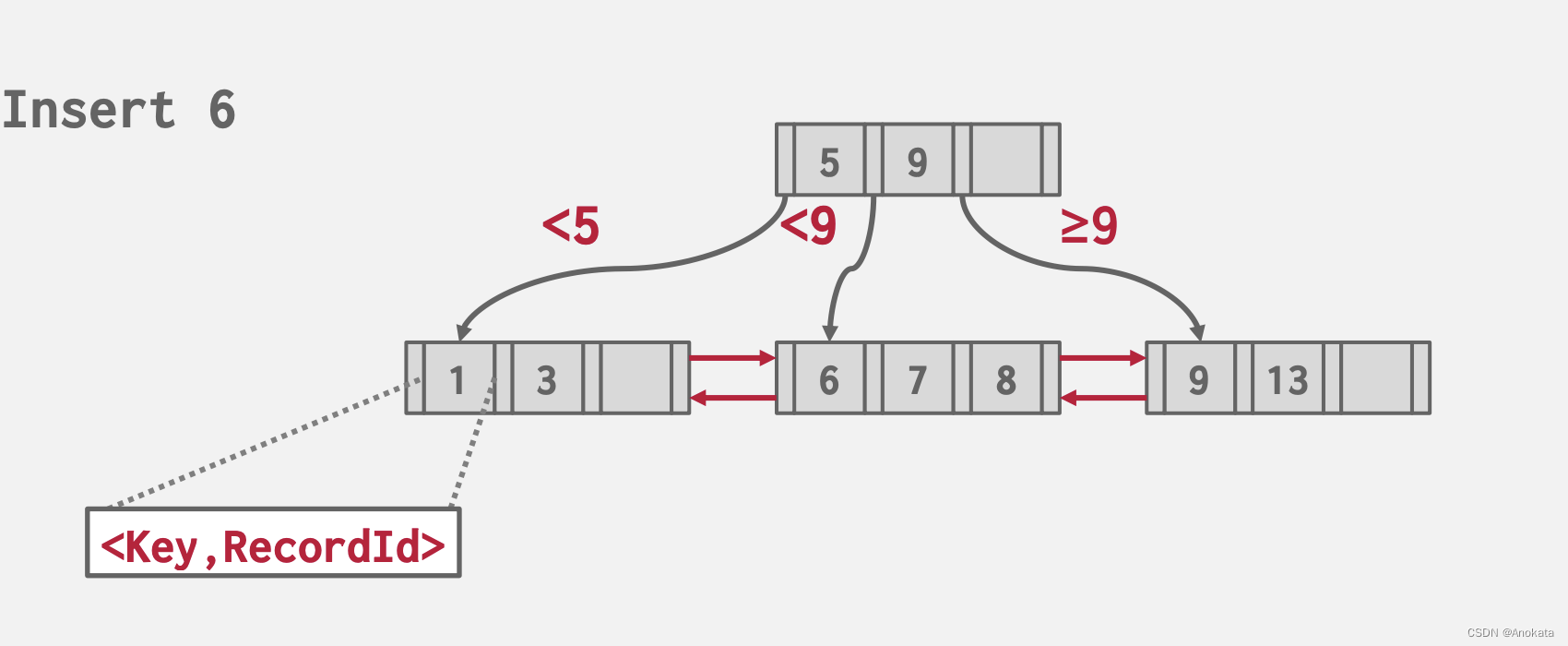
2️⃣ 此时,我们想要在此 B+ 树中插入元素 6,数据库系统会负责将插入语句转换为 :
- insert <6,(Page,SLot)>
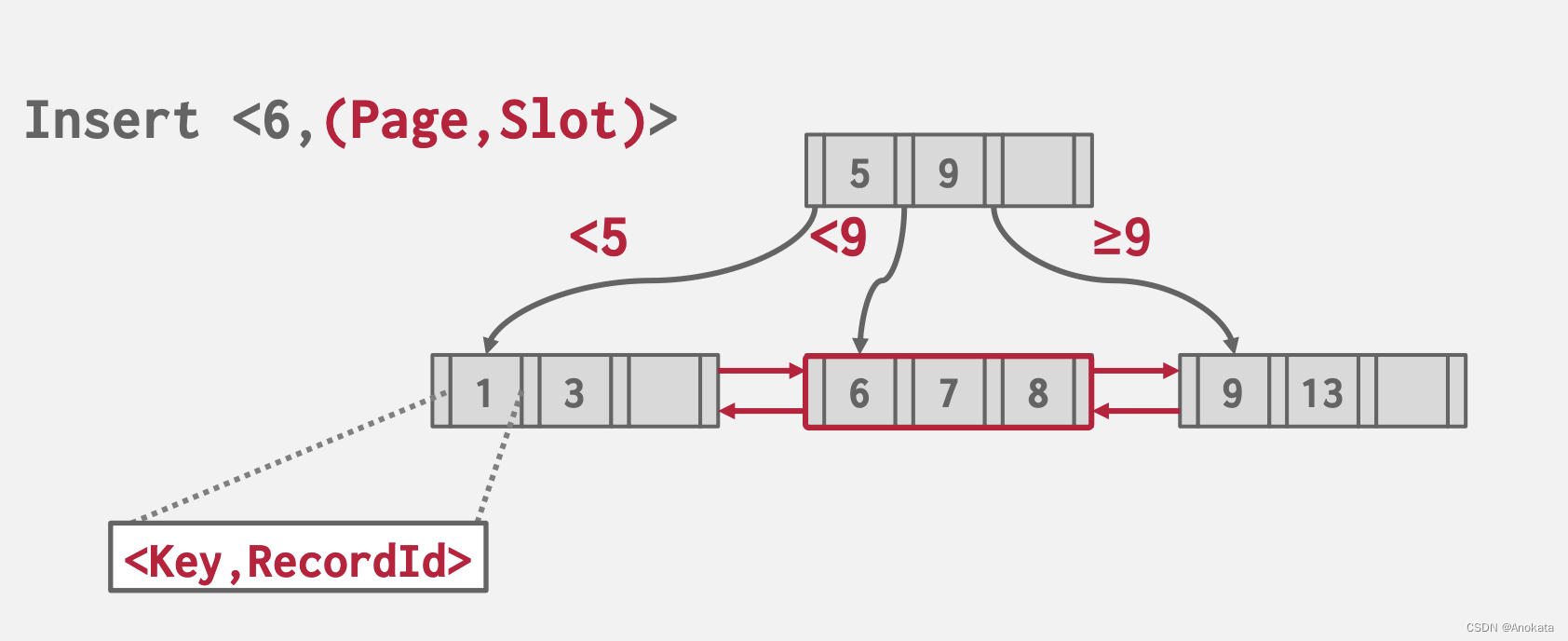
3️⃣ 而注意此时叶节点已经满了,我们将元素做拆分这样就可以插入元素 6 了。需要注意的是,如果6 所在的列上有唯一索引,那么就无需这种特殊处理了。

Overflow Leaf Nodes 栗子:
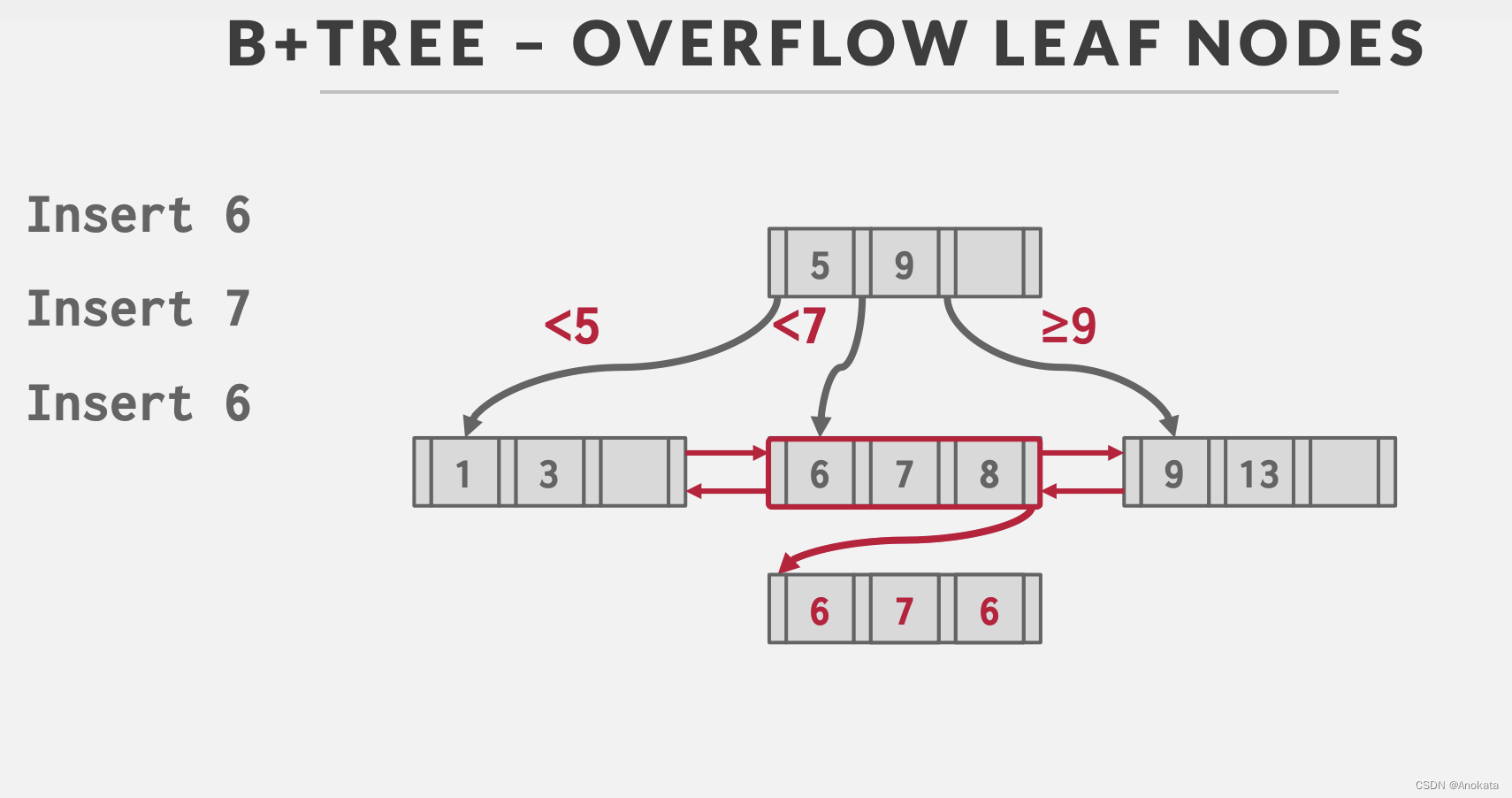
1️⃣ 同样是 插入元素 6 ,我们计算的到叶节点,而该叶节点满了,我们意识到插入元素在该叶节点中有重复记录,因此我们增设一个溢出页,并将元素插入其中。

2️⃣ 我们可以继续插入重复的元素,比如插入 7 ,

3️⃣ 再次插入 6
2.7 聚簇索引
表【table】按主键指定的排序顺序进行存储,这可以是堆组织存储【heap-organized storage】,也可以是索引组织存储【index-organized storage】。
一些 DBMS (比如MySQL)始终使用聚集索引,如果表不包含主键,DBMS 将自动创建隐藏主键。
2.8 聚簇的B+树
聚簇索引扫描
当我们进行扫描时,假设我们按索引组织存储,当我们开始扫描叶节点,来查找所有我查找的元组时,我们可以保证按照键顺序所定义的排序顺序来获得页面【page】。

遍历到最左边的节点,然后从所有叶节点中检索元组。
非聚簇索引扫描
而以元素在非聚簇索引中出现的顺序进行扫描,这样会导致很高的重复 IO 读取,从而降级性能。
更好的方法是找到查询所需的所有元组,然后根据其 Page ID 对它们进行排序,再顺序读取,这样每个页面只需要检出一次。

更多关于 B + 树的设计决策,请参考 Google 的书 Modern B-tree techniques | IEEE Conference Publication | IEEE Xplore
2.9 节点大小
在前面介绍中,我们知道页与节点是1:1大小的,但是某些数据库,比如 DB2,允许对某个表或索引,单独设置其数据库中页的大小。依赖于你所在的硬件,你可以设置不同的页大小。比如你的硬件存储越慢,那么你就应该设置更高的页大小,以减少磁盘 IO。
- HDD: ~1MB的页
- SSD: ~10KB的页
- In-Memory: ~512B的页
2.10 MERGE THRESHOLD
某些 DBMS 在节点半满时并一定会合并节点
- B+Tree节点平均占用率为69%。
延迟合并操作可以减少重组【reorganization】量。
最好只让较小的节点存在,然后定期重建整个树。
这就是为什么 PostgreSQL 将他们的 B+Tree 称为“非平衡”B+Tree (nbtree)。
2.11 可变长的键【variable-length key】
方法1:指针,即实际上我们并不会将键本身存在节点中,而是只需存储一个到它的指针,但是这会带来随机 IO。
- 将键存储为指向元组属性的指针。
- 也称为 T 树(内存 DBMS)
方法:可变长度节点【Variable-Length Nodes】,目前为止只有一些学术数据库才使用这种方案
- 索引中每个节点的大小可能会有所不同
- 因此需要仔细的内存管理
方法3:填充【Padding】
- 始终将键填充到键类型的最大长度。
方法4:键映射/间接【Key Map / Indirection】,与页内的可变长处理方案一样,详见 slotted page
- 嵌入一个指向节点内键+值列表的指针数组
2.12 节点内搜索【intra-node search】
一旦我们进入到某个节点,我们首先将其放入内存,然后在其中查找键,以决策我们是导航到哪个子节点上。
那么节点内搜索的方案有哪些?
方法1:线性
- 一种比较粗犷的方法是从头到尾扫描节点键。
- 另一种比较好点的方法是使用 SIMD(它是 CPU 提供的一类高级指令,基本上是它有一个向量指寄存器,我们可以放入多个数据,然后可以通过一个命令进行比较)【SIngle Instruction Multi Data】进行矢量化比较。
栗子:
1️⃣ 顺序扫描

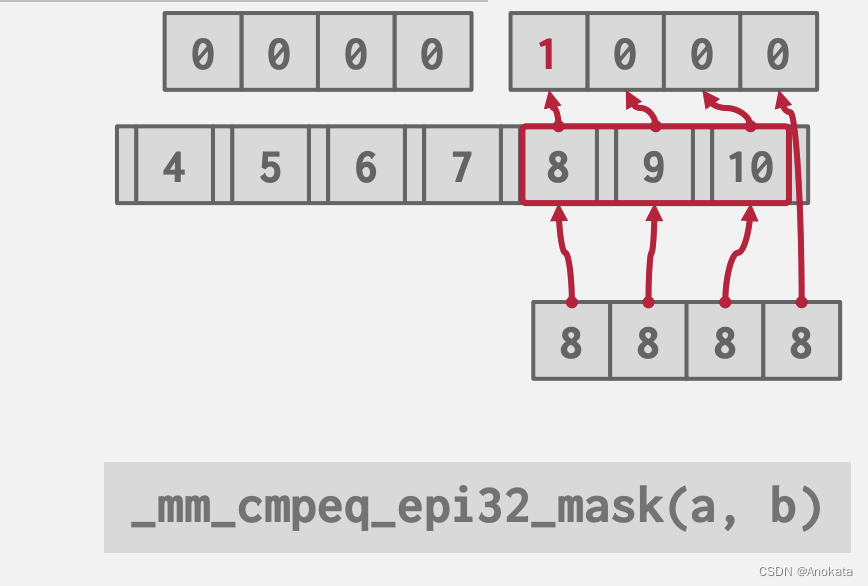
2️⃣ 与其逐个比较,我们可以利用 SIMD,并行的与 8 进行比较运算,得到最终的输出结果:
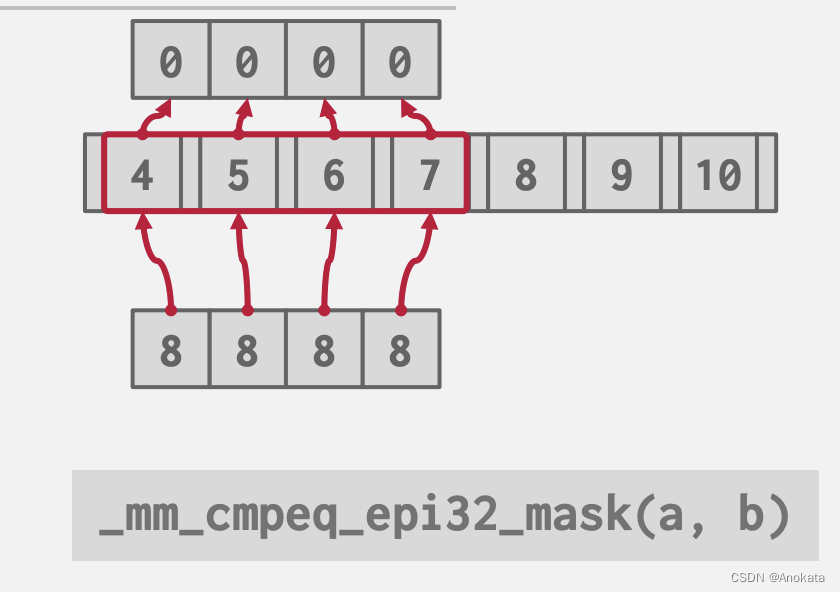
当没有匹配的键时,我们可以继续向下计算,这次就有了匹配项。SIMD 时高效的,但是它仍然时线性的,只不过是批量的。
方法 2 :如果键是有序的,我们可以使用二分查找
- 跳转到中间键,根据比较结果决策向左/向右旋转。
方法 3 :插值【Interpolation】,当你知道你的键没有间隙时,且总是单调增/减的,我么可以通过简单的数学计算出对应键的位置。
- 根据已知的键分布,确定所需键的大致位置。
2.13 其他优化
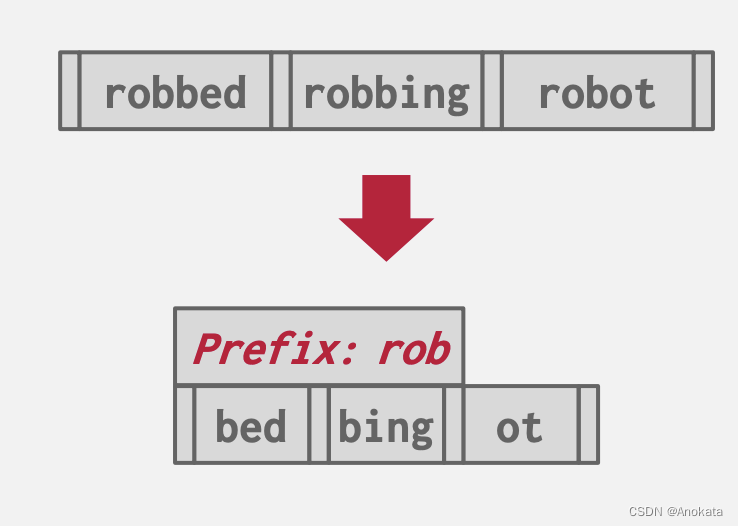
前缀压缩
同一叶节点中的有序键可能具有相同的前缀。
与其每次都存储整个键,而不如提取公共前缀并仅存储每个键的唯一后缀。
- 许多变体
去重复【D E D U P L I C AT I O N】
非唯一索引最终可能会在叶节点中存储同一键的多个副本。
叶节点可以只存储键一次,然后维护具有该键的元组的“倒排列表【posting list】”(类似于我们讨论的哈希表)。

后缀截断【Suffix Truncation】
首先,我们知道内部节点中的键仅用于“引导流量”,因此我们可能不需要存储整个完整的键,而只需要存储将探测正确路由到索引所需的最小前缀即可】。
1️⃣ 之前

2️⃣ 之后

指针旋转【POINTER SWIZZLING】
节点使用 Page ID 来引用索引树中的其他节点。
DBMS 在遍历期间必须从页表中获取内存位置。
如果页面始终固定【Pin】在缓冲池中,那么我们可以存储原始指针而不是页面 ID。 这避免了从页表中查找地址
栗子:
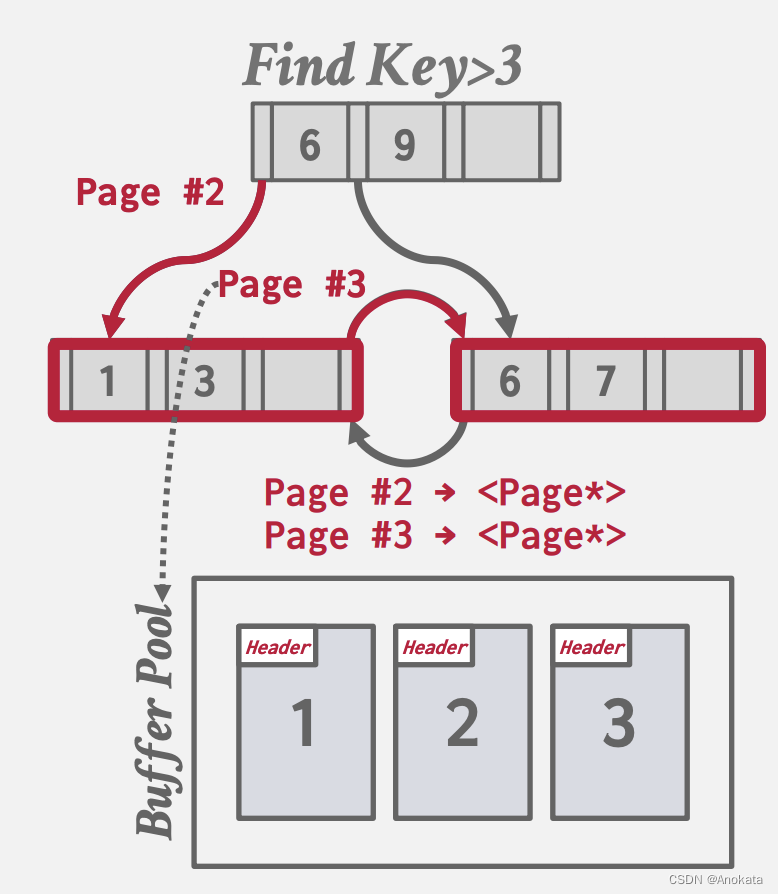
1️⃣ 当我们查找大于 3 的元素时,我们与 6 比较,得出应该导航到左子节点,假设其 Page ID = 2,那么我们请求 Buffer Pool 给予我 Page ID = 2的页面的指针(内存地址)。

2️⃣ 接来下我们可能需要查询其兄弟节点,即 Page ID = 3,我们又需要回到 BufferPool 请求指针。
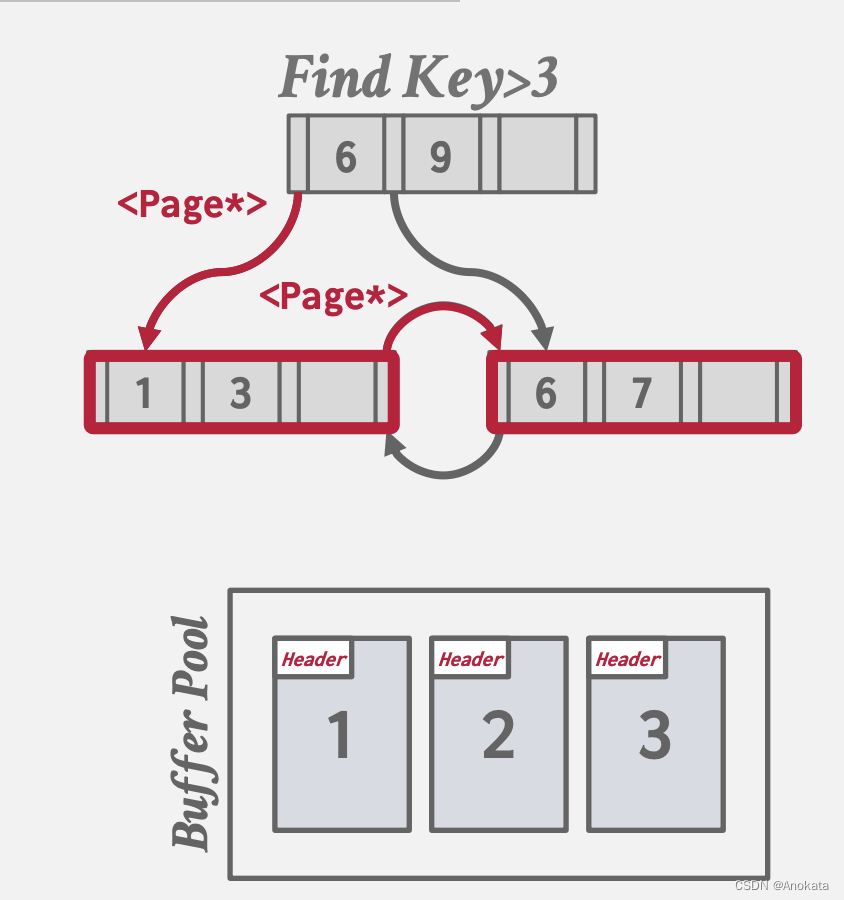
3️⃣ 假设我们将页固定在内存中,不会被驱逐,那么我们可以直接替换树中的 Page ID 为真实内存指针,这样必须每次都要去页表中换取对应内存指针了。
批量插入【Bulk insert】
为现有表构建新的 B+Tree 的最快方法是首先对键进行排序,然后从下往上构建索引。 这个在 MySQL 官方文档中叫 Sorted Index Builds。
- 第一阶段,扫描聚簇索引,并生成新建索引的索引条【index entries】,并将其写入 sort buffer ,当 sort buffer 满了时,里面的条目会被排序,并写入临时中间文件,这个过程也被称为 RUN
- 在第二阶段,在一次或多次 RUN 写入临时中间文件后,对文件中的所有条目执行归并排序。
- 在第三个也是最后一个阶段,排序后的条目被插入到 B 树中; 最后阶段是多线程的。
在最后一个阶段中,索引条目可以是一条条插入的,但是这样速度也太慢了。此方法涉及打开 B 树游标以查找插入位置,然后使用乐观插入将条目插入到 B 树页面中。 如果由于页面已满而导致插入失败,则将执行悲观插入,这涉及打开 B 树游标并根据需要拆分【spli】和合并【merge】 B 树节点以为条目找到空间。 这种“自上而下”建立索引的方法的缺点是搜索插入位置的成本以及B树节点的不断分裂和合并。
排序索引构建【Sorted Index Build】使用“自下而上”的方法来构建索引。

写优化的b树【WRITE-OPTIMIZED B+ TREE】
当 DBMS 必须拆分/合并节点时,修改 B+ 树的成本很高。
- 最坏的情况是 DBMS 重新组织整个树。
- 导致产生拆分/合并的工作者【工作负载】负责完成该工作。
如果有一种方法可以延迟更新,然后批量应用多个更改,该怎么办?
解决方法:不是立即应用更新,而是将对键/值条目的更改存储在内部节点的日志缓冲区中。简而言之,每一个 root 节点和 inner 节点,会派生出一个 mod log,我们的更新不会立即传播到叶节点,我们会违反 b+ 树的约束,即叶节点是真正的值所在的地方,而是可以将条目【entry】插入到 mod log 中。
- 也称为 Bε 树
当缓冲区已满时,更新会逐步级联到较低的节点。
栗子:
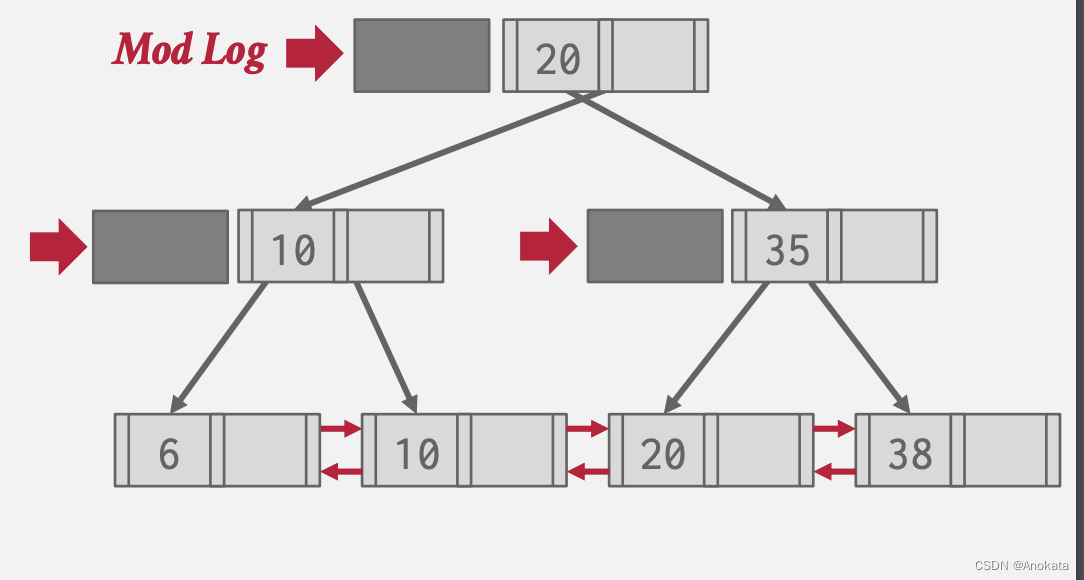
1️⃣ 我们现在想插入元素7,我们没有详细查找节点,而是直接将其写入到跟节点的 mod log 中
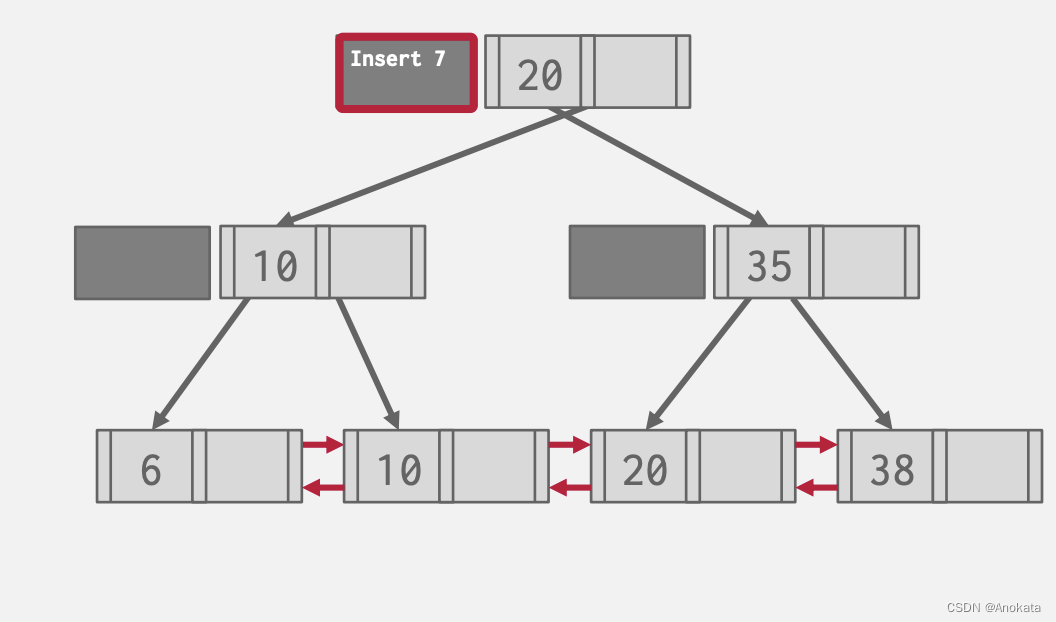
2️⃣ 然后我们想删除10
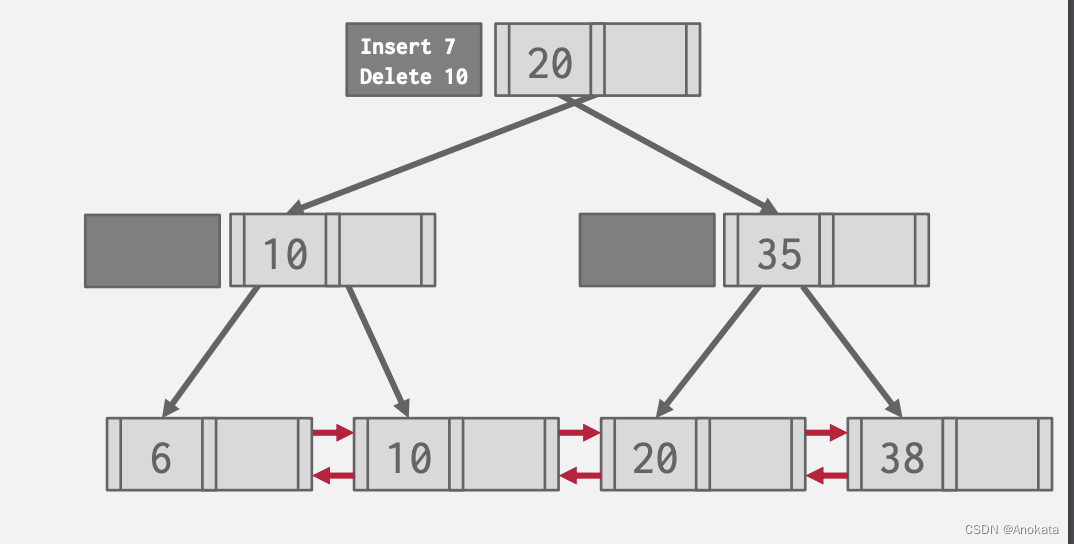
3️⃣ 现在我们想查找元素10,我们会先搜索下 mod log ,在其中我们发现元素 10 被删除了,那么我们页不需要向下查找了
4️⃣ 现在我们插入元素 40,根节点的 mod log 满了,我们会将日志传播到子节点中
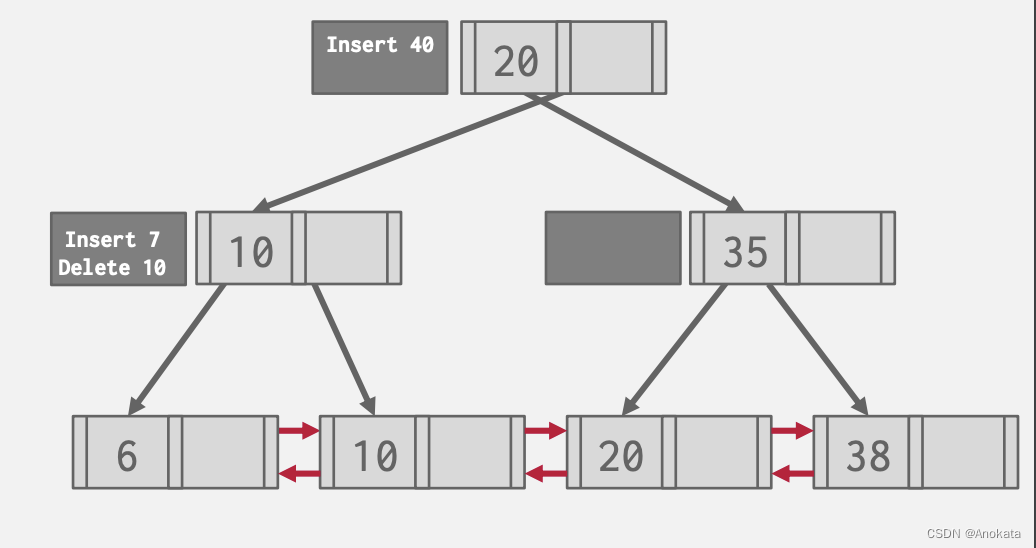



)

![每日一题 --- 四数之和[力扣][Go]](http://pic.xiahunao.cn/每日一题 --- 四数之和[力扣][Go])




)



)




