---

题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

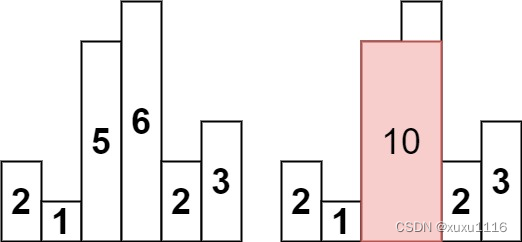
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

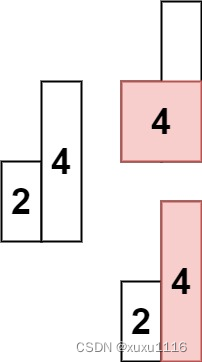
输入： heights = [2,4]
输出： 4

提示：

• 1 <= heights.length <=10⁵
• 0 <= heights[i] <= 10⁴

---

解法

我们可以枚举每根柱子的高度 h 作为矩形的高度，利用单调栈，向左右两边找第一个高度小于 h 的下标 left _i , right _i 。那么此时矩形面积为 h×(right _i − left _i −1)，求最大值即可。

时间复杂度 O(n)，空间复杂度 O(n)。其中 n 表示 heights 的长度。

方法一

class Solution(object):def largestRectangleArea(self, heights):""":type heights: List[int]:rtype: int"""n = len(heights)stk = []left = [-1] * nright = [n] * nfor i, h in enumerate(heights):while stk and heights[stk[-1]] >= h:right[stk[-1]] = istk.pop()if stk:left[i] = stk[-1]stk.append(i)return max(h * (right[i] - left[i] - 1) for i, h in enumerate(heights))

方法二

class Solution(object):def largestRectangleArea(self, heights):""":type heights: List[int]:rtype: int"""n = len(heights)stk = []left = [-1] * nright = [n] * nfor i, h in enumerate(heights):while stk and heights[stk[-1]] >= h:stk.pop()if stk:left[i] = stk[-1]stk.append(i)stk = []for i in range(n - 1, -1, -1):h = heights[i]while stk and heights[stk[-1]] >= h:stk.pop()if stk:right[i] = stk[-1]stk.append(i)return max(h * (right[i] - left[i] - 1) for i, h in enumerate(heights))

---

运行结果

方法一

方法二