【智能算法】天鹰优化算法（AO）原理及实现

在这里插入图片描述

1.背景

2021年，L Abualigah等人受到天鹰猎食过程启发，提出了天鹰优化算法（Aquila Optimizer，AO）。

2.算法原理

2.1算法思想

AO模拟天鹰 4 种不同的捕食策略建立数学模型，根据搜索空间内解的不同特性，灵活应用不同的搜索策略。

2.2算法过程

扩展探索阶段：

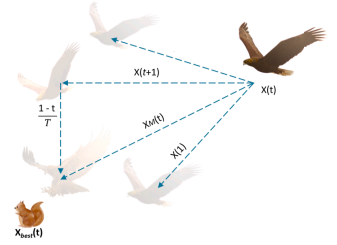
在第 1 个阶段，天鹰通过垂直俯身的高空翱翔搜索猎物并选择搜索区域:
$X_{1}\left(t+1\right)=X_{\mathrm{best}}\left(t\right)\times\left(1-\frac{t}{T}\right)+\left(X_{\mathrm{M}}\left(t\right)-X_{\mathrm{best}}\left(t\right)\times\mathrm{rand}\right).\\\\X_{\mathrm{M}}\left(t\right)=\frac{1}{N}\sum_{i=1}^{N}X_{i}\left(t\right).\tag{1}$
在这里插入图片描述

缩小探索阶段：

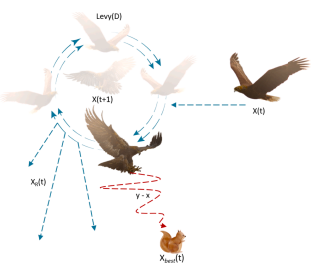
模拟天鹰短滑翔攻击行为：
$X_{2}\left(t+1\right)=X_{\mathrm{best}}\left(t\right)\times\mathrm{Levy}\left(D\right)+X_{\mathrm{R}}\left(t\right)+\left(y-x\right)\times\mathrm{rand}\times1.\tag{2}$
x,y代表螺旋飞行：
$rcos(\theta)\\x=rsin(\theta) \\ r = r1+UD_1\\ \theta = -\omega D_1+3\pi/2\tag{3}$
在这里插入图片描述

扩大开发阶段：

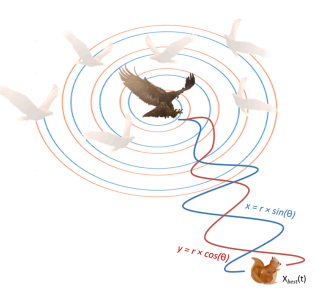
模拟天鹰的低空慢降攻击：
$\begin{gathered} \boldsymbol{X}_{3}(t+1) =\alpha\left(\boldsymbol{X}_{\mathrm{best}}\left(t\right)-\boldsymbol{X}_{\mathrm{M}}\left(t\right)\right)-\mathrm{rand}\times\mathbf{1}+ \delta((U-L)\times\mathrm{rand}+L)\times\mathbf{1}. \end{gathered}\tag{4}$
在这里插入图片描述

缩小开发阶段：

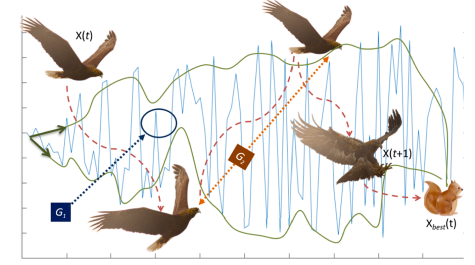
模拟天鹰行走及狩猎地面上移速较慢的生物：
$\begin{array}{c}{X_{4}\left(t+1\right)=Q_{\mathrm{F}}\times X_{\mathrm{best}}\left(t\right)-G_{1}\times\bar{X}\left(t\right)\times\mathrm{rand}-}{G_{2}\times\mathrm{Levy}\left(D\right)\times\mathbf{1}+\mathrm{rand}\times G_{1}\times\mathbf{1}.}\\\end{array}\tag{5}$
其中，参数表述为：
$Q_{\mathrm{F}}(t)=t^{(2\times\mathrm{mnd}-1)/(1-T)^{2}}.\\ G_{1}=2\times\mathrm{rand}=1.\\ G_{2}=2\times(1-t/T).\tag{6}$
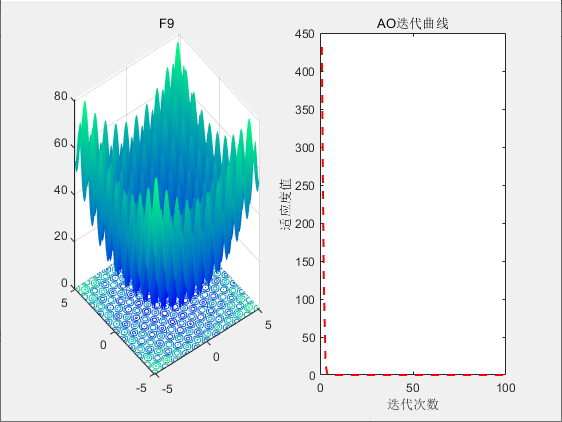
在这里插入图片描述

伪代码：
在这里插入图片描述

3.结果展示

在这里插入图片描述

4.参考文献

[1] Abualigah L, Yousri D, Abd Elaziz M, et al. Aquila optimizer: a novel meta-heuristic optimization algorithm[J]. Computers & Industrial Engineering, 2021, 157: 107250.

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/782482.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！