| java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 |
|---|
文章目录
- 1. 异或运算
- 2. 全数组二分查找+异或奇偶
- 3. 偶数下标二分查找
1. 异或运算
| 解题思路:时间复杂度O( n n n),空间复杂度O( 1 1 1) |
|---|
- 利用异或操作,因为异或满足结合律和交换律
- 两个二进制位,相同的数异或结果为0,两个不同的数异或结果为1
- 而对与10进制,两个相同的数异或必然为0,因为两个10进制数,每位二进制数都相同,也就是a ^ a = 0
- 因此将数组中所有的数全部进行异或运算,出现两次的数都会为0
- 而任何数a ^ 0都等于a本身
- 因此例如aabcc这样的序列,想要找到中间那个出现次数一次的b,只需要异或即可
1、a^a = 0, 2、0^b = b, 3、b^c = b^c, 4、b ^c ^c = b^0 = b
| 代码 |
|---|
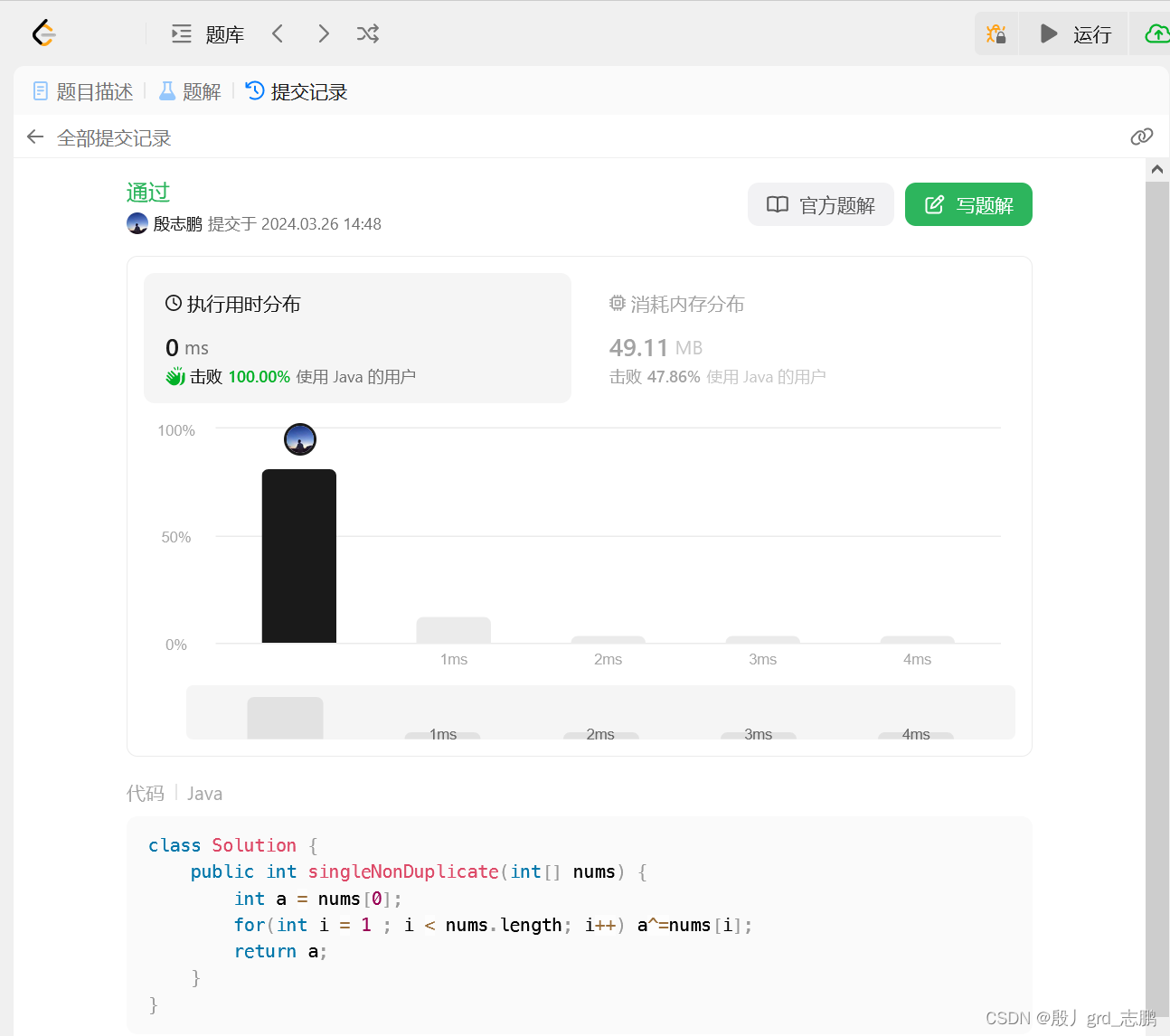
class Solution {public int singleNonDuplicate(int[] nums) {int a = nums[0];//异或操作,两个相同的数异或会归0,并且满足交换律for(int i = 1 ; i < nums.length; i++) a^=nums[i];return a;//最终所有出现两次的数会全部抵消,只剩下一个出现一次的数a}
}
2. 全数组二分查找+异或奇偶
| 解题思路:时间复杂度O( l o g 2 n log_2n log2n),空间复杂度O( 1 1 1) |
|---|
- 利用整个数组的数字分配规律,来进行二分查找
- 因为整个数组只有一个元素x的个数是奇数—1个,其余都是偶数有2个。所有以x为中心,两边都是偶数个元素。而x左边的元素会保证偶数分配规律(每个数字第一次出现都是偶数下标),而x只有一个,破坏了规律,x右边的变成符合奇数规律
- 因此可以利用这个偶数规律,x左边的元素,从偶数0开始,依次判断是否nums[y] = nums[y+1]即可,其中y是偶数
- 而x右边的元素,会被x破坏偶数关系,将会从奇数开始两个两个分布,因此x右边判断是否满足nums[z] = nums[z+1]即可,其中z是奇数
- 有了上面的原理后,我们就可以利用这个信息,
x左边的数字分配规律为,如果是偶数下标一定是第一个,如果是奇数下标一定是这个数字的第二个。- 也就是说如果mid为偶数,比较nums[mid]和nums[mid+1]. 如果是奇数比较nums[mid-1]和nums[mid]
- 如果比较结果为相等,说明满足偶数规律,也就是mid < x.mid还在x的左边,因此调整左边界
使用的异或奇偶性质参考:
| 位运算https://blog.csdn.net/grd_java/article/details/136119268 |
|---|
- 如果mid是偶数,mid +1 操作相当于 mid ^ 1
例如2是偶数,二进制为0010,异或1(二进制0001)结果为0011.
- 如果mid是奇数,mid - 1 操作相当于 mid ^ 1
例如1是奇数,二进制为0001,异或1(二进制0001)结果为0000.
| 代码 |
|---|
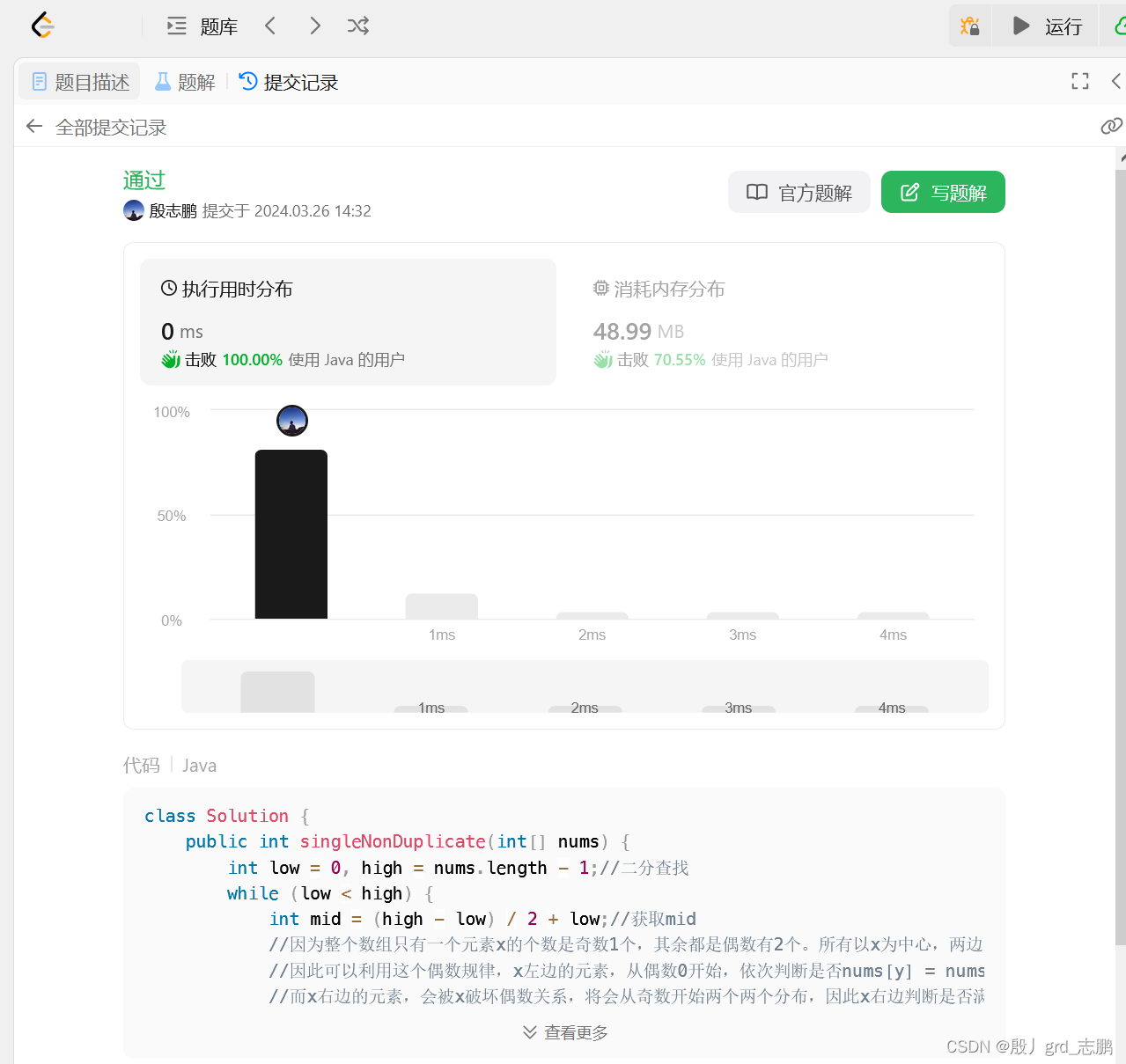
class Solution {public int singleNonDuplicate(int[] nums) {int low = 0, high = nums.length - 1;//二分查找while (low < high) {int mid = (high - low) / 2 + low;//获取mid//因为整个数组只有一个元素x的个数是奇数1个,其余都是偶数有2个。所有以x为中心,两边都是偶数个元素//因此可以利用这个偶数规律,x左边的元素,从偶数0开始,依次判断是否nums[y] = nums[y+1]即可//而x右边的元素,会被x破坏偶数关系,将会从奇数开始两个两个分布,因此x右边判断是否满足nums[z] = nums[z+1]即可//有了上面的原理后,我们就可以利用这个信息,x左边的数字分配规律为,如果是偶数下标一定是第一个,如果是奇数下标一定是这个数字的第二个。//也就是说如果mid为偶数,比较nums[mid]和nums[mid+1]. 如果是奇数比较nums[mid-1]和nums[mid]//如果比较结果为相等,说明满足偶数规律,也就是mid < x.mid还在x的左边,因此调整左边界if (nums[mid] == nums[mid ^ 1]) {//如果是偶数mid和mid+1比,奇数mid和mid-1比low = mid + 1;} else {//如果不相等,说明不满足偶数规律,也就是mid >= x,调整右边界high = mid;}}return nums[low];//最后low将指向x位置}
}
3. 偶数下标二分查找
| 解题思路:时间复杂度O( l o g 2 n log_2n log2n),空间复杂度O( 1 1 1) |
|---|
- 法二是整个数组去找。并没有完全利用偶数性质
- x虽然是打破偶数规则的数,但是其本身依然符合偶数规则(第一次出现是在偶数下标位置)
- 而x后面的元素全部因为x的影响,无法满足偶数规则
- 而且x也是第一个不满足nums[x] == nums[x+1]的数(x是偶数)。
- 因此这个问题变成了,找到第一个nums[x] != nums[x+1]的数(x是偶数)
简单来说,x是第一个满足nums[x] != numsx+1的数,那么x就是那个只出现1次的数。
其余逻辑和法二一样
如何保证所有数都是偶数?
- 如果当前数是奇数的话,让其-1。
- 如果当前数是偶数的话,让其-0.
- 通过与操作完成即可。也就是mid -= mid&1.
假设mid是偶数2,二进制为0010,2&1 = 0010 & 0001 = 0000.也就是mid&1 = 0.mid - 0 = mid。
假设mid是奇数3,二进制为0011,3&1 = 0011&0001 = 0001,也就是mid&1 = 1.mid -=mid&1 ==> mid -1
| 代码 |
|---|
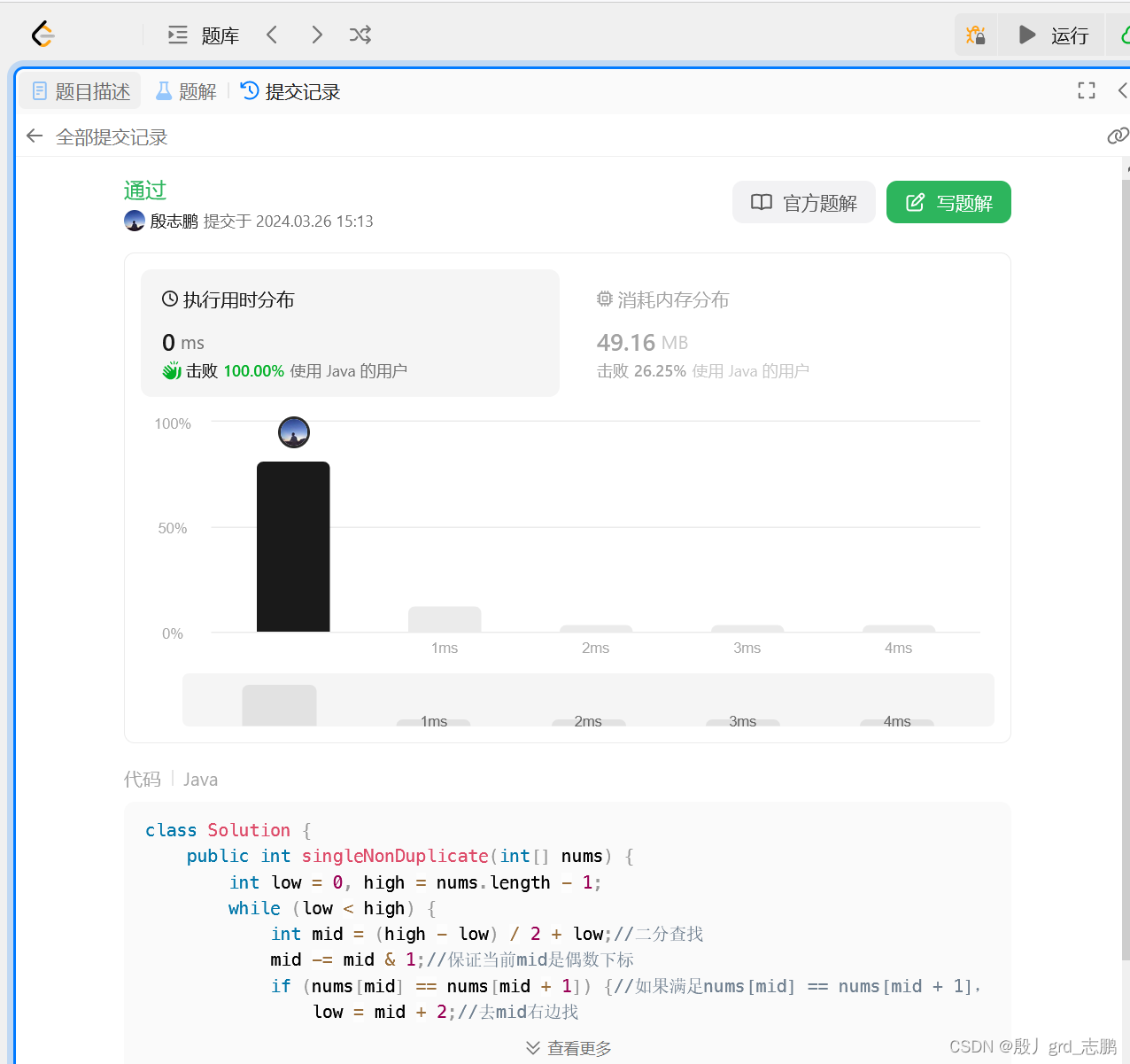
class Solution {public int singleNonDuplicate(int[] nums) {int low = 0, high = nums.length - 1;while (low < high) {int mid = (high - low) / 2 + low;//二分查找mid -= mid & 1;//保证当前mid是偶数下标if (nums[mid] == nums[mid + 1]) {//如果满足nums[mid] == nums[mid + 1],说明现在mid<xlow = mid + 2;//去mid右边找} else {//如果不满足,则mid>=x, 但是不能保证就是x,所以需要继续左边找high = mid;//去mid左边,直到找到x为止}}return nums[low];}
}







)







)

—— pod的深入理解)
![[DS]Polar靶场web(一)](http://pic.xiahunao.cn/[DS]Polar靶场web(一))
