大家好,我是苏貝,本篇博客带大家了解快速排序,如果你觉得我写的还不错的话,可以给我一个赞👍吗,感谢❤️
目录
- 一. 基本思想
- 二. 快速排序
- 2.1 hoare版本
- 2.2 挖坑法
- 2.3 前后指针法
- 2.4 快速排序优化
- 三数取中法取key(hoare版本)
- 小区间优化
一. 基本思想
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
二. 快速排序
2.1 hoare版本
思路:
1.让key==数组在特定区间的第一个元素的下标
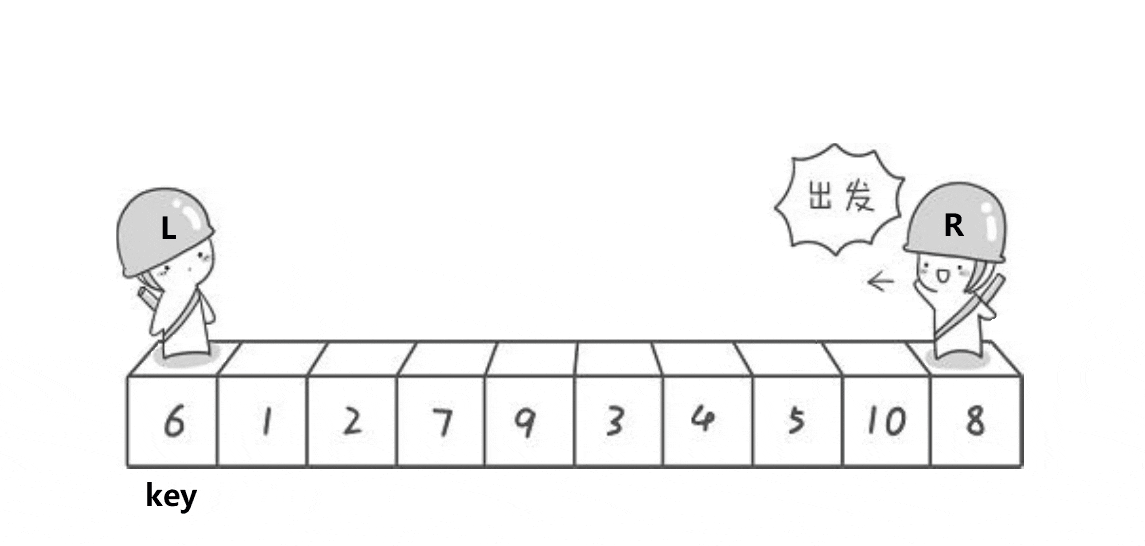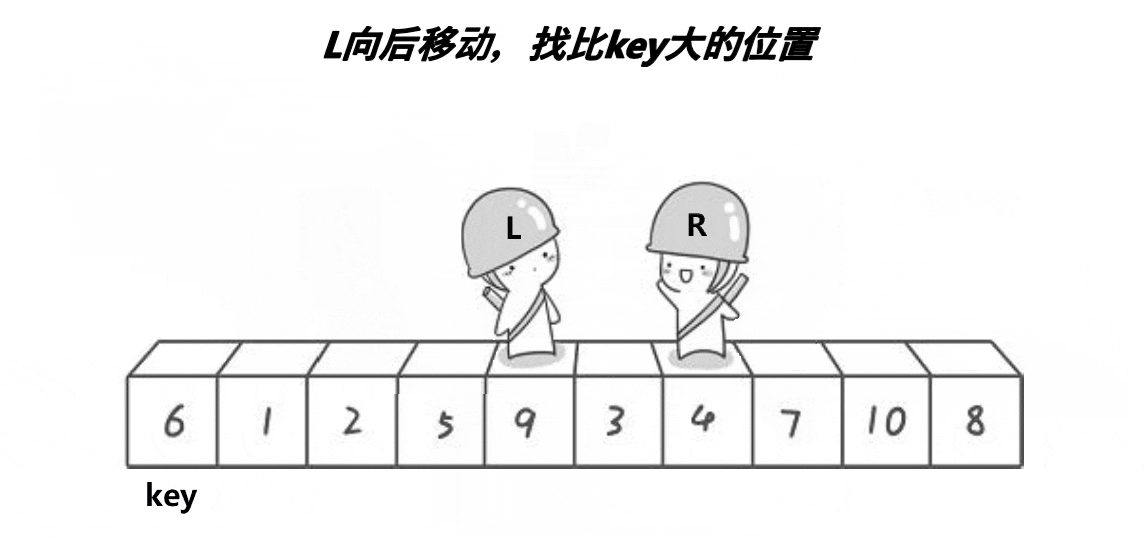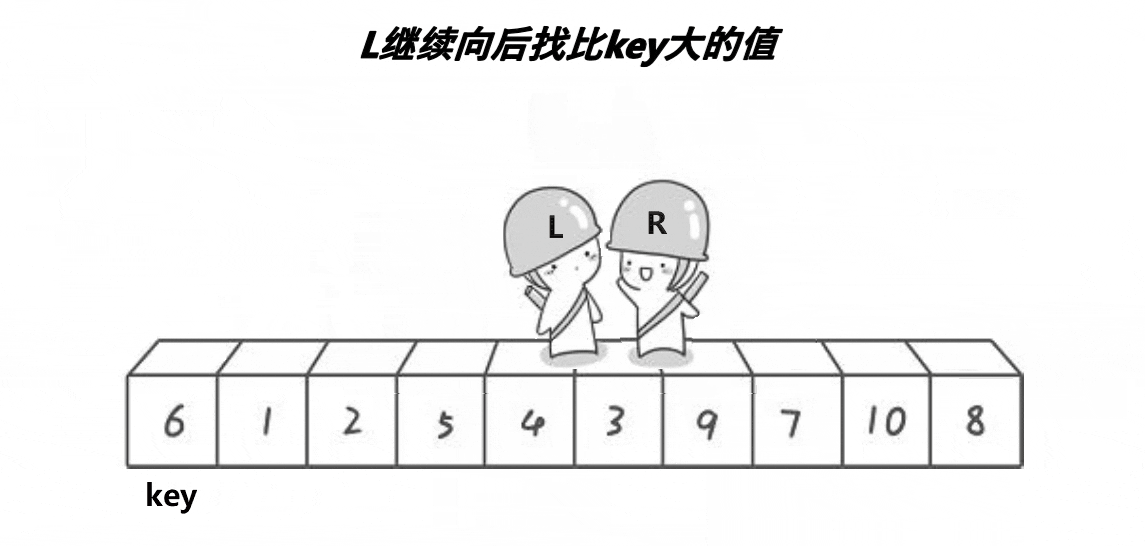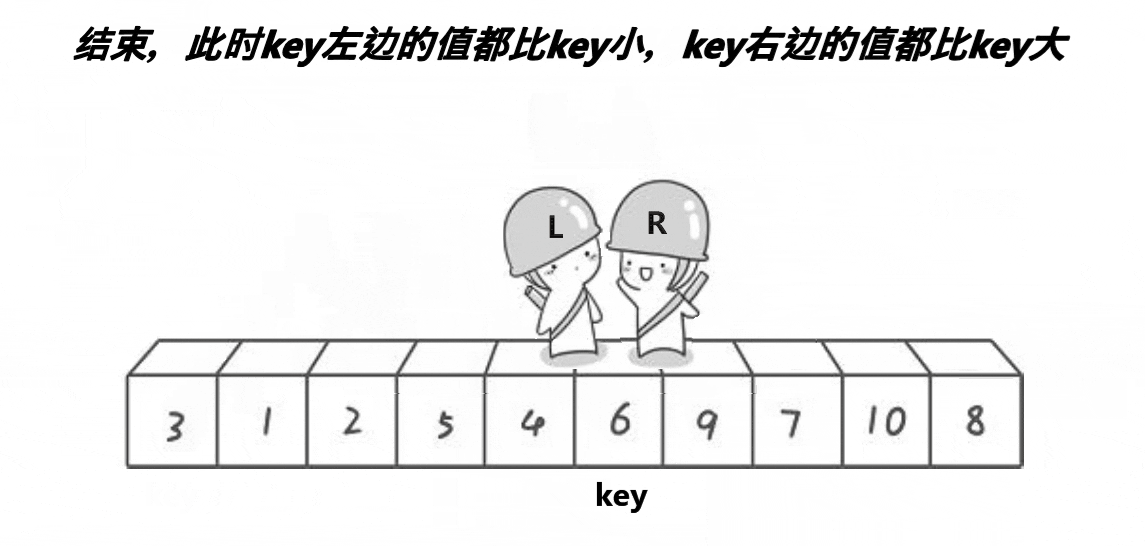
2.定义变量left和right,它们分别初始化为数组在特定区间的首元素和最后一个元素的下标,right先向前走,找到比key小的位置后停下;left再走,找到比key大的位置后停下;交换下标为right和left数组元素的位置。这样大的值就被放在后面,小的值就被放在前面
3.等到left和right相遇时,将相遇位置a[left]和下标为key的元素a[key]交换位置(能保证a[left]<a[key],具体原因下面会讲)
4.1-3步完成后,相遇位置即a[key]左边全是<=它的,右边都是>=它的
5.递归a[key]的左右子树,让它们经历1-3步
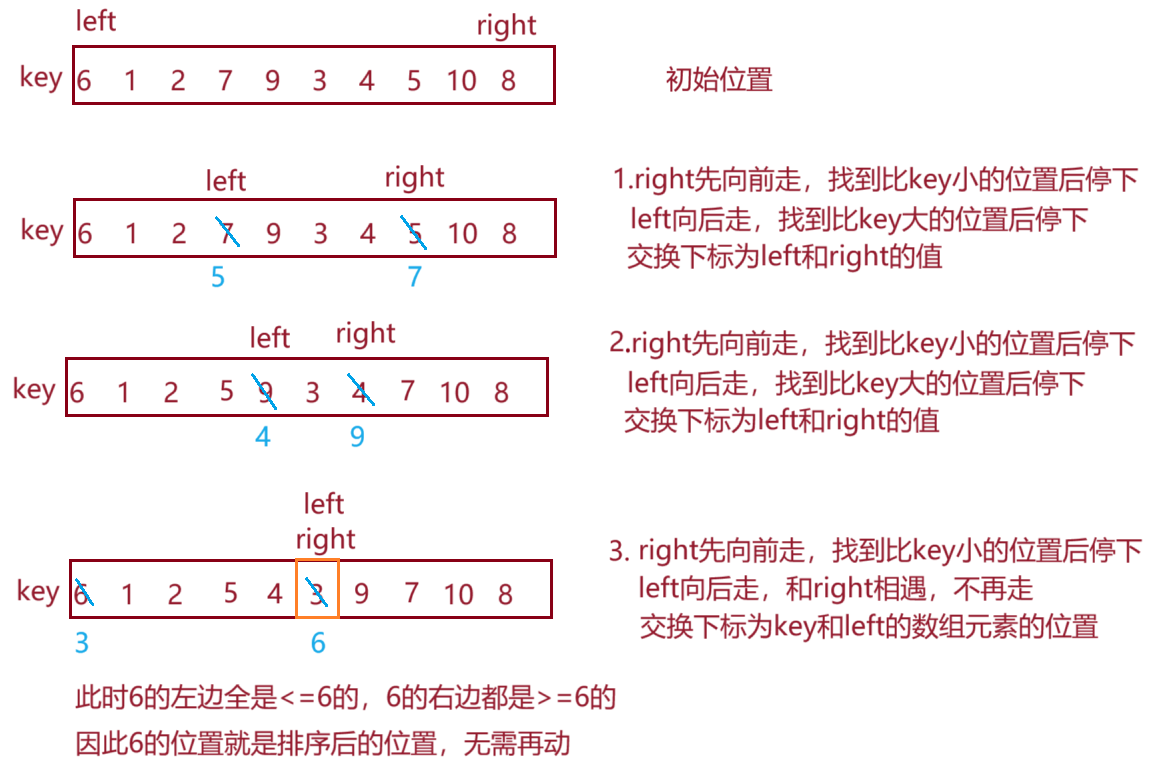
上面这幅图展示了将一个元素排序的步骤,后面还要排序6的左边和右边,我们可以将它当成一个二叉树来处理。第二次我们先来排6的左子树

第三次我们再来排3的左子树

2的左右子树分别为一个元素和空,所以不需要再递归下去。这两种情况用代码实现为:
if (begin >= end)return;
再递归3的右子树和6的右子树,思路一样,就不再赘述了
相遇位置的值一定小于下标为key的数组元素的原因:

int PartSort1(int* a, int begin, int end)
{int key = begin;int left = begin;int right = end;//right先走,left后走,right找小,left找大while (left < right){while (left < right && a[right] >= a[key])right--;while (left < right && a[left] <= a[key])left++;Swap(&a[left], &a[right]);}Swap(&a[key], &a[left]);return left;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int key = PartSort1(a, begin, end);QuickSort(a, begin, key - 1);QuickSort(a, key + 1, end);
}
2.2 挖坑法
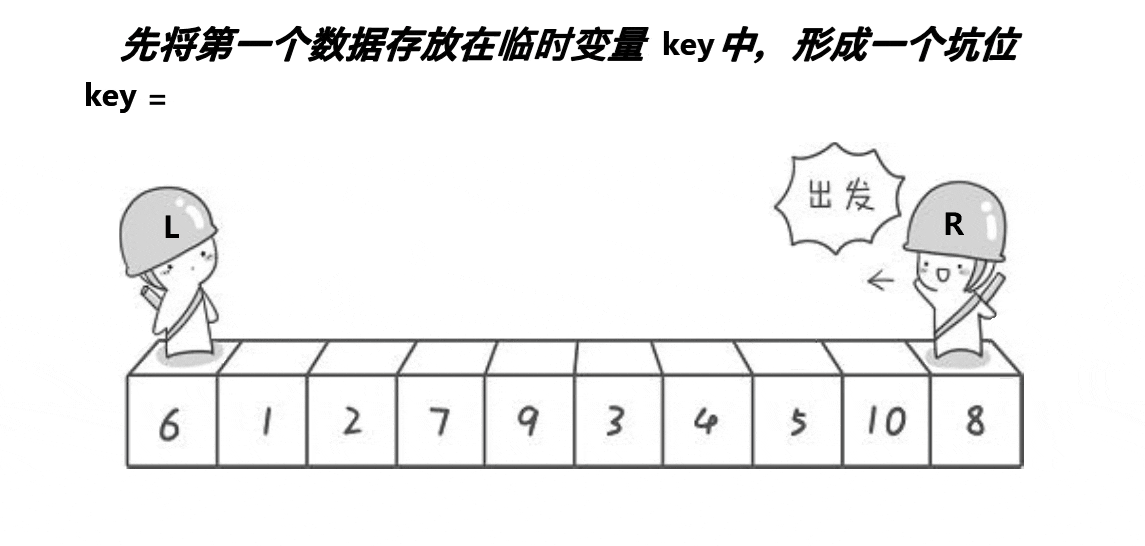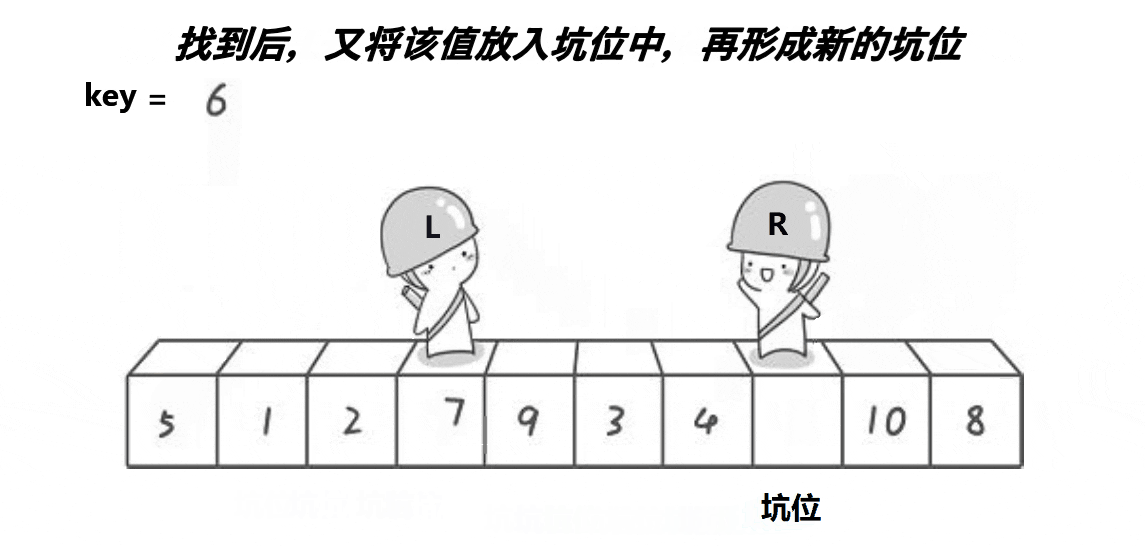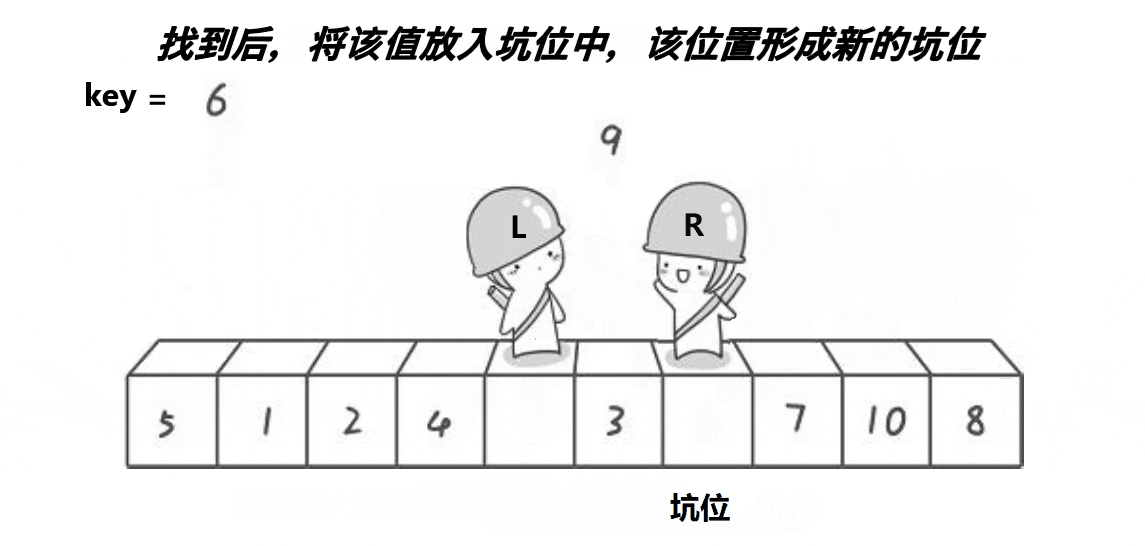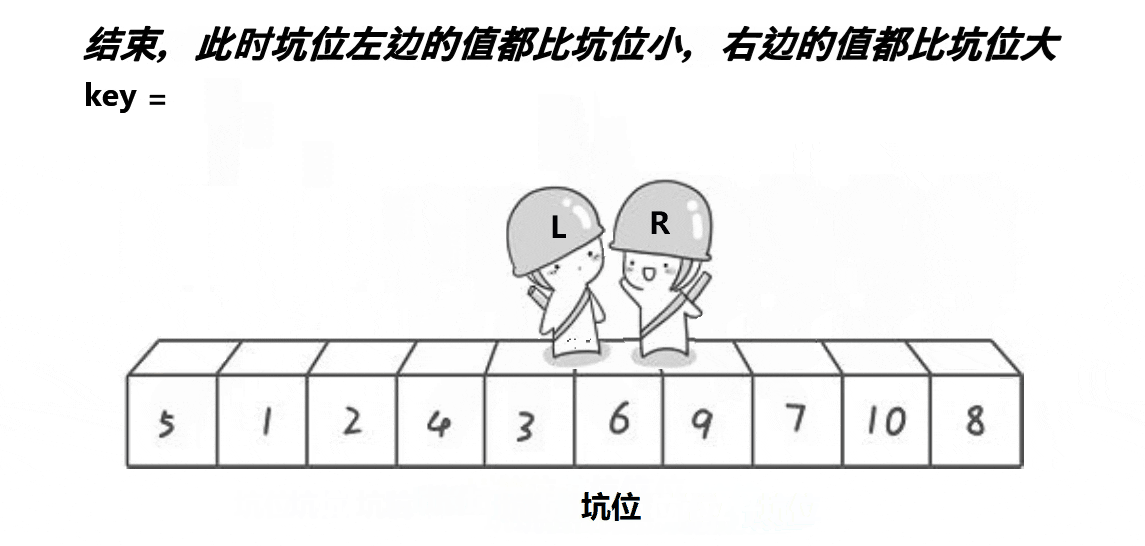
思路:

挖坑法实际上与hoare方法差不多,只是可能更好理解一些。接下来也是递归6的左右子树,不多说了
int PartSort2(int* a, int begin, int end)
{int left = begin;int right = end;int hole = begin;int key = a[hole];while (left < right){while (left < right && a[right] >= key)right--;a[hole] = a[right];hole = right;while (left < right && a[left] <= key)left++;a[hole] = a[left];hole = left;}a[hole] = key;return hole;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int key = PartSort2(a, begin, end);QuickSort(a, begin, key - 1);QuickSort(a, key + 1, end);
}
2.3 前后指针法

思路:
1.定义3个变量key,prev和cur来表示数组的下标,prev和key置为第一个元素的下标,cur置为第二个元素的下标
2.当a[cur]>=a[key]时,cur++
3.当a[cur]<a[key]时,prev++,交换下标为prev和cur的元素,再cur++
4.如果cur>end(最后一个元素的下标),交换下标为prev和key的元素
5.递归a[key]的左右子树,让它们经历1-4步

接下来也是递归6的左右子树,不多说了
int PartSort3(int* a, int begin, int end)
{int key = begin;int prev = begin;int cur = begin + 1;while (cur <= end){if(a[cur]<a[key]){prev++;Swap(&a[prev], &a[cur]);}cur++;}Swap(&a[prev], &a[key]);return prev;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int key = PartSort3(a, begin, end);QuickSort(a, begin, key - 1);QuickSort(a, key + 1, end);}
2.4 快速排序优化
1
三数取中法取key(hoare版本)
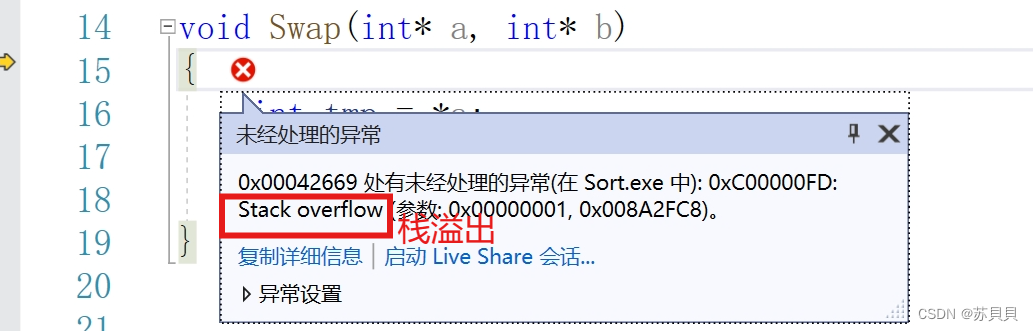
当数组本来就是有序数组(如升序)时,hoare版本的排序后的key相当于只有右子树,没有左子树。这样在数组元素较多时(如10000个),在debug条件下可能会因为栈溢出而报错(在release条件下不会,因为release对递归建立栈帧的优化已经足够好了)
下面是测试排序性能的函数,将用希尔排序排序好的数组a1再用快速排序,发现会报错,原因:栈溢出
void TestOP()
{srand(time(0));const int N = 10000;int* a1 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();}int begin1 = clock();ShellSort(a1, N);int end1 = clock();int begin2 = clock();QuickSort(a1, 0, N-1);int end2 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);free(a1);
}
那下面我们来优化hoare版本的快速排序。我们不再取数组第一个元素为key,而是取a[begin],a[end]和a[midi](midi是中间元素的下标)三者中的中位数。如何实现呢?先找到中位数的下标,再交换第一个元素和中位数的位置,再让key==begin,此时a[key]就不会是最小的元素了
int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;if (a[begin] > a[midi]){if (a[midi] > a[end])return midi;else if (a[end] > a[begin])return begin;elsereturn end;}else{if (a[end] > a[midi])return midi;else if (a[begin] > a[end])return begin;elsereturn end;}
}int PartSort1(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[begin], &a[midi]);int key = begin;int left = begin;int right = end;//right先走,left后走,right找小,left找大while (left < right){while (left < right && a[right] >= a[key])right--;while (left < right && a[left] <= a[key])left++;Swap(&a[left], &a[right]);}Swap(&a[key], &a[left]);return left;
}
2
小区间优化
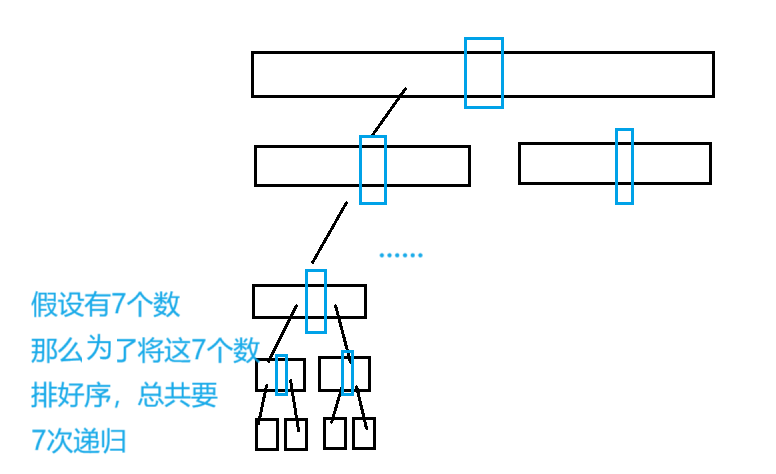
假设每次的key的最终位置都是中间位置,那么为了将最后7个数排好序,总共要递归7次,这种代价还是有些大的,所以我们选择当要排列的数组的元素比较少时,采用直接插入排序
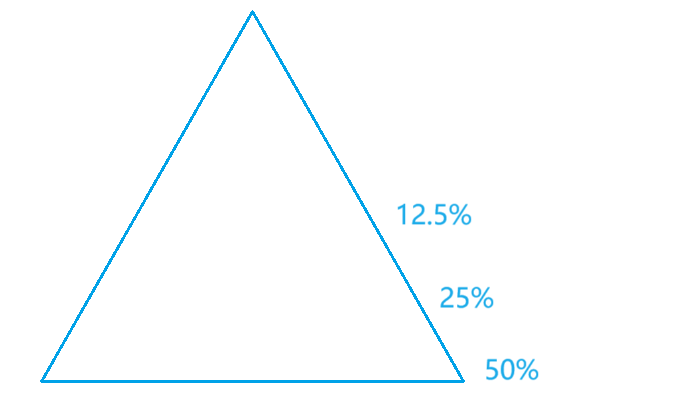
那当要排列的数组的元素小于多少时用直接插入排序呢?我们一般选择在树的倒数前3排开始,因为这3排(如果是满二叉树),那么会占据整个树的将近90%的元素。因为最后一层的元素个数为2^(h-1),总元素个数为2 ^h-1,所以将近占了一半的元素,倒数第二排是倒数第一排的一半,所以是25%……基于这种原因,我们最后选择当要排列的数组的元素小于10时用直接插入排序,当然,你也可以选择其他的值
代码如下,你能发现有什么问题吗?
void QuickSort1(int* a, int begin, int end)
{if (begin >= end)return;if (end - begin + 1 < 10)InsertSort(a, end - begin + 1);else{int key = PartSort1(a, begin, end);QuickSort1(a, begin, key - 1);QuickSort1(a, key + 1, end);}
}
直接插入排序本来是从begin的位置开始到往后的end - begin + 1个元素结束,但是上面的代码是从下标为0的位置开始,所以将它改正
void QuickSort1(int* a, int begin, int end)
{if (begin >= end)return;if (end - begin + 1 < 10)InsertSort(a + begin, end - begin + 1);else{int key = PartSort1(a, begin, end);QuickSort1(a, begin, key - 1);QuickSort1(a, key + 1, end);}
}void QuickSort2(int* a, int begin, int end)
{if (begin >= end)return;int key = PartSort1(a, begin, end);QuickSort2(a, begin, key - 1); QuickSort2(a, key + 1, end);
}
再使用测试排序性能的函数看看优化后与优化前的差别
void TestOP()
{srand(time(0));const int N = 10000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];}int begin1 = clock();QuickSort1(a1, 0, N - 1);int end1 = clock();int begin2 = clock();QuickSort2(a2, 0, N - 1);int end2 = clock();printf("QuickSort1(优化后):%d\n", end1 - begin1);printf("QuickSort2:%d\n", end2 - begin2);free(a1);free(a2);
}
在debug条件下的结果:

我们发现,优化后只是比没有优化快了2毫秒,好像并没有很优秀。这也是正常的,毕竟快速排序本身就是一个较好的排序,相当于你本身就靠了93分,再让你提高5分,是不是也不容易呢?
好了,那么本篇博客就到此结束了,如果你觉得本篇博客对你有些帮助,可以给个大大的赞👍吗,感谢看到这里,我们下篇博客见❤️



)


)













