【算法杂货铺】分治

🌈前言🌈

📁 快速排序

📂75. 颜色分类 - 力扣（LeetCode）

📂 912. 排序数组 - 力扣（LeetCode）

📂 215. 数组中的第K个最大元素 - 力扣（LeetCode）

📂 面试题 17.14. 最小K个数 - 力扣（LeetCode）

📁 归并排序

📂 912. 排序数组 - 力扣（LeetCode）

📂 LCR 170. 交易逆序对的总数 - 力扣（LeetCode）

📂 315. 计算右侧小于当前元素的个数 - 力扣（LeetCode）

📂 493. 翻转对 - 力扣（LeetCode）

📁 总结

🌈前言🌈

欢迎收看本期【算法杂货铺】，本期内容将讲解分治思想，通过讲解快速排序和归并排序这两个排序来理解学习分治。

本文旨在零基础学习，轻松搞懂，所以会不会讲解算法时间复杂度等验证，而是给出结论。当然，习题是会给出题解和思路的。

此外，本文中所有代码都是C++实现，其他语言可以参考题解思路。

为了照顾没有学习过快速排序的同学，本文会在讲解习题之前，讲解排序思路。

📁 快速排序

快速排序的思想是选择一个基准元素key，以key为中间值，将数组分为两个区间，左区间的元素是严格小于key值，右区间元素严格大于key值。

再将左区间和右区间排序，也是同样的思路，选出key值，划分左右区间，再进行排序。

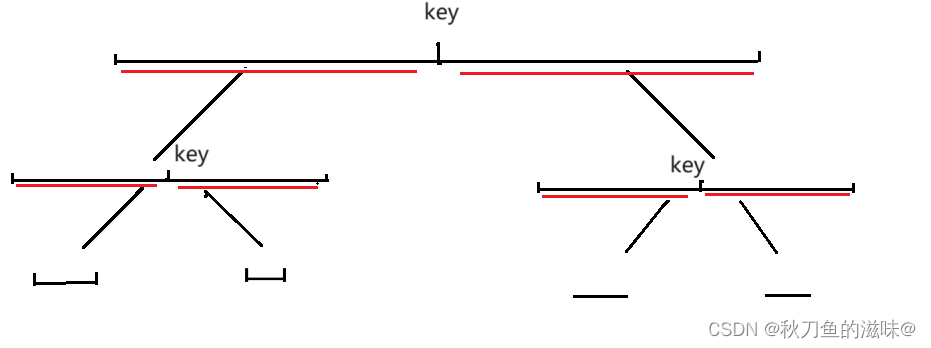
由上图可知，我们每次将数组排序，都将数组划分成两个区间，一共会执行logN层，每一层都会遍历n次，所以时间复杂度是O(NlogN)。

快速排序的实现：三指针（数组分三块） + 随机选择基准元素。

📂75. 颜色分类 - 力扣（LeetCode）

在讲解快速排序之前，我们首先来学习一下，怎么将每一层的数组排序，即三指针（数组分三块）。

这里我们使用三个指针（下标）来讲区间划分。

left : 表示0元素的末尾。

cur ：用来扫描数组。

right : 表示2的开头。

扫描期间，cur要保证以下区间的稳定：

[0,left] : 都是0元素；

[left + 1 , cur - 1] : 都是1元素；

[cur , right - 1] : 是未扫描元素。

[right , size()-1] : 是2元素。

算法流程：

i. 初始化left = -1 , cur =0 , right = size() + 1；

ii. 循环扫描数组，cur < right时，cur就继续往后扫描数组。

a. nums[cur] == 0时，就交换nums[left + 1] 和 nums[cur]，再让left++,cur++。cur为什么可以++，因为left+1位置的元素，一定为0，或者1的。1的话，我们直接++即可；如果是0，就1种情况，cur == left + 1,所以是自己与自己交换，也可以直接++。

b. nums[cur] == 1时，cur直接++。

c. nums[cur] == 2时，交换nums[right - 1] 和 nums[cur]，right--, 此时cur不能++，因为不能保证right-1位置的值一定是0 或者 1，所以需要接着判断交换后，i位置的值。

iii. cur >= right 表示扫描结束，此时总共有三个区间，分别代表0,1,2的区间。

class Solution {
public:void sortColors(vector<int>& nums) {int left = -1 , cur = 0 , right = nums.size();while(cur < right){if(nums[cur] == 0)swap(nums[++left] , nums[cur++]);else if(nums[cur] == 1)cur++;else    swap(nums[--right],nums[cur]);}}
};

📂 912. 排序数组 - 力扣（LeetCode）

如果你理解颜色分类这道题，那么你以及掌握快速排序的大部分内容了，剩下的就是理解如果将区间划分，以及选择基准元素了。

选择基准元素，最佳的策略是随机选择[left,right]范围内的任意元素，对应的是rand()函数，这样时间复杂度会达到最优解。

将一层排完序后，再递归到左右区间进行排序。

class Solution {
public:vector<int> sortArray(vector<int>& nums) {srand(time(NULL));qsort(nums , 0 , nums.size()-1);return nums;}void qsort(vector<int>& nums,int l ,int r){if(l >= r)return;int key = GetRandom(nums,l,r);int left = l - 1 , right = r + 1;int cur = l;while(cur < right){if(nums[cur] < key)swap(nums[++left], nums[cur++]);else if(nums[cur] == key)cur++;else    swap(nums[--right],nums[cur]);}qsort(nums,l,left);qsort(nums,right,r);}int GetRandom(vector<int>& nums,int left,int right){return nums[rand()%(right - left + 1) + left];}
};

📂 215. 数组中的第K个最大元素 - 力扣（LeetCode）

通过快速排序，我们将区间划分成三块[0,left] [left + 1 , right - 1] [right , size()-1]。计算出每个区间元素个数，再到相应区间去找即可。

算法就是快速选择算法。

class Solution {
public:int findKthLargest(vector<int>& nums, int k) {srand(time(NULL));return qsort(nums , 0 , nums.size() - 1 , k);}int qsort(vector<int>& nums,int l , int r , int k){if(l == r)  return nums[l];int key = GetRandom(nums,l,r);int left = l - 1 , right = r + 1;int cur = l;while(cur < right){if(nums[cur] < key)swap(nums[++left],nums[cur++]);else if(nums[cur] == key)cur++;elseswap(nums[--right],nums[cur]);}int c = r - right + 1;int b = right - left - 1;if(c >= k )return qsort(nums,right,r,k);else if(b + c >= k)return key;else return qsort(nums,l,left,k-b-c);}int GetRandom(vector<int>& nums, int left , int right){return nums[rand()%(right - left + 1) + left];}
};

📂 面试题 17.14. 最小K个数 - 力扣（LeetCode）

依旧，是一道快速选择算法的题目，不过是从前面开始，并且是选k个数，那我们就将排好序的前k个数返回即可。顺序没有要求。

顺序没有要求，意味着当k落在[left + 1, right - 1]这个区间的时候，直接返回即可。因为左边两个区间所有元素都是小于左区间的。

class Solution {
public:vector<int> smallestK(vector<int>& arr, int k) {srand(time(NULL));qsort(arr, 0 , arr.size()-1 , k);return {arr.begin() , arr.begin() + k};}void qsort(vector<int>& nums,int l,int r,int k){if(l >= r)return;int key = GetRandom(nums,l,r);int left = l - 1, right = r + 1;int cur = l;while(cur < right){if(nums[cur] < key)swap(nums[++left],nums[cur++]);else if(nums[cur] == key)cur++;else    swap(nums[--right] , nums[cur]);}int a = left - l + 1;int b = right - left - 1;if(a >= k)qsort(nums,l,left,k);else if(a + b >= k)return ;else    qsort(nums,right,r,k-a-b);}int GetRandom(vector<int>& nums,int left , int right){return nums[rand() % (right - left + 1) + left];}
};

📁 归并排序

📂 912. 排序数组 - 力扣（LeetCode）

归并排序，非常充分的体现了分治思想，根据元素个数将数组划分成两个区间，直到只有1个元素，使整个数组的排序分为【左半部分排序】和【右半部分排序】。

归并排序和快速排序有什么区别呢？归并排序是先将左区间排序，再将右区间排序，最后整体排序，是一种后序遍历的思路。快速排序是先将元素放在合适位置后，即先整体排序，再将左右区间排序，是一种前序遍历的思路。

当然，还有就是归并排序是要有辅助数组的。

class Solution {
public:vector<int> temp;vector<int> sortArray(vector<int>& nums) {temp.resize(nums.size());mergesort(nums,0,nums.size()-1);return nums;}void mergesort(vector<int>& nums,int left,int right){if(left >= right)return ;int mid = (left + right) >>1;mergesort(nums,left,mid);mergesort(nums,mid+1 ,right);int cur1 = left,cur2 = mid+1;int i = left;while(cur1 <= mid && cur2 <= right){if(nums[cur1] <= nums[cur2]){temp[i++] = nums[cur1++];}else{temp[i++] = nums[cur2++];}}while(cur1 <= mid){temp[i++] = nums[cur1++];}while(cur2 <= right){temp[i++] = nums[cur2++];}for(int i= left ; i <= right ;i++)nums[i] = temp[i];}
};

📂 LCR 170. 交易逆序对的总数 - 力扣（LeetCode）

逆序对的概念就是有两个元素,后面的元素小于前一个元素。本期就是统计逆序对的个数，如果我们采用暴力解法，即从当前位置开始，往后遍历，找到比它小的就+1，肯定是不行的，时间复杂度为O(N^2)。

用归并排序求逆序数是很经典的方法，主要是在归并排序的合并过程中统计处逆序的数量，也就是在合并两个有序序列的过程中，能快速求出逆序对的数量。

1. 为什么可以利用归并排序：

将数组划分成两个，可以将逆序对产生的方式划分为3组：1. 全部从左数组来；2. 全部从右数组来；3. 左右数组各一个。根据排列组合的分类相加原理，三种情况下产生的逆序对总和，正好是总的逆序对的个数。

这个思路正好匹配归并排序：1. 先排序做数组；2. 再排序有数组；3. 左右数组合并。

因此，我们可以利用归并排序的过程，先求出左数组中逆序对的数量，再求出右数组中逆序对的个数，最后求出左右数组各一个逆序对的数量，三者相加即可。

2. 为什么要用归并排序

在归并排序过程中，我们得到的是两个有序数组，可以利用数组的有序性，快速统计出逆序对的数量，而不是将所有情况枚举出来。

有两个策略：

1. 快速统计出某个数字前面有多少个数比它大；（升序）

2. 快速统计出某个数组后面有多少个数比它小；（降序）

这里的顺序是不能改变的，升序不能改为降序，可以理解为如果升序改为降序，可能会有重复的计算。

class Solution {
public:int temp[50010];int reversePairs(vector<int>& record) {return mergesort(record , 0 , record.size()-1);}int mergesort(vector<int>& nums, int left , int right){if(left >= right)return 0;int ret = 0;int mid = (left + right) >> 1;ret += mergesort(nums,left,mid);ret += mergesort(nums,mid+1,right);int cur1 = left , cur2 = mid+1;int i = left;while(cur1 <= mid &&cur2 <= right){if(nums[cur1] <= nums[cur2]){temp[i++] = nums[cur1++];}else{ret += mid - cur1 + 1;temp[i++] = nums[cur2++];}}while(cur1 <= mid){temp[i++] = nums[cur1++];}while(cur2 <= right){temp[i++] = nums[cur2++];}for(int i= left ; i <= right ;i++){nums[i] = temp[i];}return ret;}
};

📂 315. 计算右侧小于当前元素的个数 - 力扣（LeetCode）

各个数组和函数功能

1. 创建两个全局数组：

vector<int> index : 记录下标

vector<int> ret : 记录结果

inde用来与原数组与对应位置的元素绑定，ret用来记录每个位置统计出来的逆序对的个数。

并创建index和ret的辅助数组。

2. countsamller()主函数：

a. 初始化两个全局数组，index初始化为数组的下标，ret初始化为0。

b. 为两个数组开辟大小为n的空间。

c. 调用mergesort()函数，并返回ret结果数组。

3. mergesort()函数

a. 定义递归出口：left>=right，直接返回。

b. 划分区间 [left , mid] 和 [mid + 1 ， right]。

c. 统计左右区间逆序对数量

d. 统计左右区间逆序对数量。

class Solution {
public:vector<int> ret;vector<int> index;vector<int> indexTemp;vector<int> retTemp;vector<int> countSmaller(vector<int>& nums) {ret.resize(nums.size());index.resize(nums.size());indexTemp.resize(nums.size());retTemp.resize(nums.size());for(int i=0;i<nums.size();i++){ret[i] = 0;index[i] = i;}mergesort(nums, 0 , nums.size()-1 , ret);return ret;}void mergesort(vector<int>& nums,int left,int right,vector<int>& ret){if(left >= right)return;int mid = (left + right) >> 1;//处理左区间逆序对mergesort(nums,left,mid,ret);//处理右区间逆序对mergesort(nums,mid+1,right,ret);//处理一左一右int cur1 = left,cur2 = mid+1;int i = left;while(cur1 <= mid && cur2 <= right){if(nums[cur1] <= nums[cur2])                {retTemp[i] = nums[cur2];indexTemp[i++] = index[cur2++];}else{ret[index[cur1]] += right - cur2 +1;retTemp[i] = nums[cur1];indexTemp[i++] = index[cur1++];} }//处理剩余排序问题while(cur1 <= mid){retTemp[i] = nums[cur1];indexTemp[i++] = index[cur1++];}while(cur2 <= right){retTemp[i] = nums[cur2];indexTemp[i++] = index[cur2++];           }for(int i=left;i<=right;i++){nums[i] = retTemp[i];index[i] = indexTemp[i];}}
};

📂 493. 翻转对 - 力扣（LeetCode）

翻转对和逆序对的定义大同小异，你对许是前面的数要大于后面的数。而翻转数是前面的一个数要大于后面某个数的两倍。因此，我们可以采用归并排序来解决问题。

与逆序对最大的不同在于，求逆序对时，可以在归并的时候统计逆序对的数量。而翻转对则需要提前统计。

class Solution {
public:int temp[50010];int reversePairs(vector<int>& nums) {return mergesort(nums , 0 , nums.size()-1);}int mergesort(vector<int>& nums,int left,int right){if(left >= right)return 0;int ret = 0;int mid =(left + right) >> 1;ret += mergesort(nums,left,mid);ret += mergesort(nums,mid+1,right);//计算翻转对int cur1 = left,cur2 = mid+1;while(cur1 <= mid){//while(cur2 <= right && nums[cur2] >= nums[cur1] / 2.0) cur2++;while(cur2 <= right && nums[cur2] >= nums[cur1] / 2.0){cur2++;}if(cur2 > right){break;}ret += right - cur2 + 1;cur1++;}//合并有序数组cur1 = left,cur2 = mid+1;int i = left;while(cur1 <= mid && cur2 <= right){temp[i++] = nums[cur1] <= nums[cur2] ? nums[cur2++]:nums[cur1++];}while(cur1 <= mid){temp[i++] = nums[cur1++];}   while(cur2 <= right){temp[i++] = nums[cur2++];}for(int i= left ;i <= right ; i++){nums[i] = temp[i];}return ret;}
};