程序猿成长之路之番外篇——矩阵算法

今天在复习线性代数知识的过程中，用java语言简单实现了一下矩阵算法。

数学知识回顾

1.什么是矩阵
在数学领域，矩阵就像一个表格，将数据排放进去，形成一个矩形。我们习惯用一个大括号把矩阵内的数据包括进来。

1.矩阵
在数学领域，矩阵就像一个表格，将数据排放进去，形成一个矩形。我们习惯用一个大括号把矩阵内的数据包括进来。

2. 矩阵的运算
矩阵可以进行加法、乘法运算，如果是个方形矩阵也可以转置或者求逆。此外，加法和乘法都有结合律、分配律等定律。

矩阵加法运算：
在这里插入图片描述
矩阵乘法运算：
运算规则相对较为繁琐：

  1. A(m,n) * B(n,k) = C(m,k) // 具有m行n列的矩阵A 乘以具有n行k列的矩阵B结果为m行k列的矩阵c
  2. 运算过程如下图：就拿C(1,1) – 结果矩阵的第一行第一列的元素来说，它等于A(1,1) * B(1,1) + A(1,2) * B(2,1) = 1 * 2 + 2 * 6 = 14
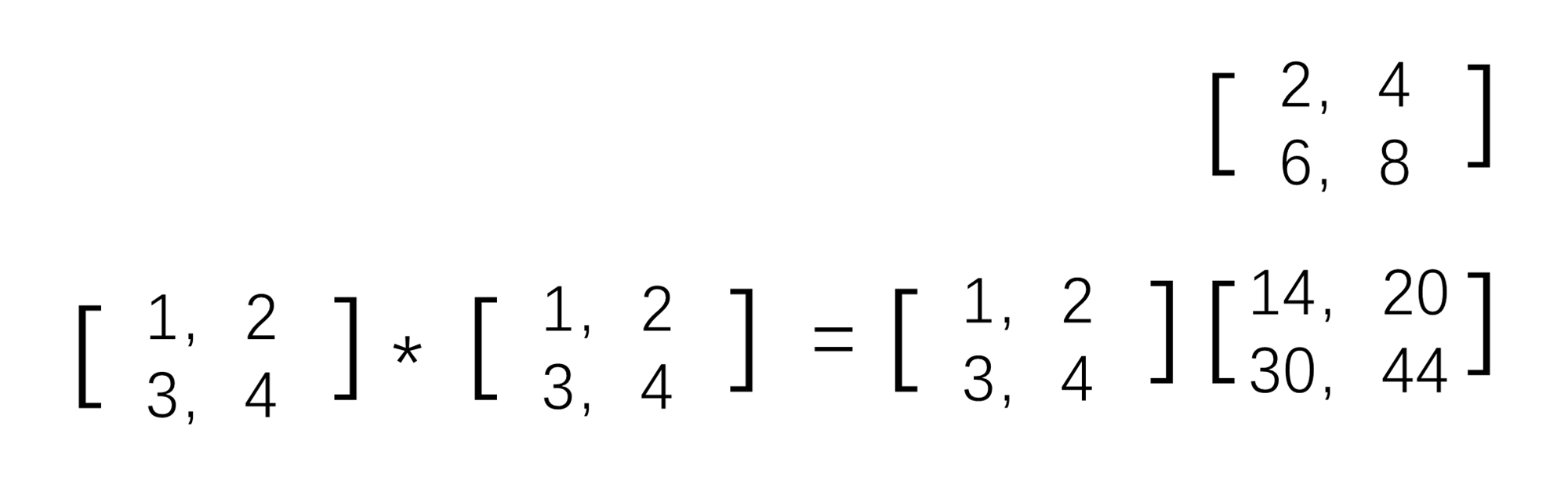
    在这里插入图片描述
  3. 矩阵的转置
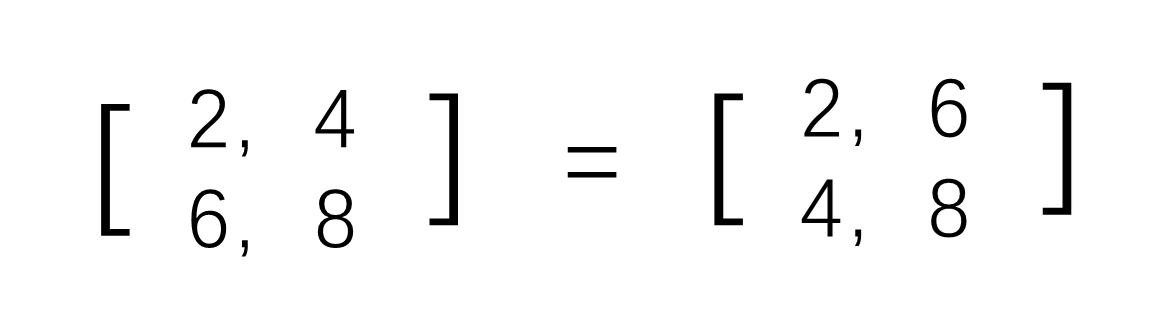
    在这里插入图片描述
  4. 矩阵求逆
    我们知道伴随矩阵 = Det(矩阵A) * 矩阵的逆
    我们又知道 伴随矩阵 = Σ(Aij 的代数余子式), i,j∈（0,size))
    因此可以求出矩阵的逆 = |伴随矩阵| / Det(矩阵A)
    求逆的难点在于获取代数余子式。

算法实现

  1. 编写matrix类
package matrixUtils;import java.util.Arrays;class Matrix {@Overridepublic String toString() {String str = "";for (int i = 0; i < arr.length;i++) {str += Arrays.toString(arr[i]);str +="\n";}return str;}//宽度private final int width;//高度private final int height;//数组private final double[][] arr;Matrix(int width, int height) {this.width = width;this.height = height;arr = new double[height][width];}Matrix(int width, int height, double[][] arr) {this.width = width;this.height = height;this.arr = arr;}public int getWidth() {return width;}public int getHeight() {return height;}public double[][] getArr() {return arr;}public void setArrVal(int x, int y, double val) {arr[x][y] = val;}public boolean compareTo(Matrix matrix) {//比较return this.width == matrix.width & this.height == matrix.height;}public void setArrVals(int startIndex, int[][] val) {int size = val[0].length;size *= val.length;if (startIndex < 0 || size <= 0){return;}//count计数器for (int i = 0; i < size;i++) {arr[i / val[0].length][i % val[0].length] = val[i/val[0].length][i % val[0].length];}}}
  1. 编写工厂类
public class MatrixFactory {private static final int MAX_SIZE = 1 << 30;/*** 获取实例*/public static Matrix getInstance(int width, int height) {if (width < 0 || width > MAX_SIZE) {throw new IllegalArgumentException("宽度有误");}if (height < 0 || height > MAX_SIZE) {throw new IllegalArgumentException("高度有误");}return new Matrix(width, height);}public static Matrix getInstance(int width, int height, double[][] arr) {if (width < 0 || width > MAX_SIZE) {throw new IllegalArgumentException("宽度有误");}if (height < 0 || height > MAX_SIZE) {throw new IllegalArgumentException("高度有误");}return new Matrix(width, height, arr);}
}
  1. 矩阵乘法
    设计思路：设置一个计数器m，用于获取结果的列值，当m == matrix2的宽度时，也就是说当前已经完成对i行的处理，结果保存进matrix中，让i（行数）加1并且m重置为0，否则让结果列数自加。
	/*** 矩阵相乘* @param matrix* @return*/public static Matrix multiply(Matrix matrix1,Matrix matrix2) {//生成一个新的矩阵if (matrix1 == null || matrix2 == null) {throw new IllegalArgumentException("矩阵不匹配，请检查");}if (matrix1.getWidth() != matrix2.getHeight()) {throw new IllegalArgumentException("矩阵不匹配，请检查");}//新建一个矩阵Matrix resMatrix = MatrixFactory.getInstance(matrix2.getWidth(),matrix1.getHeight());int m = 0; //m - matrix2的列数for (int i = 0; i < matrix1.getHeight();) {int sum = 0; //sum - 求和for(int j = 0; j < matrix1.getWidth(); j++) {/*** 按照matrix1 第i行 * matrix2 第m列 得到结果保存*/sum += matrix1.getArr()[i][j] * matrix2.getArr()[j][m];}resMatrix.setArrVal(i, m, sum);if (m == matrix2.getWidth() - 1) {i++;m=0;} else {m++;}}return resMatrix;}
  1. 矩阵转置
    设计思路： arr[i][j] == arr[j][i]。(i,j位置上的数据互换）
/*** 矩阵反转* @param matrix* @return*/public static Matrix reverse(Matrix matrix) {//生成一个新的矩阵if (matrix == null) {throw new IllegalArgumentException("矩阵不匹配，请检查");}//生成一个新的矩阵Matrix resMatrix = MatrixFactory.getInstance(matrix.getHeight(), matrix.getWidth());for(int i =0; i <matrix.getHeight();i++) {for (int j = 0; j < matrix.getWidth(); j++) {//如果行列值一样就跳过if (i == j) {resMatrix.setArrVal(i, j, matrix.getArr()[i][j]);continue;}resMatrix.setArrVal(j, i, matrix.getArr()[i][j]);}}return resMatrix;}
  1. 矩阵求det
    设计思路：利用递归，每次的余子式size-1，到了size为2时就直接使用余子式公式进行计算。
/*** 获取矩阵det* @param matrix* @return*/public static double getMatrixDet(Matrix matrix) {if (matrix == null) {throw new IllegalArgumentException("矩阵不匹配，请检查");	}int height = matrix.getHeight();int width = matrix.getWidth();if (height != width) {throw new IllegalArgumentException("矩阵不匹配，请检查");	}return getMatrixDet(matrix,width);}/*** 获取矩阵det* @param matrix* @param width* @return*/private static double getMatrixDet(Matrix matrix, int size) {if (size <= 1) {return matrix.getArr()[0][0];} else if (size == 2) {return matrix.getArr()[0][0] * matrix.getArr()[1][1] - matrix.getArr()[0][1] * matrix.getArr()[1][0];}// 计算det,每次分解成大小为size-1的数组int det = 0;double[][] arr = matrix.getArr();for(int i = 0; i < arr[0].length; i++) {//获取余子式Matrix temp = getSubMatrix(0,i,size-1,arr);//统计det的值det += (Math.pow(-1, i)) * arr[0][i] * getMatrixDet(temp,size-1);}return det;}/*** 获取余子式* @param x - 要去除的第几行* @param y - 要去除的第几列* @param size 余子式size* @param arr 原数组* @return*/private static Matrix getSubMatrix(int x, int y,int size,double[][] arr) {//每次进行temp数组的填充Matrix temp = new Matrix(size,size);int addRow = 0; //填充计数for (int j = 0; j <= size; j++) {int addColumn = 0; //填充计数//跳过当前一行if (j == x) {addRow++;continue;}for (int m = 0; m < size + addColumn; m++) {//i列删除if (m == y) {addColumn++;continue;}//从第一行开始算，自动跳过第y列的数据temp.setArrVal(j-addRow,m - addColumn,arr[j][m]);}}return temp;}
  1. 矩阵求逆
    设计思路：利用公式 伴随矩阵 = det(矩阵) * 矩阵进行求解
/*** 求逆矩阵* @param matrix* @return*/public static Matrix inverse(Matrix matrix) {if (matrix.getWidth() != matrix.getHeight()) {throw new IllegalArgumentException("矩阵不匹配，请检查");}/*** AX = B* A-1AX=A-1A* X=A-1B*/int size = matrix.getHeight(); //sizedouble[][] arr = matrix.getArr(); //arr//结果矩阵Matrix resMatrix = MatrixFactory.getInstance(size,size);double det = getMatrixDet(matrix); //计算detfor (int i = 0; i < Math.pow(size,2); i++) { //size * size = length//获取每一项的余子式Matrix temp = getSubMatrix(i/size, i%size, size-1, arr);resMatrix.setArrVal(i/size, i%size, Math.pow(-1, i) * getMatrixDet(temp) / (det * 1.0)); //计算余子式的det / 总det}return reverse(resMatrix); //转置}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/763171.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

FeignClient是否可以配置多个拦截器？

FeignClient是否可以配置多个拦截器？

1、做法 在Spring Cloud中&#xff0c;FeignClient是一个声明式的Web服务客户端&#xff0c;让调用远程服务就像调用本地方法一样简单。拦截器可以用于在发送请求之前或者获得响应之后执行一些操作&#xff0c;比如添加公共的Header、记录日志、做一些统计等。 在Feign中&…
阅读更多...
Python Web开发记录 Day14：Django part8 订单管理

Python Web开发记录 Day14：Django part8 订单管理

名人说：莫道桑榆晚，为霞尚满天。——刘禹锡（刘梦得，诗豪） 创作者：Code_流苏(CSDN)（一个喜欢古诗词和编程的Coder😊） 目录 1、数据库准备2、添加订单3、订单列表4、删除订单5、编辑订单6、补充解答1、数据库准备 1.修改models.py，添加Order订单表 models.py class O…
阅读更多...
JavaScript parseInt() 函数

JavaScript parseInt() 函数

JavaScript parseInt() 函数 从官方理解&#xff1a; parseInt() 函数解析字符串并返回整数。 radix 参数用于指定使用哪种数字系统&#xff0c;例如基数为 16&#xff08;十六进制&#xff09;表示字符串中的数字应从十六进制数解析为十进制数。 如果 radix 参数被省略&…
阅读更多...
【HTML面试题】src和href的区别

【HTML面试题】src和href的区别

一、请求资源不同 src 在请求资源时&#xff0c;会把这个资源下载下来href 建立链接通道&#xff0c;也就是引用元素和当前文档建立链接 二、作用结果不同 src 会替换当前元素href 只是引用资源和当前元素建立链接&#xff0c;所以不会替换当前内容。 三、浏览器解析方式不…
阅读更多...
3.21作业

3.21作业

#include<myhead.h> int do_add(sqlite3 *ppDb) { int xue0; char name[20]""; double coure0; char sql[128]""; printf("请输入学号\n"); scanf("%d",&xue); printf("请输入姓名\n&qu…
阅读更多...
Java SE

Java SE

java概述 1.什么是java java是一门面向对象的编程语言&#xff0c;作为静态面向对象编程语言&#xff0c;极好地实现了面向对象理论&#xff0c;允许程序员以优雅的思维方式进行复杂的编程 。 2.java语言有哪些特点&#xff1f; 2.1面向对象&#xff08;继承封装多多态&…
阅读更多...
SOCKS5是什么？

SOCKS5是什么？

SOCKS5是什么&#xff1f; SOCKS5&#xff0c;作为SOCKS网络协议家族的最新版本&#xff0c;是一种高级的网络协议&#xff0c;用于在客户端和服务器之间通过一个代理服务器交换网络包。它的设计考虑了多种网络环境&#xff0c;包括对IPv6和UDP协议的支持&#xff0c;并引入了…
阅读更多...
Uscrapper：一款功能强大的网络资源爬取工具

Uscrapper：一款功能强大的网络资源爬取工具

关于Uscrapper Uscrapper是一款功能强大的网络资源爬取工具&#xff0c;该工具可以帮助广大研究人员从各种网络资源中轻松高效地提取出有价值的数据&#xff0c;并且提供了稳定、友好且易于使用的UI界面&#xff0c;是安全研究人员和网络分析人员的强有力工具。 Uscrapper最大…
阅读更多...
漫谈5种注册中心

漫谈5种注册中心

01 注册中心基本概念 1.1 什么是注册中心&#xff1f; 注册中心主要有三种角色&#xff1a; 服务提供者&#xff08;RPC Server&#xff09;&#xff1a;在启动时&#xff0c;向 Registry 注册自身服务&#xff0c;并向 Registry 定期发送心跳汇报存活状态。 服务消费者&…
阅读更多...
哈希、散列表和Rabin-Karp算法

哈希、散列表和Rabin-Karp算法

字典 现有一个抽象数据类型(ADT)如下&#xff1a; 包括了一组元素&#xff0c;每个元素都有一个键key。假设没有元素拥有相同的key&#xff0c;如果有相同的key&#xff0c;则覆盖掉原有key的元素。 -insert(item) -delete(item) -search(key):根据给定的key&#xff0c;返…
阅读更多...
JetBrains全家桶激活，分享 GoLand 2024 激活的方案

JetBrains全家桶激活，分享 GoLand 2024 激活的方案

大家好&#xff0c;欢迎来到金榜探云手&#xff01; GoLand 公司简介 JetBrains 是一家专注于开发工具的软件公司&#xff0c;总部位于捷克。他们以提供强大的集成开发环境&#xff08;IDE&#xff09;而闻名&#xff0c;如 IntelliJ IDEA、PyCharm、和 GoLand等。这些工具被…
阅读更多...
第4周 Python程序流程控制刷题（循环结构）

第4周 Python程序流程控制刷题（循环结构）

单击题目&#xff0c;直接跳转到页面刷题&#xff0c;一周后公布答案。 P5722&#xff1a;数列求和B2054&#xff1a;求平均年龄B2059&#xff1a;奇数求和B2064&#xff1a;斐波那契数列B2077&#xff1a;角谷猜想B2098&#xff1a;整数去重B2128&#xff1a;素数个数 1. P5…
阅读更多...
力扣每日练习（3.20）补

力扣每日练习（3.20）补

322. 零钱兑换 想象你有一堆不同面值的硬币&#xff0c;现在的任务是用这些硬币凑出一个指定的金额&#xff0c;比如说11元&#xff0c;而且要求用的硬币数量尽可能少。 准备工作&#xff1a;首先&#xff0c;我们做了一张表&#xff08;叫dp&#xff09;&#xff0c;这张表记…
阅读更多...
前端开发的第三方库

前端开发的第三方库

base64.js 地址&#xff1a;https://github.com/dankogai/js-base64 Base64.js 库提供了一个简单的 API&#xff0c;用于将数据转换为 Base64 编码&#xff0c;以及将 Base64 编码的数据解码回原始数据 Base64.js 是一个 JavaScript 库&#xff0c;用于将数据转换为 Base64 编…
阅读更多...
LVGL：拓展部件——键盘 lv_keyboard

LVGL：拓展部件——键盘 lv_keyboard

一、概述 此控件特点&#xff1a; 特殊Button矩阵&#xff1a;lv_keyboard 本质上是一个经过定制的按钮矩阵控件。每个按钮都可以独立触发事件或响应。预定义的键映射&#xff1a;lv_keyboard 自带了一套预设的按键布局和对应的字符映射表&#xff0c;开发者可以根据需要选择…
阅读更多...
Vue 性能不给力？这些优化技巧帮你轻松搞定！

Vue 性能不给力？这些优化技巧帮你轻松搞定！

结合lighthouse查看各项数据&#xff0c;不断进行性能优化&#xff0c;可以从代码、项目打包、项目部署这三个层面来优化 代码层面 1、v-if和v-show区分使用 v-if&#xff08;惰性的&#xff09;用的条件判断&#xff0c;是惰性的&#xff0c;false的话初始不会渲染&#xf…
阅读更多...
oracle迁移至gbase，sql问题总结（完善中）

oracle迁移至gbase，sql问题总结（完善中）

最近再做国产化适配&#xff0c;需要把oracle里面的数据迁移至gbase 8a库中&#xff0c;这边把迁移过程中遇到的sql问题&#xff0c;记录下&#xff0c;现在仅迁移了一部分&#xff0c;后续会继续完善 1.ORACLE里面的NVL2函数在8a中不支持&#xff0c;可换成DECODE函数 2.表别…
阅读更多...
二鼠打洞问题

二鼠打洞问题

文章目录 二鼠打洞问题测试说明Python求解 二鼠打洞问题 《九章算术》的“盈不足篇”里有一个很有意思的老鼠打洞问题。原文是这么说的&#xff1a;今有垣厚十尺&#xff0c;两鼠对穿。大鼠日一尺&#xff0c;小鼠亦一尺。大鼠日自倍&#xff0c;小鼠日自半。问&#xff1a;何…
阅读更多...
此站点正在尝试打开 ，chrome/edge 允许http网站打开url schema

此站点正在尝试打开 ，chrome/edge 允许http网站打开url schema

正常https链接会有首次允许选项 但http没有&#xff0c;每次都会弹出&#xff0c;非常烦人。 Chrome / Edge 配置 地址栏输入 chrome://flags/搜索Insecure origins treated as secure, 配置允许网站&#xff0c;需要协议和端口再次跳转会显示始终允许选项
阅读更多...
关于5.x版本的Neo4j与py2neo的访问技巧

关于5.x版本的Neo4j与py2neo的访问技巧

先说结果。 Neo4j是可以使用py2neo来操作的。而且网上搜到的教程和方法里&#xff0c;首推的http连接方法可能并不是最好的&#xff0c;应该用 bolt 方法可能更好。 对于大多数使用 py2neo 与 Neo4j 数据库进行交互的应用程序来说&#xff0c;建议使用 Bolt 协议&#xff08;即…
阅读更多...
最新文章

Copyright @ 2022~2023