目录
1.介绍
2.使用scipy
1. 安装
2.拟合曲线
3.随机变量与概率分布
4.假设检验
5.参数检验
3.使用Scikit-Learn
1. 机器学习库,建立在numpy,scipy,matplotlib基础上
2.包含功能
3.安装
1.官网:https://scikit-learn.org
2.下载
3.线性回归模型
4.归一化
5.标准化
6.OneHot独热编码
7.非监督学习-聚类算法K-Means
8.监督学习-KNN算法
9.监督学习-回归模型-多元线性回归模型
1.介绍
1.应用库基础关系
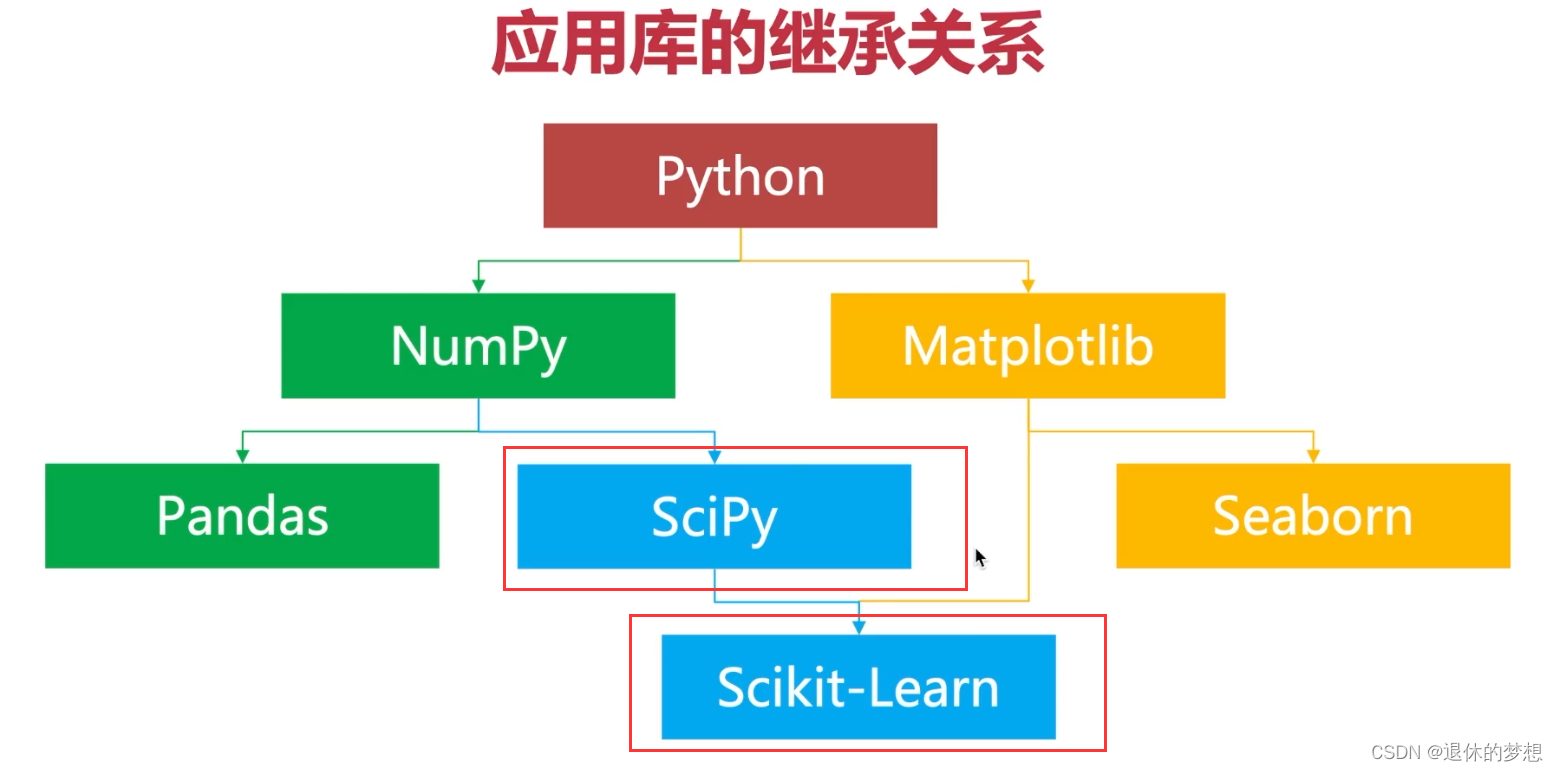
2..scipy是用于统计函数:如矩阵运算,参数优化,假设检验
3.Scikit-Learn回归算法:监督学习、分类算法、回归算法
4.Scikit-learn聚类算法:非监督学习,特征聚类分群
4.scipy官网:SciPy -
2.使用scipy
1. 安装
pip install scipy
import scipy
2.拟合曲线
# coding:utf-8import numpy as np import matplotlib.pyplot as plt import scipy.optimize# 创建e方程= a*e^(-b*x)+c def y(x, a, b, c):return a * np.exp(-b * x) + cxdata = np.linspace(0, 4, 50) ydata = y(xdata, 2.5, 1.3, 0.5) ydata_noise = ydata + 0.5 * np.random.randn(xdata.size) print(xdata) print(ydata)plt.plot(xdata, ydata_noise) # 生成拟合曲线 params, pcov = scipy.optimize.curve_fit(y, xdata, ydata) plt.plot(xdata,y(xdata,*params))plt.show()
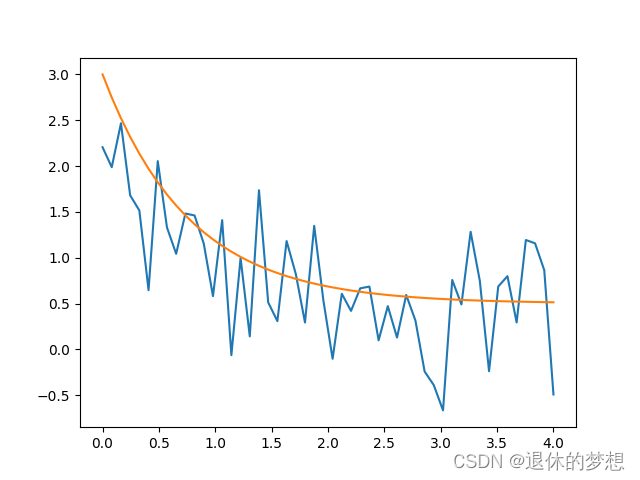
3.随机变量与概率分布
1. 统计学的应用价值
- 应用数学的一个分支
- 利用概率论建立数学模型,收集所2观察系统的数据
- 进行量化分析,总结,进而进行推断和预测
- 为相关决策提供依据和参考
2.什么是随机变量
- 观察数据样本:1.具有不确定性和随机性 2.落在某一个范围的概率是一定的
3.什么是概率分布
- 随机变量取值的概率:某件事的概率,就是这件事在当前样本或者说实验中出现的次数,出现的可能性的意思
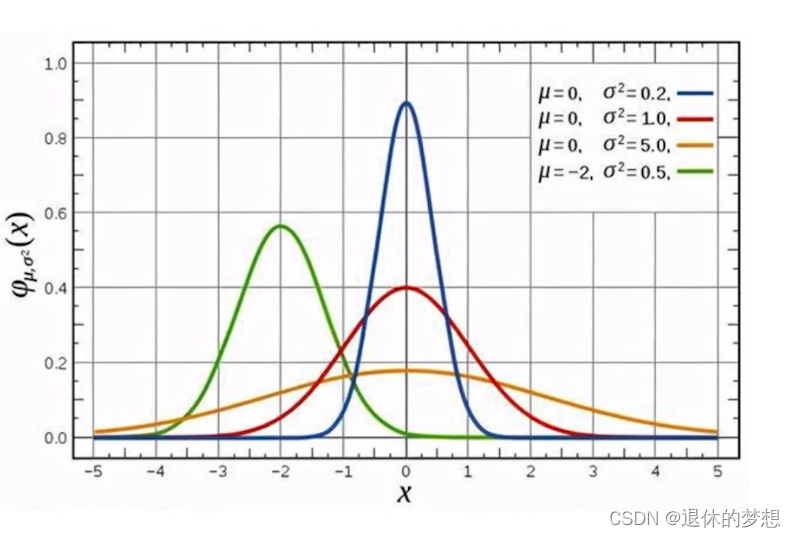
4.概率分布值正态分布:
一般为中间高2边低成为正态分布,可以确立正常的取值范围

# coding:utf-8import numpy as np import matplotlib.pyplot as plt import scipy.stats as st import seaborn as sns#创建随机变量,设置size,设置loc期望值,设置scale方差 rvs1=st.norm.rvs(0,1,100)#改的方差缓存变化 rvs2=st.norm.rvs(0,2,100) rvs3=st.norm.rvs(0,3,100)#绘制分布图 for i in [rvs1,rvs2,rvs3]:sns.distplot(i) #设置lable plt.legend(labels=["1","2","3"])plt.show()

4.假设检验
1.什么是统计推断
- 通过样本推断总体的一种统计方法
- 通过概率分布的数量特征(如期望和方差)来反映22
- 对总体的位置参数进行估计
- 对于参数的假设进行检查
- 对总体进行预测预报等
2.什么是假设检验
- 判断样本与样本、样本与总体的差异
- 是由”抽样误差”引起的还是“本质差别”照成的统计推断方法
如:

3.显著性检验
- 通过对总体的特征,做出某种假设,并进行抽样研究的统计推理方法
- 最终基于出现概率的大小,并判断接受或者拒绝某种假设
如:

# coding:utf-8import numpy as np import matplotlib.pyplot as plt import scipy.stats as st import seaborn as sns import matplotlib as mplmpl.rcParams["font.family"] = "FangSong" # 设置字体 mpl.rcParams["axes.unicode_minus"] = False # 正常显示负号#设置样本的概率分布 #整体样本 mean0=72 #有效样本数量 mean1=68 #方差0.8 std1=0.8 rvs0=st.norm.rvs(mean0,1,1000) rvs1=st.norm.rvs(mean1,std1,1000)for i in [rvs0,rvs1]:sns.distplot(i)#置信区间:总体概率为95%#设置lable plt.legend(labels=["72样本","68样本"])plt.show()

5.参数检验

1.置信区间:总体概率为95%
2.样本差异性比较:stats.ks_2samp(样本1,样本2,"类型")
3.使用Scikit-Learn
1. 机器学习库,建立在numpy,scipy,matplotlib基础上

2.包含功能
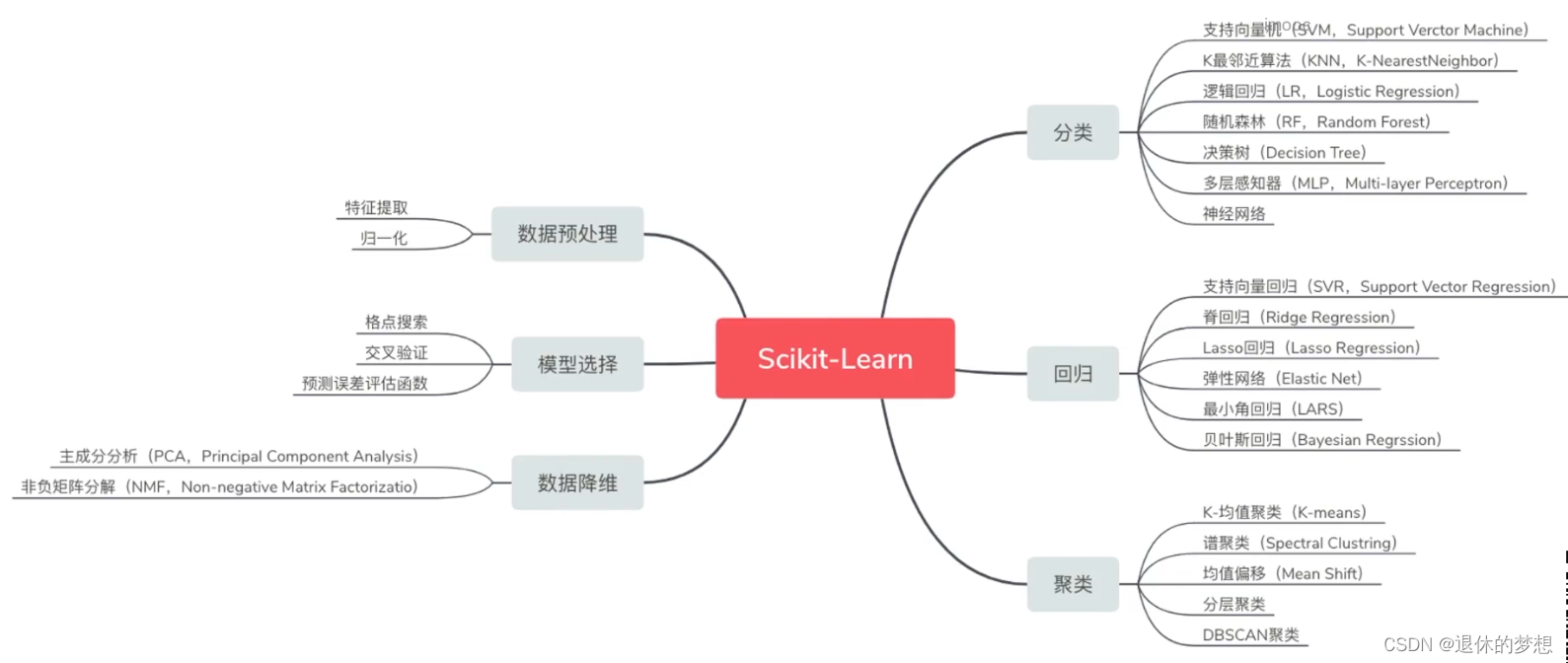
3.安装
1.官网:https://scikit-learn.org
2.下载
pip install scikit-learn
3.线性回归模型
# coding:utf-8import pandas as pd
import numpy as np
import sklearn as sk
from sklearn import datasets
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt# 导入波士顿房价数据
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep=r"\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
# 人口中地位较低的百分比
target = raw_df.values[1::2, 2]
# print("data=====",data)
print("target======", target)
# 样本数据
# print(data.shape)house = pd.DataFrame(data)
house.columns = ["城市的人均犯罪率", " 25,000英尺以上的住房占的比例", "每个城镇的非零售商业英亩的比例", "如果靠近河岸","环保指数", "每个住宅的平均房间数", "自住比例", "就业中心距离","到公路的可达指数", "物业税", "学生教师比例", "黑人比例", "人口中地位较低的百分比"]
print(house)
# 使用回归线性模型 y=w*x +bmod = LinearRegression() # 确定要调用的模型
x = data[:, np.newaxis, 5] # 房间数
y = target #
mod.fit(x, y)
# 相关性指数 0-1
print("相关性指数:", mod.score(x, y))
print("回归系数coef_:", mod.coef_)
print("回归系数intercept_:", mod.intercept_)# 绘制样本
plt.scatter(x, y)
plt.plot(x, mod.predict(x), color="red")plt.show()
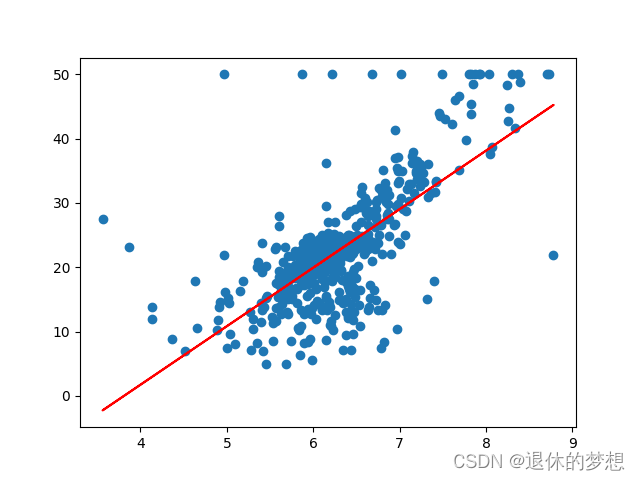
4.归一化
1.数据归一化的作用是为了降低数据差异,将数据的取值范围设置在0-1
# coding:utf-8import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib as mpl
import sklearn as sk
import matplotlib.pyplot as plt
from sklearn import preprocessing as prepmpl.rcParams["font.family"] = "FangSong" # 设置字体
mpl.rcParams["axes.unicode_minus"] = False # 正常显示负号fig, ax = plt.subplots(2, 2)
# 创建随机样本
data = pd.DataFrame({"a": np.random.exponential(3, 1000), # a数据为 3的方差,生成1000个数字"b": np.random.normal(-5, 0.5, 1000), # b数据为以-5位中心,0.5的方差,生成1000个数字"c": np.random.normal(0, 4, 1000) # 以0位为中心,4的方差,生成1000个数字
})
print("数据样本:", data.describe())
# 原始数据 则线图
sns.lineplot(data, ax=ax[0, 0])
ax[0, 0].set_title("原始数据-折线图")# 分布图
sns.distplot(data["a"], ax=ax[0, 1])
sns.distplot(data["b"], ax=ax[0, 1])
sns.distplot(data["c"], ax=ax[0, 1])
ax[0, 1].set_title("原始数据-分布图")# 数据归一化的作用是为了降低数据差异,将数据的取值范围设置在0-1
# 归一化模型 算法:X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
scaler1 = prep.MinMaxScaler()
scaler1.fit(data)minMax1 = pd.DataFrame(scaler1.transform(data), columns=["a", "b", "c"])sns.lineplot(data=minMax1, ax=ax[1, 0])
ax[1, 0].set_title("归一化-折线图")sns.distplot(minMax1["a"], ax=ax[1, 1])
sns.distplot(minMax1["b"], ax=ax[1, 1])
sns.distplot(minMax1["c"], ax=ax[1, 1])
ax[1, 1].set_title("归一化-分布图")# 设置间距,避免名称重叠
fig.tight_layout()plt.show()

5.标准化
数据标准化, 将数据转换为0为均值,1位方差
# coding:utf-8import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib as mpl
import sklearn as sk
import matplotlib.pyplot as plt
from sklearn import preprocessing as prepmpl.rcParams["font.family"] = "FangSong" # 设置字体
mpl.rcParams["axes.unicode_minus"] = False # 正常显示负号fig, ax = plt.subplots(2, 2)
# 创建随机样本
data = pd.DataFrame({"a": np.random.exponential(3, 1000), # a数据为 3的方差,生成1000个数字"b": np.random.normal(-5, 0.5, 1000), # b数据为以-5位中心,0.5的方差,生成1000个数字"c": np.random.normal(0, 4, 1000) # 以0位为中心,4的方差,生成1000个数字
})
print("数据样本:", data.describe())
# 原始数据 则线图
sns.lineplot(data, ax=ax[0, 0])
ax[0, 0].set_title("原始数据-折线图")# 分布图
sns.distplot(data["a"], ax=ax[0, 1])
sns.distplot(data["b"], ax=ax[0, 1])
sns.distplot(data["c"], ax=ax[0, 1])
ax[0, 1].set_title("原始数据-分布图")# 数据标准化, 将数据转换为0为均值,1位方差
scaler1 = prep.StandardScaler()
scaler1.fit(data)minMax1 = pd.DataFrame(scaler1.transform(data), columns=["a", "b", "c"])sns.lineplot(data=minMax1, ax=ax[1, 0])
ax[1, 0].set_title("标准化-折线图")sns.distplot(minMax1["a"], ax=ax[1, 1])
sns.distplot(minMax1["b"], ax=ax[1, 1])
sns.distplot(minMax1["c"], ax=ax[1, 1])
ax[1, 1].set_title("标准化-分布图")# 设置间距,避免名称重叠
fig.tight_layout()plt.show()
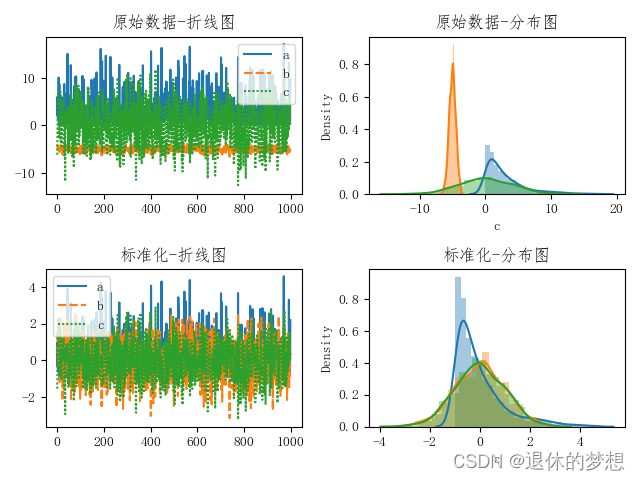
6.OneHot独热编码
1. 自然编码vs独热编码
独热编码是以0和1表示的,将特定类特征的转换为二进制
比如:性别:男、女 以编码标识为 1,0 独热编码为 男:[1,0] 女[0,1]
再比如:胜平负 1胜利 2平 3负 独热编码为 胜:[1,0,0] 平:[0,1,0] 负:[0,0,1]
from sklearn import preprocessing as prep import pandas as pdsex = ["f", "m"] spf = ["s", "p"] zhiffs = ["x", "z"]df = pd.DataFrame([sex,spf,zhiffs]) # 创建模型》fit训练数据》transform显示数据》.attribute打印数据 oneHot = prep.OneHotEncoder(sparse_output=False,handle_unknown='ignore') oneHot.fit(df) print(oneHot.transform([["f","m"]]))
out:
[[1. 0. 0. 1. 0. 0.]]
7.非监督学习-聚类算法K-Means

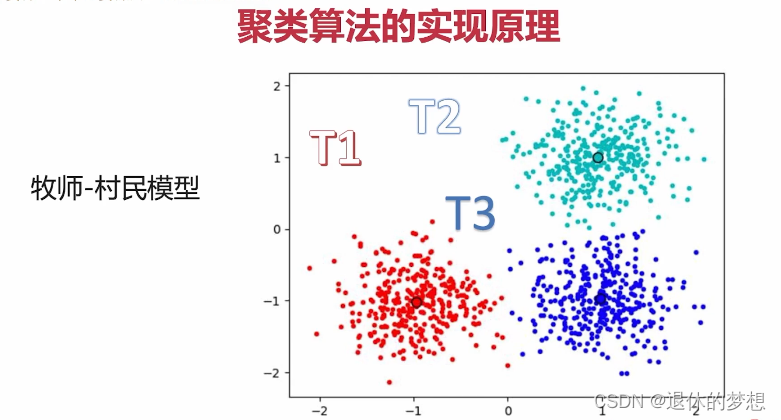

8.监督学习-KNN算法


9.监督学习-回归模型-多元线性回归模型
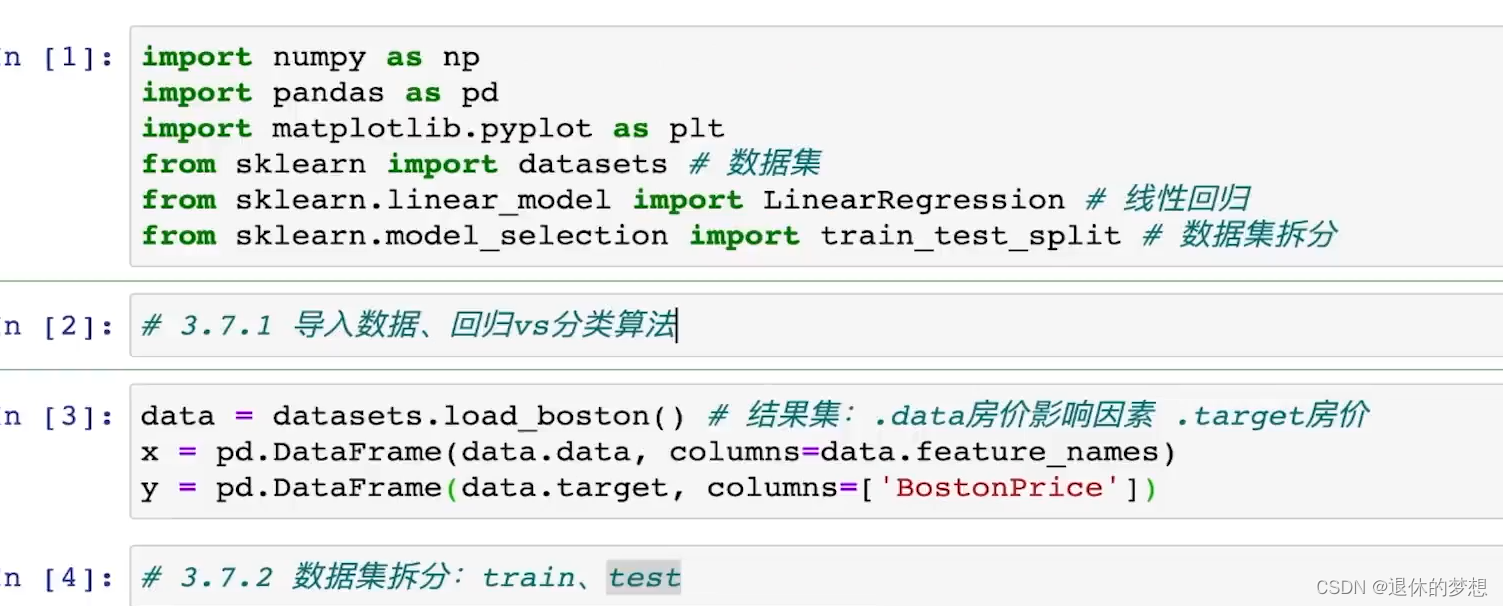
(二))


(关系模型))


之远程命令)




 快速入门)



)



:智慧城市、智慧工厂、智慧建筑、智慧校园。。。)