Catmull-Rom P5 ThreeJs与前端

文章目录

- 问题
- - Echarts 3D如何让曲线变得平滑？
  - Echarts 2D图中平滑效果是如何实现的？
  - 如何在一个Echarts 3D图中画一个圆圈？
  - 如何在Echarts 3D图中画一个立方体？
- Catmull-Rom插值算法
- - 先来回答第二个问题
  - 回到第一个问题
  - 在Echarts 3D图中画一个圆圈
  - 在Echarts 3D图中画一个立方体

问题

Echarts 3D如何让曲线变得平滑？

假设，你遇到了如下需求：
将如下数据，在Echarts 3D图中展示出来

lineData: [[0, 30, 5],[10, 20, 10],[20, 50, 13],[30, 15, 25],[40, 20, 33],[50, 33, 50],[60, 24, 66],[70, 10, 80],[80, 28, 90],],

这个需求很常规，最终呈现的效果是这样的：
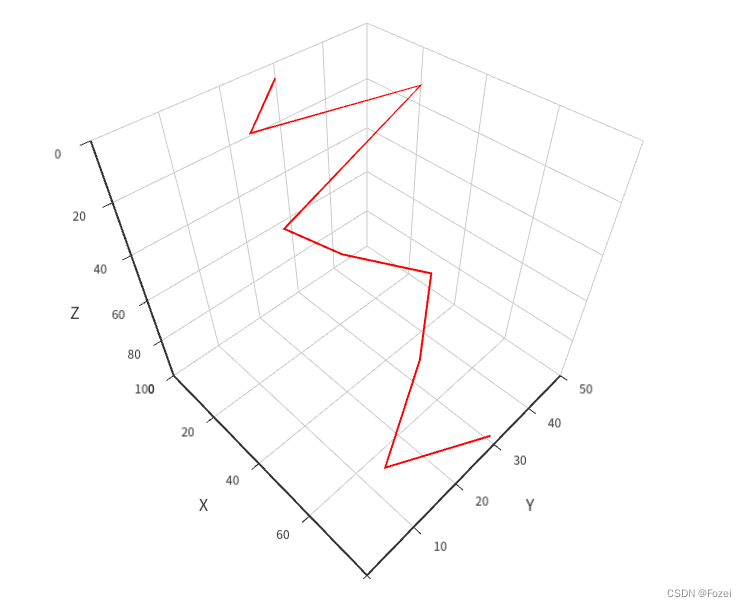
请添加图片描述
可以看到，在Echarts 3D图中，line3D模式下，上述数据集的成图效果是折线。现在再变更一个需求：要求折线数据端点处的过渡要平滑。
于是，我们立刻想到了Echarts 2D图中series中是可以配置smooth: true,这个属性的，通过这个属性，可以让折线在Echarts 2D图上的过渡变得平滑。然而很遗憾，当你在Echarts 3D图中进行上述设置时，并没有任何效果。

Echarts 2D图中平滑效果是如何实现的？

再比如，上述数据集，只取每个元素的前两个数据，不做平滑处理，它在Echarts 2D图上成图效果是这样的：
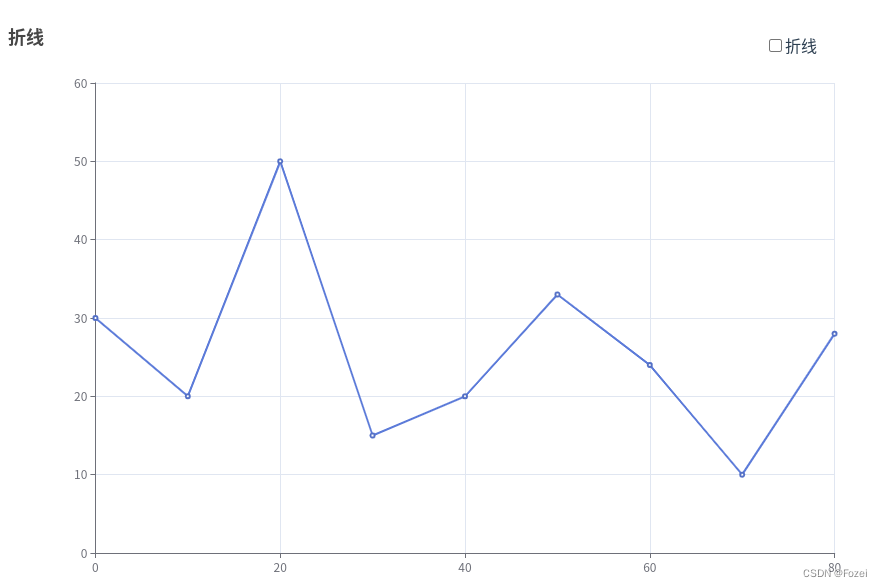
请添加图片描述
开启数据平滑之后，它的成图效果是这样的：

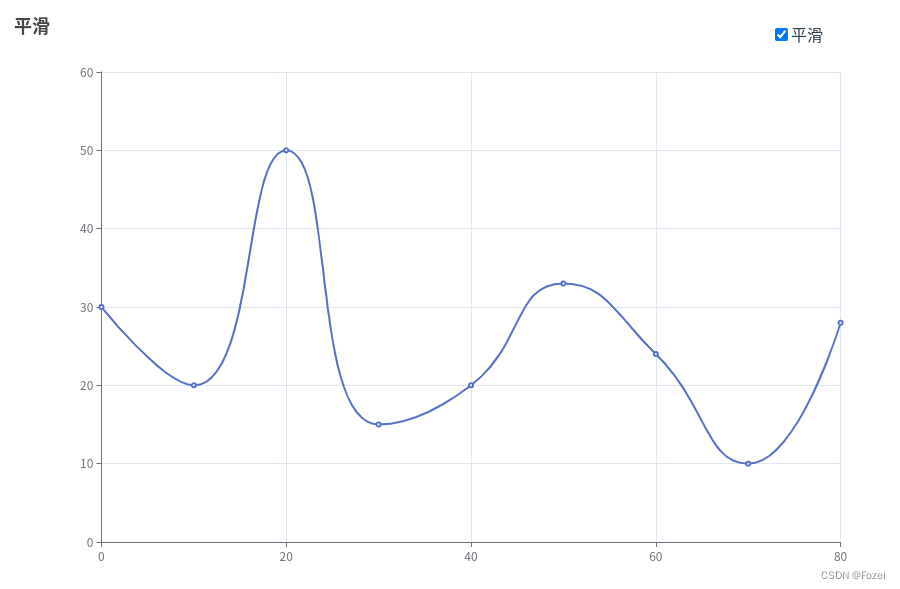
那么，Echarts 2D图中的平滑效果，是如何实现的？

如何在一个Echarts 3D图中画一个圆圈？

如何在Echarts 3D图中画一个立方体？

Catmull-Rom插值算法

先来回答第二个问题

实际上，在Echarts 2D图中，使用的是Catmull-Rom插值算法，它的绘图规则，是每个点 ( P_i ) 的切线方向等于其相邻两个控制点 ( P_{i-1} ) 和 ( P_{i+1} ) 连线的方向。下图为了说明Catmull-Rom插值算法的绘图规则，使用P5js curve方法，绘制的一个有两个控制点c1和c2经过平面上p1和p2的曲线。而P5js curve方法的底层，就是使用的Catmull-Rom插值算法。但是P5js对这个方法的文档描述可能有点问题，后半部分参数对照有问题，参数的意义应该分别是控制点、途经点、途经点和控制点。
P25 Curve

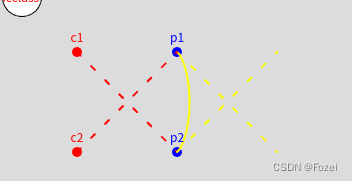
在这里插入图片描述
回到Echarts 2D图中平滑曲线的实现，为了证明Echarts 2D图中使用的是Catmull-Rom插值算法，我们把smooth:true的配置去掉，然后使用ThreeJs中的SplineCurve构建曲线（SplineCurve使用的是Catmull-Rom插值算法），然后通过增加细分数（也就是调用getPoints(pointCount)方法时，增加pointCount的值），进行验证。

在这里插入图片描述
SplineCurve

const v2Array = this.lineData.map((value) => {return new THREE.Vector2(value[0], value[1]);});
const curve = new THREE.SplineCurve(v2Array);
const points = curve.getPoints(this.pointsCount);
// series
series: [{type: "line",data: points.map((point) => {return [point.x, point.y];}),},
],

在这里插入图片描述
可以看到，当细分数增加时，同样的数据集，最终和Echarts 2D图中平滑曲线的效果是一致的。

回到第一个问题

通过Catmull-Rom插值算法，可以进行二维空间曲线的平滑效果，同样的，在三维空间中，也是可以进行运算的。ThreeJs的CatmullRomCurve3这个曲线，就是进行空间曲线Catmull-Rom插值的对象。

 // 把关键点，变成三维Vector
const keyPoints = this.lineData.map((point) => {
return new THREE.Vector3(point[0], point[1], point[2]);
});
// 根据关键点，生成贝塞尔曲线
const curve = new THREE.CatmullRomCurve3(keyPoints);
// 构建series
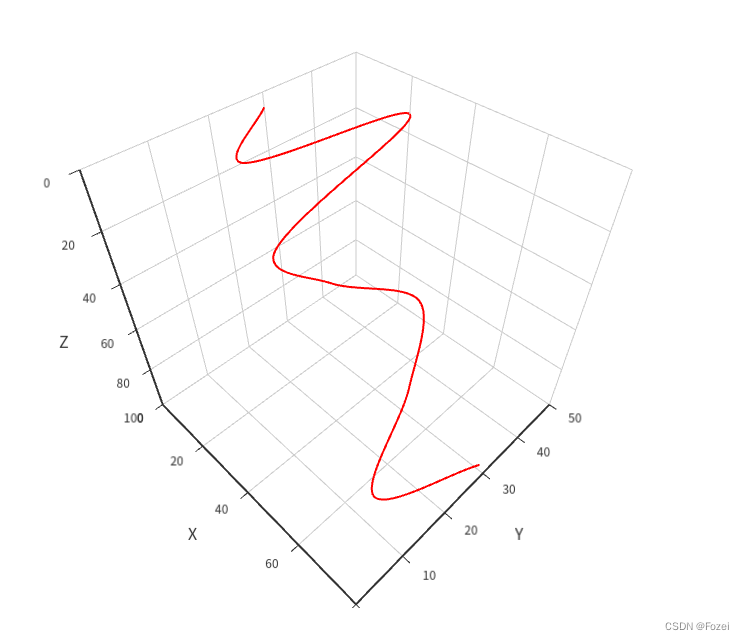
series: [{type: "line3D",data: curve.getPoints(300).map((point) => {return [point.x, point.y, point.z];}),lineStyle: {width: 2,color: "red",},},
],

最终呈现的三维空间平滑曲线效果：
在这里插入图片描述

在Echarts 3D图中画一个圆圈

在Echarts 2D图中，我们通过自定义序列和graphic等API，是可以绘制基本几何图形的，然而，在Echarts 3D图中，却没有这个概念。
那么，要想在Echarts 3D图中画出一个圆，我们通过ThreeJs构建一个圆形，然后获取这个圆形每个点的坐标，最终通过line3D的方式，来画出一个圆：

const curve = new THREE.EllipseCurve(40,40, // ax, aY20,20 // xRadius, yRadius);
const points = curve.getPoints(50);
// 构建series
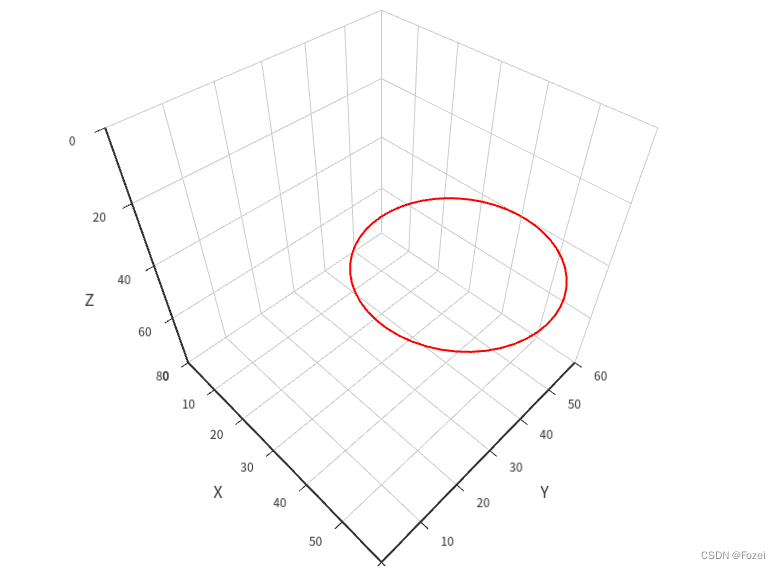
series: [{type: "line3D",data: points.map((point) => {return [point.x, point.y, 40];}),lineStyle: {width: 2,color: "red",},},
],

效果：
在这里插入图片描述
EllipseCurve
注意：这种方法呈现的圆形曲线，是平行与xy平面的，由于Curve没有旋转API的，所以如果需要其他朝向的圆，需要使用其他方式。

在Echarts 3D图中画一个立方体

立方体在3d图中的绘制，如果基础数据齐全（比如知道8个顶点的位置关系），还是比较简单的；但是如果信息有限，8个点的数据，需要间接计算出来（比如只知道几何体几何中心的位置和长宽高，或者需要进行平移，旋转等操作），那就比较繁琐了。Echarts 3D图中，使用ThreeJs，能帮助我们绕开这些繁琐的计算。

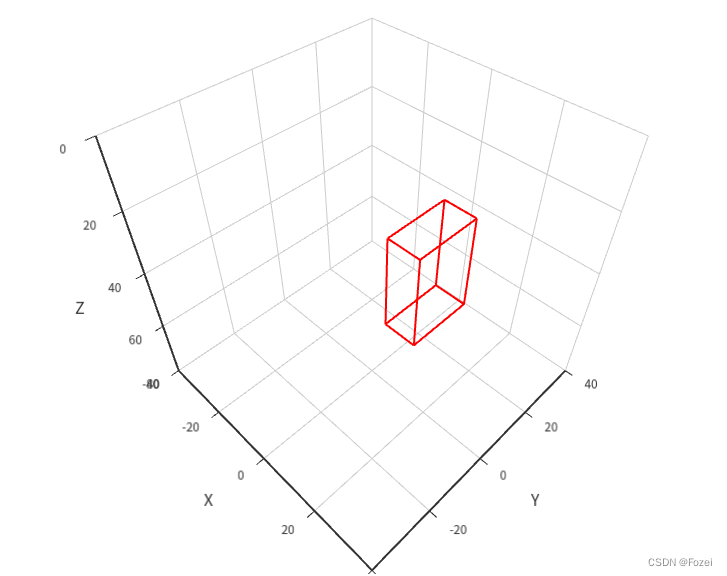
 const geometry = new THREE.BoxGeometry(10, 20, 30);geometry.translate(10, 10, 40);//   边信息const linePoints = [];const edges = new THREE.EdgesGeometry(geometry);const lineSegments = new THREE.LineSegments(edges);const lineGeometry = lineSegments.geometry;const xyzValues = lineGeometry.attributes.position.array;const valuesPerLine = 6;for (let i = 0; i < xyzValues.length; i += valuesPerLine) {const chunk = xyzValues.slice(i, i + valuesPerLine);linePoints.push([chunk.slice(0, 3), chunk.slice(3, 6)]);}// 构建series
series: linePoints.map((pointArray) => {return {type: "line3D",data: pointArray.map((point) => {return [point[0], point[1], point[2]];}),lineStyle: {width: 2,color: "red",},};
}),

效果：

在这里插入图片描述