一、问题提出
(一)要求
1.随机生成>=10万个三维点的点云,并以适当方式存储
2.自行实现一个KNN算法,对任意Query点,返回最邻近的K个点
3.不允许使用第三方库(e.g.flann,PCL,opencv)!
4.语言任选(推荐C++或者Python)
(二)规则
1.正确实现(3')
2.优于Flann、PCL在相同输入下的KNN求解函数中的一种(2')
3.优于Flann、PCL在相同输入下的KNN求解函数中的两种(2')
4.创新性评估(3')
二、KNN算法概述
KNN(K-Nearest Neighbor)算法,也称为K最邻近法,是一种基本的机器学习算法,属于有监督学习中的分类算法。该算法最初由Cover和Hart于1968年提出,具有简单直观的特点。
KNN算法的思路是:如果一个样本在特征空间中的K个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。这里的K通常是一个用户指定的整数,通常选取奇数以避免出现平局的情况。
KNN算法的距离度量通常是欧氏距离,但也可以使用其他距离度量方法。在选择K值时,较小的K值可能会使算法对噪声更加敏感,而较大的K值可能会使算法分类边界变得模糊。因此,选择合适的K值对于KNN算法的性能至关重要。
三、算法描述
(一)语言选择
所选语言为MATLAB,软件版本为MATLAB R2022a
(二)算法原理
K近邻算法,即是给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例,这K个实例的多数属于某个类,就把该输入实例分类到这个类中。(这就类似于现实生活中少数服从多数的思想),也就是在训练数据集中寻找与待预测样本A距离最近的K个样本,如果K个样本中大多数属于类别甲,少数属于类别乙,那个就可以认为样本A属于类别甲。
(三)距离度量
一般计算样本在多维空间的距离有两种方式:欧式距离和曼哈顿距离。
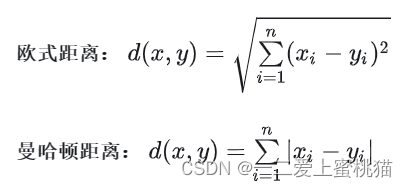
在实际KNN问题应用中,距离函数的选择应该根据数据的特性和分析的需要而定,选择欧式距离表示。
(四)算法流程
1.设置样本点数量,此处定义N为样本点数目的一半。
2.设置矩阵label1、label2存储样本点所属类别,label1为第一类,label2位第二类。
3.生成随机数矩阵data1、data2。为了使样本点更具分散性,此处选择直接使用rand函数,而不是正态随机数randn和mvnrnd函数。
4.利用三维绘图函数scatter3绘制两类样本点,如下图所示(此处使用N=100举例,增加可视性):
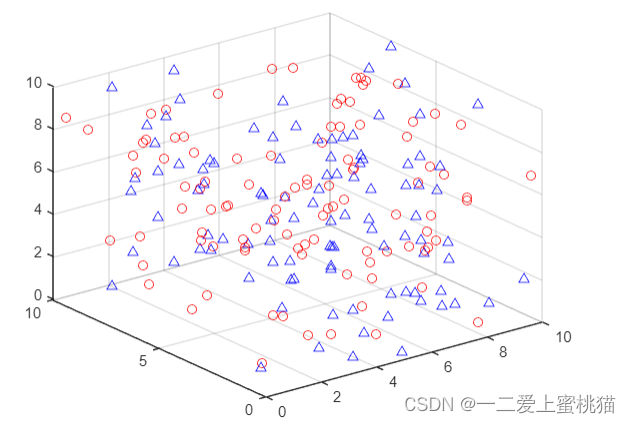
其中,红色代表第一类样本点,蓝色代表第二类样本点。
- 设置K值为11(K必为奇数),即周围11个样本点。
- 遍历从(3,3,3)至(7,7,7)范围内的125个点,间隔为1个单位。
7.计算待预测样本与训练数据集中样本特征之间的欧式距离dis。
8.按照距离递增的顺序,使用sort函数排序,返回排序后的矩阵B及其索引值矩阵index。
9.选取距离最近的K个样本以及所属类别的次数,输出最近的K个样本坐标(见附件:最邻近K点输出结果.xlsx)。
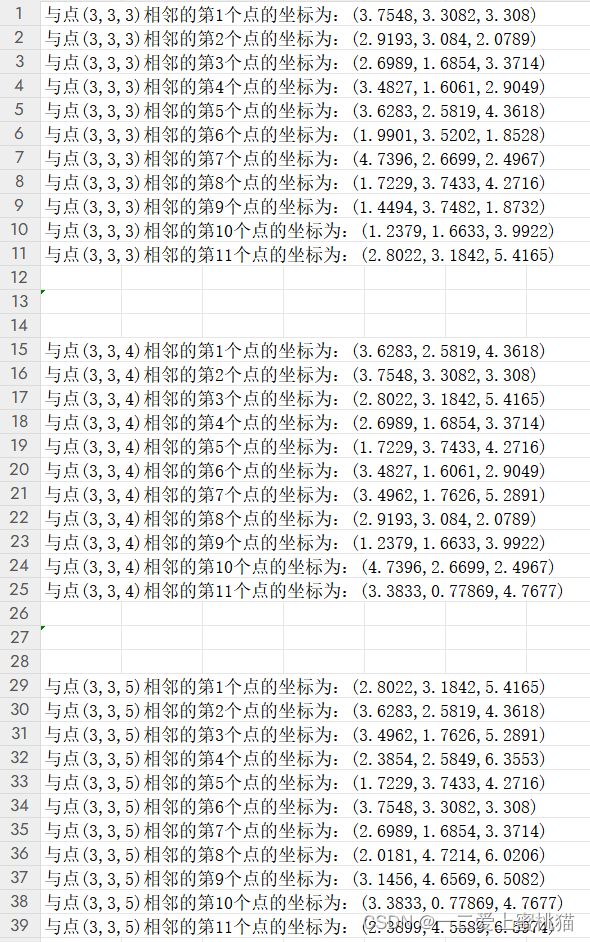
10.分别用变量c1、c2存储出现的类别次数,返回前k个点所出现频率最高的类别作为预测分类结果。
11.数据可视化处理,如下图所示(N为100时):
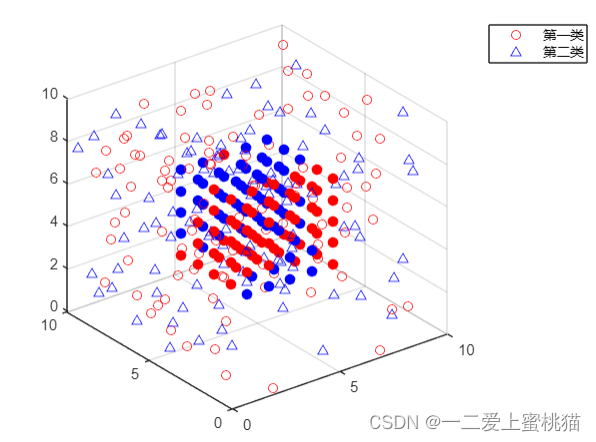
当n=50000时(即分析10万个样本点时),图像如下图所示:
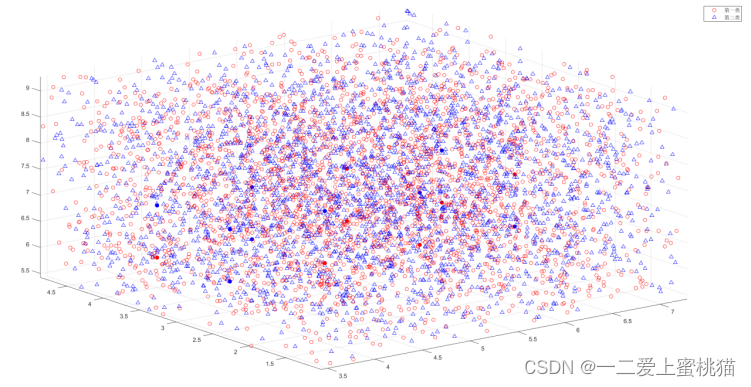
四、代码实现
% KNN算法
clear all;
clc;
%总体样本点数量为2N
N=50000;
% 每一个数据有两个特征
label1 = ones(N,1);%第一类点云序号,记为1
label2 = 1+ones(N,1);%第二类点云序号,记为2
%生成第一类数据
data1 = 10*rand(N,3);%坐标范围为[0,10]
data1(data1<0)=0;
%生成第二类数据
data2 = 10*rand(N,3);
data2(data1<0)=0;
scatter3(data1(:,1),data1(:,2),data1(:,3),'ro')%红色圆圈代表第一类数据
hold on;
scatter3(data2(:,1),data2(:,2),data2(:,3),'b^')%蓝色三角代表第二类数据
hold on;
data = [data1;data2];%两类数据整合,放在一个矩阵里
label = [label1;label2];%两类数据类别序号整合,也放在一个矩阵里
K= 11;%K值为11,表示周围最近的11个点。K为奇数
for i1 = 3:7for i2 = 3:7for i3=3:7testdata = [i1 i2 i3];distance=zeros(2*N,1);dis = sum((data-testdata).^2,2);%返回包含每一行总和的列向量[B index]= sort(dis);%返回索引值indexfor j=1:Kdisp("与点("+num2str(i1)+","+num2str(i2)+","+num2str(i3)+")相邻的第"+num2str(j)+"个点的坐标为:("+num2str(data(index(j,1),1))+","+num2str(data(index(j,1),2))+","+num2str(data(index(j,1),3))+")");enddisp(' ');%换行newLabel = label(index(1:K));c1 = 0;c2 = 0;for ii = 1:Kif newLabel(ii)==1c1 = c1+1;%第一类的点数量加一elsec2 = c2+1;%第二类的点数量加一endendif c1>c2%第一类的数量的点更多scatter3(testdata(1),testdata(2),testdata(3),50,'ro','filled')else%第二类的数量的点更多scatter3(testdata(1),testdata(2),testdata(3),50,'bo','filled')endendend
end
legend('第一类','第二类')
整体过程偏向于暴力,仅供参考


)







:环境配置)








 复用和信道编码(一))