PCA+DBO+K-means聚类，蜣螂优化算法DBO优化K-means，适合学习，也适合发paper。

一、 蜣螂优化算法

摘要：受蜣螂滚球、跳舞、觅食、偷窃和繁殖等行为的启发，提出了一种新的基于种群的优化算法(Dung Beetle Optimizer, DBO)。新提出的DBO算法兼顾了全局探索和局部开发，具有收敛速度快和求解精度高的特点。采用一系列著名的数学测试函数(包括23个基准函数和29个CEC-BC-2017测试函数)来评估DBO算法的搜索能力。仿真实验结果表明，DBO算法在收敛速度、求解精度和稳定性方面均表现出与当前主流优化算法相当的性能。此外，采用Wilcoxon符号秩检验和Friedman检验对算法的实验结果进行评估，证明了DBO算法相对于当前流行的其他优化技术的优越性。为了进一步说明DBO算法的实际应用潜力，将DBO算法成功应用于3个工程设计问题。实验结果表明，所提DBO算法能够有效地处理实际应用问题。

文献来源：Dung beetle optimizer: a new meta-heuristic algorithm for global optimization。

DOI：10.1007/s11227-022-04959-6。

二、K-means聚类

K-means聚类算法是一种无监督学习算法，广泛应用于数据分析和机器学习的各个领域。其核心思想是将给定的样本集划分为K个簇，使得每个簇内的样本点尽可能紧密地聚集在一起，而不同簇之间的样本点则尽可能远离。以下是K-means聚类算法的主要优点：

简单直观：K-means算法原理简单易懂，容易实现，计算速度快，且聚类效果通常较好。

可解释性强：算法的结果具有明确的解释性，每个簇的中心点可以代表该簇的特征，有助于理解和分析数据。

适用于大规模数据集：K-means算法在处理大规模数据集时表现良好，能够高效地划分数据。

然而，K-means聚类算法也存在一些明显的缺点：

K值选择困难：K值是事先给定的，如何选择合适的K值是一个难题。K值选择不当可能导致聚类结果不合理，难以反映数据的真实结构。

对初始值敏感：K-means算法对初始簇中心的选择非常敏感。如果初始值选择得不好，可能会导致算法陷入局部最优解，而无法得到全局最优的聚类结果。

对异常值和噪声敏感：K-means算法对异常值和噪声的鲁棒性较差，这些值可能会影响簇中心的计算，导致聚类结果不准确。

不适合非凸形状簇：K-means算法基于距离度量进行聚类，因此对于非凸形状的簇可能无法得到理想的聚类效果。

距离度量方式选择：关于K-means聚类算法的距离度量方式，最常用的是欧氏距离。然而，除了欧氏距离外，K-means算法也可以使用其他距离度量方式，例如曼哈顿距离和马氏距离等。

三、主成分分析PCA

主成分分析（Principal Component Analysis），是一种常用的数据降维方法。它的主要思想是通过线性变换将原始的高维数据映射到一个低维空间中，同时尽可能地保留原始数据的主要特征信息。

具体来说，PCA降维的过程可以分为以下几个步骤：

数据标准化：首先，对原始数据进行标准化处理，消除不同特征之间的量纲差异，使得每个特征都具有相同的权重。

计算协方差矩阵：接着，计算标准化后数据的协方差矩阵。协方差矩阵反映了不同特征之间的相关性，是PCA降维的关键。

计算特征值和特征向量：对协方差矩阵进行特征分解，得到特征值和特征向量。特征值的大小代表了对应特征向量方向上的数据方差，即数据的离散程度。

选择主成分：根据特征值的大小，选择前k个最大的特征值对应的特征向量作为主成分。这些主成分代表了数据中的主要变化方向，能够最大程度地保留原始数据的信息。

数据投影：最后，将原始数据投影到选定的主成分上，得到降维后的数据。这个过程可以通过将原始数据乘以主成分矩阵来实现。

PCA降维的优点在于它简单易懂，计算效率高，且能够有效地降低数据的维度，减少计算复杂性和存储空间。同时，PCA降维还能够去除部分噪声和冗余特征，提高数据的可解释性和可视化效果。因此，PCA降维在数据分析、机器学习、图像处理等领域都有广泛的应用。需要注意的是，PCA降维是一种无监督学习方法，它并不考虑数据的标签信息。因此，在某些情况下，PCA降维可能会丢失一些与标签相关的信息。此外，PCA降维对于非线性数据的处理能力有限，对于复杂的数据结构可能需要采用其他降维方法。

四、PCA+DBO+ K-means聚类

✨ 核心亮点 ✨

降维至精华：我们首先使用PCA将复杂的数据集降维到2维，保留了数据的主要信息，使其可视化变得简单直观。

优化聚类：接着，采用蜣螂优化算法DBO对K-means聚类进行优化，利用轮廓系数信息构建目标函数，自动寻找最佳的聚类数量和距离度量，以达到最优的数据分组效果。

聚类数量k：可以修改聚类数量优化范围

选择三个距离度量进行优化：sqeuclidean（欧氏距离平方）、cityblock（Block距离，也叫绝对值距离）、cosine（夹角余弦）。

代码详细中文注释，高效管理，可读性和二次开发都很好，部分代码如下： 

clc; clear; close all;% 加载Excel数据
data = xlsread('数据.xlsx');% 假设全部列为特征数据
X = data;% 数据标准化
X_standardized = (X - mean(X)) ./ std(X);% 应用PCA进行降维
[coeff, score, latent, tsquared, explained] = pca(X_standardized);% 提取前两个主成分
Z = score(:, 1:2);% 初始化DBO参数
N = 10; % 种群数量
T = 50; % 最大迭代次数
LB=[2,1]; % 变量下界
UB=[20,3]; % 变量上界
nvars=length(LB);
fobj=@fitness;% 使用DBO优化算法优化K-means进行聚类，优化最佳聚类数和最佳距离度量
[fMin,index,Convergence_curve,pos]=DBO(N,T,LB,UB,nvars,fobj,data,Z); % 计算轮廓系数
sc_xishu = mean(silhouette(data, index'));% 确定独特的聚类数
a = unique(index);
op_cluster_num = length(a); % 优化后聚类个数
C = cell(1, length(a));% 将数据分配到对应聚类
for i = 1:length(a)C(1, i) = {find(index == a(i))};
end% 分类标签
legend_str = strsplit('类别1,类别2,类别3', ',');% 绘制每个聚类的数据点
for i = 1:op_cluster_numdata_cluster = Z(C{1, i}, :);plot(data_cluster(:, 1), data_cluster(:, 2), 'p', 'LineWidth', 2, 'MarkerSize', 5); hold on;
end% 确保图例中聚类标签的数量与实际相符
if(length(legend_str) < op_cluster_num)for i = length(legend_str):op_cluster_numlegend_str{1, i} = ['类别', num2str(i)];end
end% 设置图表属性
set(gca, 'FontSize', 12)
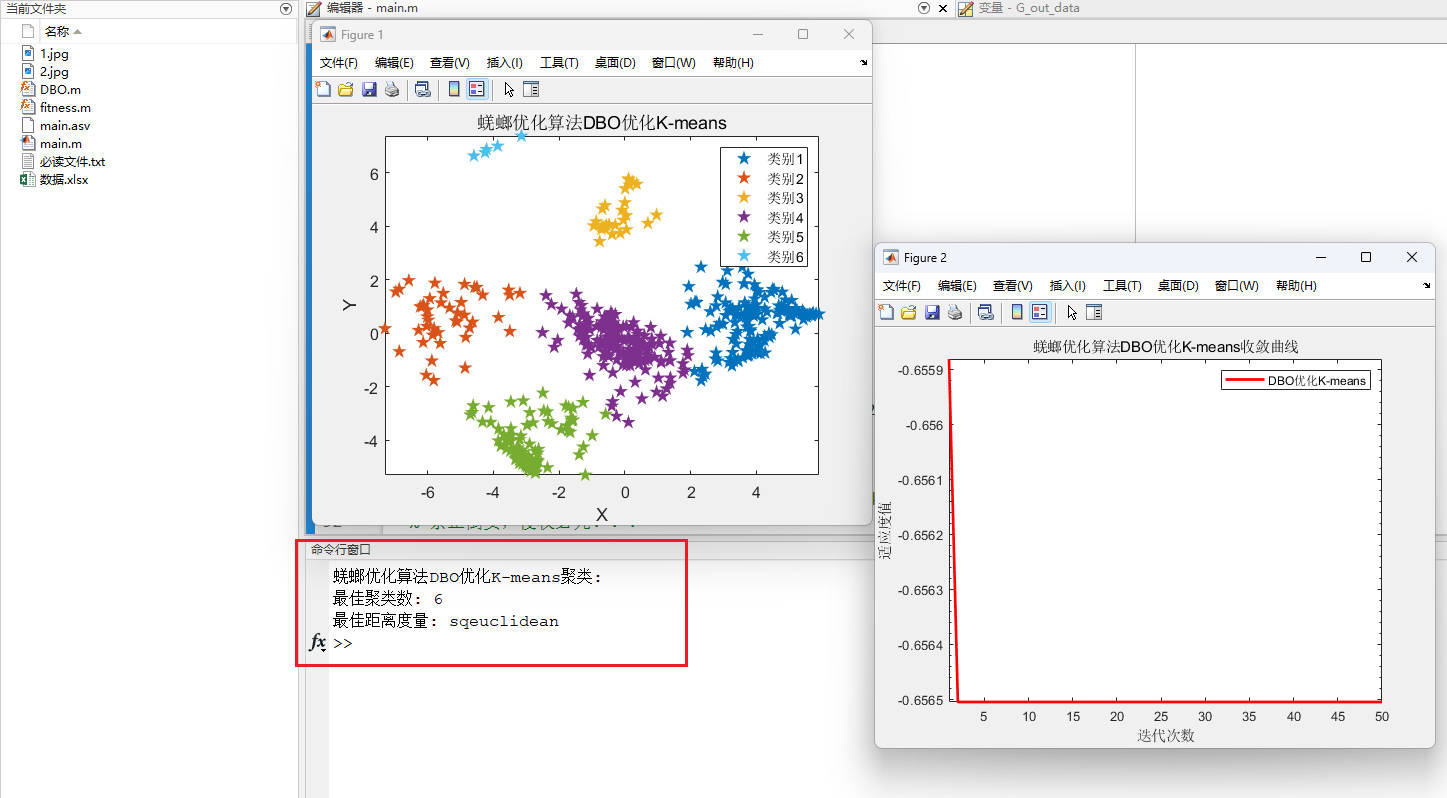
title('蜣螂优化算法DBO优化K-means')
axis tight
box on
xlabel('X')
ylabel('Y')
legend(legend_str)figure(2)
% 绘制收敛曲线
semilogy(Convergence_curve,'-r','LineWidth',2)
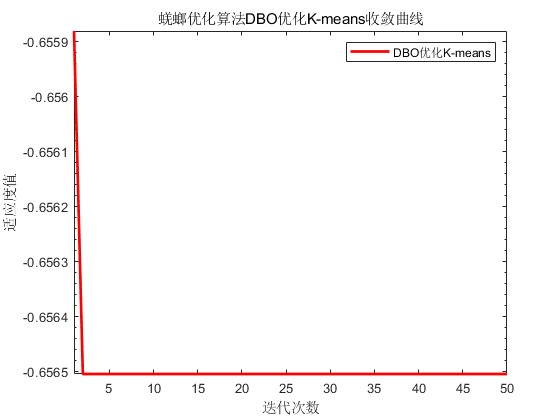
title('蜣螂优化算法DBO优化K-means收敛曲线')
xlabel('迭代次数');
ylabel('适应度值');
axis tight
box on
legend('DBO优化K-means')
set(gca, 'FontSize', 10)% 优化结果输出
distance_str={'sqeuclidean','cityblock','cosine'};
disp('蜣螂优化算法DBO优化K-means聚类: ');
disp(['最佳聚类数: ',num2str(round(pos(1)))])
disp(['最佳距离度量: ',distance_str{1,round(pos(2))}])

运行结果如下：

蜣螂优化算法DBO优化K-means结果：

蜣螂优化算法DBO优化K-means收敛曲线：

优化结果输出：

五、使用的数据

六、完整代码获取

PCA+DBO+K-means聚类