
目录
4.博弈模型
4.1.Nash平衡点和帕雷托最优
4.2.囚徒困境
4.3.智猪博弈
4.4.脏脸之谜
5.军事问题数学建模
5.1.兰彻斯特作战模型
5.1.1.一般战斗模型
5.1.2游击战模型
5.1.3.混合战模型
5.2.硫磺岛战役
4.博弈模型
本讲介绍博弈模型,包括博弈论(Game theory,又称对策论)中最基本的一些概念,以及非合作博弈论中的纳什平衡和帕雷托最优概念,同时介绍博弈论中的几个著名案例:囚徒困境、智猪博弈、脏脸之谜等。

博弈有5个基本要素:
-
局中人(选手)参与博弈的个人或团体。
-
策略(对策)可供局中人选择的行动方案。
-
赢利(获益)局中人的收益或支付。
-
信息 在策略选择中,信息是最关键的因素。
-
均衡 博弈的最终结果。
n人博弈模型的几个符号约定:
选手集:N={1, 2, …, n}
策略集:S1, S2, ..., Sn
决策集:D∈S=S1xS2x···x Sn
赢利函数:f1,f2, ..., fn D→R
例如:田忌赛马
S齐=S田={(上中下), {中下上}, {下上中}, {上下中}, {中上下}, {下中上}}
f齐{(上中下), (下上中)} = 0
f田{(上中下), (下上中)} = 1
下面讨论合作与不合作两种情形下的博弈。
如果选手k知道了其他选手的策略xi,(i=1,2,…,n,i≠k),自然希望取策略 xk∈Sk
4.1.Nash平衡点和帕雷托最优
定义选手k的合理反应集为
Rk={(x1,.., xn)∈D|(x1, ..., xn)使得(*)成立}
各选手都希望好、决策在各自的合理反应集中,所以称(x1, ..., xn)∈R1∩···∩Rn
为n人非合作对策的一个纳什平衡点。
对于Nash平衡点,在别人不改变对策的情况下,每个选手的对策都是最好的,故他们都不会轻易去改变自己的对策。所以,非合作博弈的解将在Nash平衡点处出现。
Nash定理 非零和非合作博弈的Nash平衡点一定存在
问题 Nash平衡点对博弈各方是否一定是最优的?
再考虑合作情形。
记f=(f1,f2, ..., fn)
定义:Dn={x∈D|f(x)≥f(x0)} x0是纳什平衡点
Dn称为合理集,最终的合作决策必定出自合理集中。
决策x∈D称为帕雷托(Pareto)最优的是指:D中不存在决策y使得f(y)>f(x)
4.2.囚徒困境
囚徒困境——非零和博弈
设两偷盗犯因被发现藏有被盗物品而被拘留。现被分别单独关押。两人都知道,如果都不承认偷盗,将以窝赃罪各判1年监禁;如果都承认,将以偷盗罪各判5年。但如果一人招认而另一人不承认,则坦白者将从宽处理获得释放,而抗拒者从严被判10年。这两个囚犯该如何选择自己的最优策略?
两个囚犯的策略集都是{x(招认), y(不招认)}
盈利函数分别为:
f1(x,x) = -5
f1(x,y) = 0
f1(y,x) = -10
f1(y,y) = -1
f2(x,x) = -5
f2(x,y) = -10
f2(y,x) = 0
f2(y,y) = -1
各自的合理反应集为:
R1 = {(x,x), (x, y)}
R2 = {(x,x),(y,x)}
4.3.智猪博弈
智猪博弈一弱势方的抉择
猪圈里有一头大猪,一头小猪。猪圈的一头有一个食槽,另一头有一个控制猪食供应的按钮按一次按钮,有10个单位的猪食入槽,但是按按钮要付出两个单位的跑动成本。若大猪先到食槽则大猪吃到9个单位猪食,小猪吃到1个单位;若两猪同时到达食槽,大猪吃7个单位猪食,小猪吃3个单位;若小猪先到,大猪吃6个单位,小猪吃4个单位。
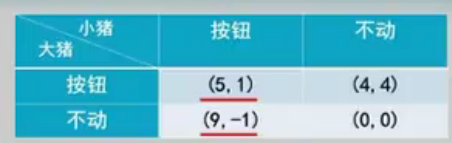
大猪按钮,小猪不动
4.4.脏脸之谜
脏脸之谜一共同知识
三姐妹从外面回到家里,她们的脸都是脏的,但她们自己并不知道。母亲见到她们后说道:“你们三人中至少有一个人的脸是脏的”,她们没有反应,因为这是一个显然的事实,她们认为母亲说的是一句“废话”。但当母亲追问一句“你们知道是谁吗?”她们先是互相看了一下,然后都脸红了,都知道自己的脸是脏的,这是为什么?
共同知识一每个人都知道这个事实,每个人都知道每个人都知道这个事实,每个人都知道每个人都知道每个人都知道这个事实,…
5.军事问题数学建模
5.1.兰彻斯特作战模型
第一次世界大战时提出的预测战争结局的模型
只考虑双方兵力多少和战斗力强弱。
兵力:
-
因战斗减员而减少
-
因非战斗减员而减少
-
因增援而增加
战斗力:
-
与射击率(单位时间的射击次数)、射击命中率以及战争的类型(常规战、游击战)等有关。
5.1.1.一般战斗模型
假设:
-
每一方的战斗减员率取决于双方的兵力和战斗力,用f(x,y)和g(x,y)表示。
-
每一方的增员率是给定的函数,用u(t)和v(t)表示。
模型如下:
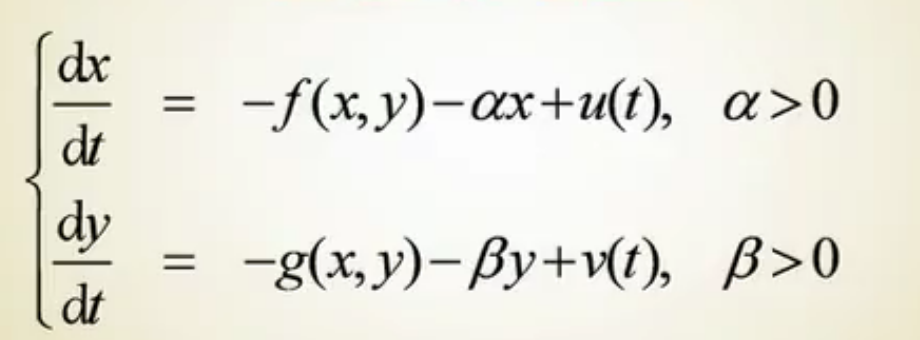
-f(x,y) 单位时间内因为战斗减员而减少的兵力数
-ax 单位时间内因非战斗减员而减少的兵力数量
u(t) 单位时间内因增援而增加的兵力数量
dx/dt 单位时间内增加或减少的兵力数量
-g(x,y) 则是乙方的

将非战斗减员与增员归于初值中,则模型进一步简化为:
常规战模型相轨线

这就是平方律模型
5.1.2游击战模型
甲乙双方都用游击部队作战。
甲方士兵在乙方士兵看不到的某个面积为S的隐蔽区域内活动,乙方士兵不是向甲方士兵开火,而是向这个隐蔽区域射击,并且不知道杀伤情况。这时甲方战斗减员率不仅与乙方兵力有关,而且随着甲方兵力的增加而增加。
f可简单假设为:
f = ay = (cx)y = cxy
乙方的战斗有效系数
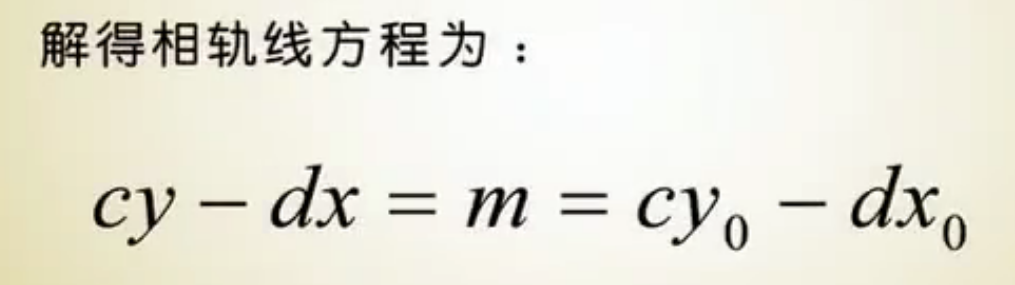
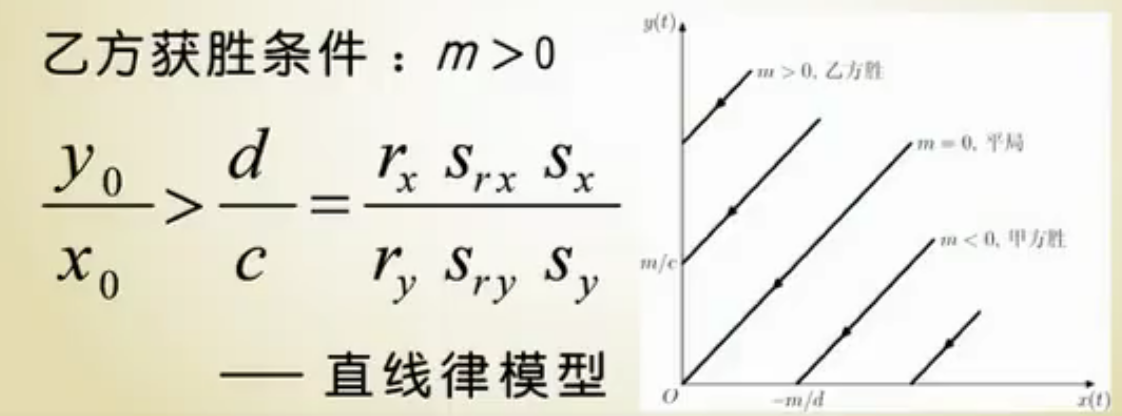
5.1.3.混合战模型
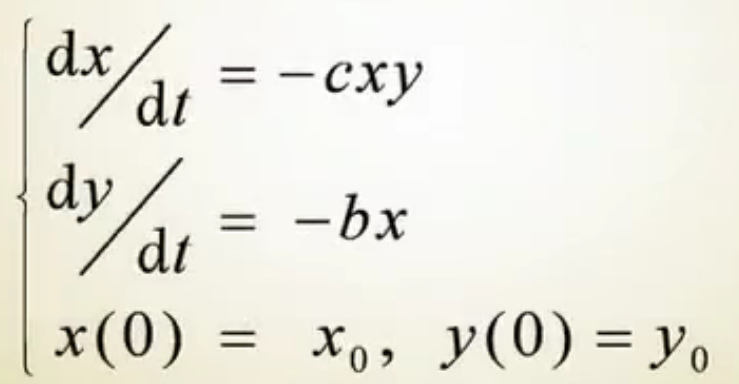

5.2.硫磺岛战役
思考题



(黑马))
的回归预测 多输入单输出【Matlab代码#68】)
文件中)


![练习8 Web [GYCTF2020]Blacklist](http://pic.xiahunao.cn/练习8 Web [GYCTF2020]Blacklist)




)






