文章目录
- 发现宝藏
- 【考生须知】
- 试题 A \mathrm{A} A : 特殊日期
- 试题 B: 与或异或
- 试题 C : \mathrm{C}: C: 平均
- 试题 D: 棋盘
- 试题 E : \mathrm{E}: E: 互质数的个数
- 试题 F: 阶乘的和
- 试题 G: 小蓝的旅行计划
- 试题 H: 太阳
- 试题 I: 高塔
- 试题 J \mathrm{J} J : 反异或 01 串
发现宝藏
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。【宝藏入口】。
【考生须知】
考试开始后,选手亘先下载题目,并使用考场现场公布的解压密码解压试题。
考试时间为 4 小时。考试期间选手可渕览自己已经提交的答案, 被浏览的答案允许拷贝。时间截止后,将无法继续提交或测览答案。
对同一题目,选手可多次提交答案,以最后一次提交的答案为准。
选手必须通过浏笕器方式提交自己的答案。选手在其它位置的作答或其它方式提交的答案无效。
试题包含 “结果填空” 和 “程序设计” 两种題型。
结果填空题: 要求选手根据题目描述直接填写结果。求解方式不搌。不要求源代码。把结果填空的答案直接通过网页提交即可, 不要书写多余的内容。
程序设计题: 要求选手设计的程序对于给定的输入能给出正确的输出结果。考生的程序只有能运行出正确结果才有机会得分。
注意: 在评卷时使用的输入数据与试卷中给出的示例数据可能是不同的。选手的程序必须是通用的, 不能只对试卷中给定的数据有效。
所有源码必须在同一文件中。调试通过后,拷贝提交。
注意: 不要使用 package 语句。
注意: 选手代码的主类名必须为: Main, 否则会被判为无效代码。
注意: 如果程序中引用了类库, 在提交时必须将 import 语句与程序的其他部分同时提交。只允许使用 Java 自带的类库。
试题 A \mathrm{A} A : 特殊日期
本虞总分: 5 分
【问题描述】
记一个日期为 y y y y yy 年 m m m m mm 月 d d d d dd 日,统计从 2000 年 1 月 1 日 (含) 到 2000000 年 1 月 1 日 (含), 有多少个日期满足年份 y y y y yy 是月份 m m m m mm 的倍数, 同时也是 d d d d dd 的倍数。
当年份是 4 的倍数而不是 100 的倍数或者年份是 400 的倍数时, 这一年是闰年,其他的年份都不是闰年。
【答案提交】
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
试题 B: 与或异或
本题总分: 5 分
【问题描述】
小蓝有一张门电路的逻辑图, 如下图所示:
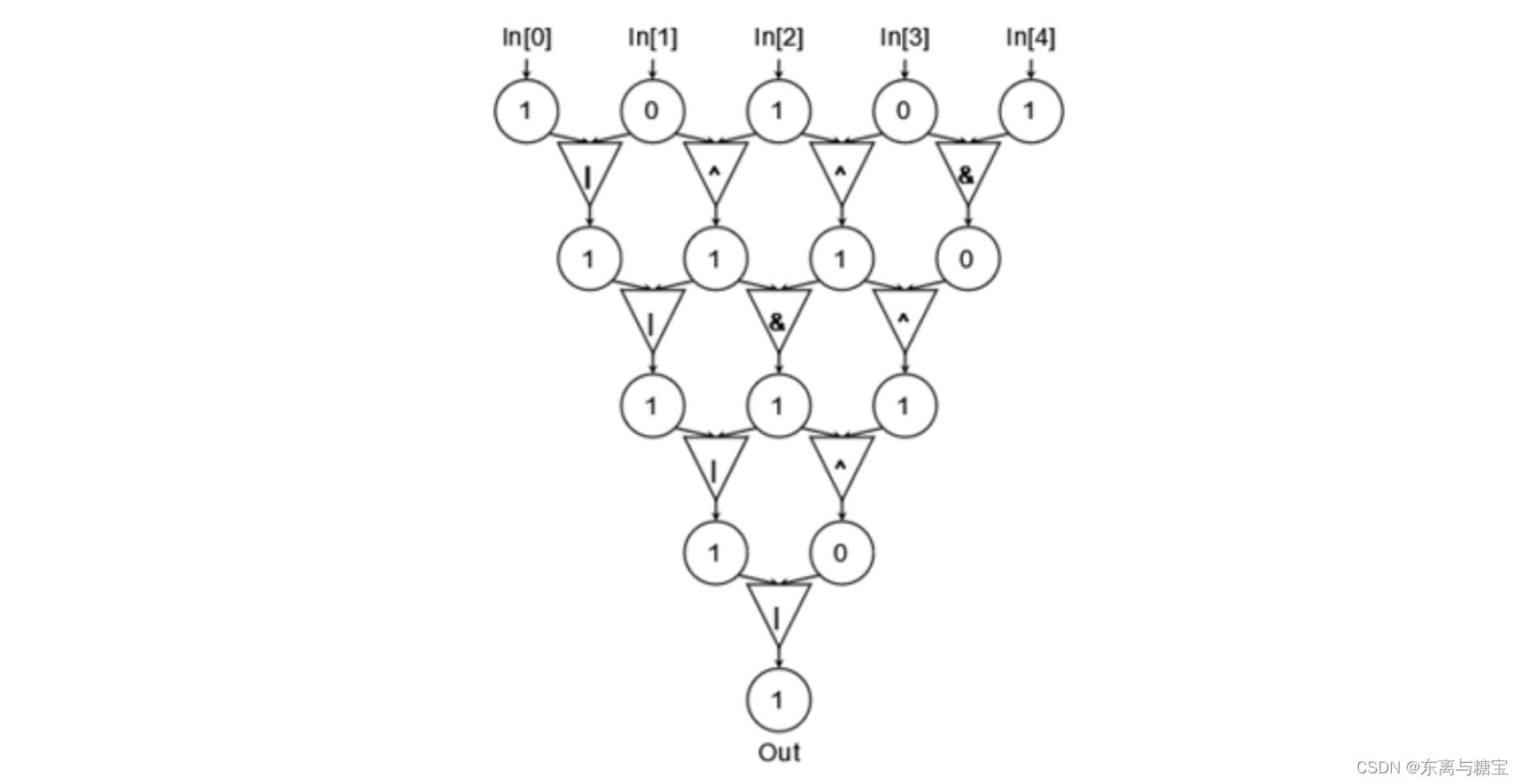
图中每个三角形代表着一种门电路, 可能是与门、或门、异或门中的任何一种, 它接受上一层中的两个圆形中的数据作为输入, 产生一个输出值输出到下一级 (如图中箭头所示)。图中圆形表示的是暂存的输出结果, 取值只可能是 0 或 1 , 为了便于表示我们用 arr [ i ] [ j ] \operatorname{arr}[i][j] arr[i][j] 表示第 i ( 0 ≤ i ≤ 4 ) i(0 \leq i \leq 4) i(0≤i≤4) 行第 j ( 0 ≤ j ≤ i ) j(0 \leq j \leq i) j(0≤j≤i) 个圆形的值。其中 arr [ 0 ] = ( In [ 0 ] , In [ 1 ] , In [ 2 ] , In [ 3 ] , In [ 4 ] ) \operatorname{arr}[0]=(\operatorname{In}[0], \operatorname{In}[1], \operatorname{In}[2], \operatorname{In}[3], \operatorname{In}[4]) arr[0]=(In[0],In[1],In[2],In[3],In[4]) 表示的是输入数据, 对于某个 arr [ i ] [ j ] ( i ≤ 0 ) \operatorname{arr}[i][j](i \leq 0) arr[i][j](i≤0), 计算方式为 arr [ i ] [ j ] = arr [ i − 1 ] [ j ] op arr [ i − 1 ] [ j + 1 ] \operatorname{arr}[i][j]=\operatorname{arr}[i-1][j] \operatorname{op} \operatorname{arr}[i-1][j+1] arr[i][j]=arr[i−1][j]oparr[i−1][j+1], 其中 o p o p op 表示的是将 arr [ i − 1 ] [ j ] 、 arr [ i − 1 ] [ j + 1 ] \operatorname{arr}[i-1][j] 、 \operatorname{arr}[i-1][j+1] arr[i−1][j]、arr[i−1][j+1] 作为输入, 将 arr [ i ] [ j ] \operatorname{arr}[i][j] arr[i][j] 作为输出的那
个门电路, 与门、或门、异或门分别对应于按位与 (&)、按位或 (1)、按位异或 (^) 运算符。
现在已知输入为 In [ 0 ] = 1 , In [ 1 ] = 0 , In [ 2 ] = 1 , In [ 3 ] = 0 , In [ 4 ] = 1 \operatorname{In}[0]=1, \operatorname{In}[1]=0, \operatorname{In}[2]=1, \operatorname{In}[3]=0, \operatorname{In}[4]=1 In[0]=1,In[1]=0,In[2]=1,In[3]=0,In[4]=1, 小蓝想要使得最终的输出 Out 的值为 1, 请问一共有多少种不同的门电路组合方式?其中上图中显示的就是一种合法的方式。
【答案提交】
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
试题 C : \mathrm{C}: C: 平均
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 10 分
【问题描述】
有一个长度为 n n n 的数组 ( n n n 是 10 的倍数), 每个数 a i a_{i} ai 都是区间 [ 0 , 9 ] [0,9] [0,9] 中的整数。小明发现数组里每种数出现的次数不太平均, 而更改第 i i i 个数的代价为 b i b_{i} bi, 他想更改若干个数的值使得这 10 种数出现的次数相等 (都等于 n 10 \frac{n}{10} 10n ), 请问代价和最少为多少。
【输入格式】
输入的第一行包含一个正整数 n n n 。
接下来 n n n 行, 第 i i i 行包含两个整数 a i , b i a_{i}, b_{i} ai,bi, 用一个空格分隔。
【输出格式】
输出一行包含一个正整数表示答案。
【样例输入】
10 \begin{array}{lll}10\end{array} 10
1 1 \begin{array}{lll}1 & 1\end{array} 11
1 2 \begin{array}{lll}1 & 2\end{array} 12
1 3 \begin{array}{lll}1 & 3\end{array} 13
2 4 \begin{array}{lll}2 & 4 \end{array} 24
2 5 \begin{array}{lll}2 & 5\end{array} 25
2 6 \begin{array}{lll}2& 6\end{array} 26
3 7 \begin{array}{lll}3& 7\end{array} 37
3 8 \begin{array}{ll}3 & 8\end{array} 38
3 9 \begin{array}{ll}3 & 9 \end{array} 39
4 10 \begin{array}{ll}4 & 10\end{array} 410
【样例输出】
27 \begin{array}{lll}27\end{array} 27
【样例说明】
只更改第 1 , 2 , 4 , 5 , 7 , 8 1,2,4,5,7,8 1,2,4,5,7,8 个数, 需要花费代价 1 + 2 + 4 + 5 + 7 + 8 = 27 1+2+4+5+7+8=27 1+2+4+5+7+8=27 。
【评测用例规模与约定】
对于 20 % 20 \% 20% 的评测用例, n ≤ 1000 n \leq 1000 n≤1000;
对于所有评测用例, n ≤ 100000 , 0 < b i ≤ 2 × 1 0 5 n \leq 100000,0<b_{i} \leq 2 \times 10^{5} n≤100000,0<bi≤2×105 。
试题 D: 棋盘
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0MB 本题总分: 10 分
【问题描述】
小蓝拥有 n × n n \times n n×n 大小的棋盘, 一开始棋盘上全都是白子。小蓝进行了 m m m 次操作, 每次操作会将棋盘上某个范围内的所有棋子的颜色取反 (也就是白色棋子变为黑色, 黑色棋子变为白色)。请输出所有操作做完后棋盘上每个棋子的颜色。
【输入格式】
输入的第一行包含两个整数 n , m n, m n,m, 用一个空格分隔, 表示棋盘大小与操作数。
接下来 m m m 行每行包含四个整数 x 1 , y 1 , x 2 , y 2 x_{1}, y_{1}, x_{2}, y_{2} x1,y1,x2,y2, 相邻整数之间使用一个空格分隔, 表示将在 x 1 x_{1} x1 至 x 2 x_{2} x2 行和 y 1 y_{1} y1 至 y 2 y_{2} y2 列中的棋子颜色取反。
【输出格式】
输出 n n n 行, 每行 n n n 个 0 或 1 表示该位置棋子的颜色。如果是白色则输出 0 , 否则输出 1 。
【样例输入】
3 3 \begin{array}{lll}3 & 3\end{array} 33
1 1 2 2 \begin{array}{llll}1 & 1 & 2 & 2\end{array} 1122
2 2 3 3 \begin{array}{llll}2 & 2 & 3 & 3\end{array} 2233
1 1 3 3 \begin{array}{llll}1 & 1 & 3 & 3\end{array} 1133
【样例输出】
001 \begin{array}{lll}001\end{array} 001
010 \begin{array}{lll}010\end{array} 010
100 \begin{array}{lll}100\end{array} 100
【评测用例规模与约定】
对于 30 % 30 \% 30% 的评测用例, n m ≤ 500 n \mathrm{~m} \leq 500 n m≤500 ;
对于所有评测用例, 1 ≤ n , m ≤ 2000 , 1 ≤ x 1 ≤ x 2 ≤ n , 1 ≤ y 1 ≤ y 2 ≤ m 1 \leq n, m \leq 2000,1 \leq x_{1} \leq x_{2} \leq n, 1 \leq y_{1} \leq y_{2} \leq m 1≤n,m≤2000,1≤x1≤x2≤n,1≤y1≤y2≤m 。
试题 E : \mathrm{E}: E: 互质数的个数
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 15 分
【问题描述】
给定 a , b a, b a,b, 求 1 ≤ x < a b 1 \leq x<a^{b} 1≤x<ab 中有多少个 x x x 与 a b a^{b} ab 互质。由于答案可能很大, 你只需要输出答案对 998244353 取模的结果。
【输入格式】
输入一行包含两个整数分别表示 a , b a, b a,b, 用一个空格分隔。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入 1】
2 5 \begin{array}{lll}2 & 5\end{array} 25
【样例输出 1】
16 \begin{array}{lll}16\end{array} 16
【样例输入 2】
12 7 \begin{array}{lll}12 & 7\end{array} 127
【样例输出 2】
11943936 \begin{array}{lll}11943936\end{array} 11943936
【评测用例规模与约定】
对于 30 % 30 \% 30% 的评测用例, a b ≤ 1 0 6 a^{b} \leq 10^{6} ab≤106;
对于 70 % 70 \% 70% 的评测用例, a ≤ 1 0 6 , b ≤ 1 0 9 a \leq 10^{6}, b \leq 10^{9} a≤106,b≤109 ;
对于所有评测用例, 1 < a ≤ 1 0 9 , 1 ≤ b ≤ 1 0 18 1<a \leq 10^{9}, 1 \leq b \leq 10^{18} 1<a≤109,1≤b≤1018 。
试题 F: 阶乘的和
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 15 分
【问题描述】
给定 n n n 个数 A i A_{i} Ai, 问能满足 m ! m ! m! 为 ∑ i = 1 n ( A i ! ) \sum_{i=1}^{n}\left(A_{i} !\right) ∑i=1n(Ai!) 的因数的最大的 m m m 是多少。其中 m m m ! 表示 m m m 的阶乘, 即 1 × 2 × 3 × ⋯ × m 1 \times 2 \times 3 \times \cdots \times m 1×2×3×⋯×m 。
【输入格式】
输入的第一行包含一个整数 n n n 。
第二行包含 n n n 个整数, 分别表示 A i A_{i} Ai, 相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
3 \begin{array}{lll}3\end{array} 3
2 2 2 \begin{array}{lll}2&2&2\end{array} 222
【样例输出】
【评测用例规模与约定】
对于 40 % 40 \% 40% 的评测用例, n ≤ 5000 n \leq 5000 n≤5000 ;
对于所有评测用例, 1 ≤ n ≤ 1 0 5 1 ≤ A i ≤ 1 0 9 1 \leq n \leq 10^{5} 1 \leq A_{i} \leq 10^{9} 1≤n≤1051≤Ai≤109 。
试题 G: 小蓝的旅行计划
时间限制: 5.0 s 5.0 \mathrm{~s} 5.0 s 内存限制: 512.0MB 本题总分: 20 分
【问题描述】
小蓝正计划进行一次漫长的旅行。小蓝计划开车完成这次旅行。显然他在途中需要加油, 否则可能无法完成这次旅行。
小蓝要依次经过 n n n 个地点, 其中从第 i − 1 i-1 i−1 个地点到达第 i i i 个地点需要消耗 D i s i D i s_{i} Disi 升油。小蓝经过的每个地点都有一个加油站, 但每个加油站的规定也不同。在第 i i i 个加油站加 1 升油需要 Cost i _{i} i 的费用, 且在这个加油站最多只能加 Lim i _{i} i升油。
小蓝的车的油箱也有容量限制, 他的车上最多只能装载 m m m 升油。
一开始小蓝的油箱是满的, 请问小蓝需要准备多少钱才能顺利完成他的旅行计划。如果小蓝按给定条件无论准备多少钱都不能完成他的旅行计划, 请输出 -1 。
【输入格式】
输入的第一行包含两个整数 n m n \mathrm{~m} n m, 用一个空格分隔。
接下来 n n n 行每行包含 3 个整数 Dis i C o s t i Lim i _{i} Cost _{i} \operatorname{Lim}_{i} iCostiLimi, 相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
4 5 \begin{array}{lll}4 & 5\end{array} 45
2 9 2 \begin{array}{lll}2 & 9 & 2\end{array} 292
4 5 6 \begin{array}{lll}4 & 5 & 6\end{array} 456
3 2 2 \begin{array}{lll}3 & 2 & 2\end{array} 322
4 1 3 \begin{array}{lll}4 & 1 & 3\end{array} 413
【样例输出】
38 \begin{array}{lll}38\end{array} 38
【评测用例规模与约定】
对于 30 % 30 \% 30% 的评测用例, n n n Dis i Cost i Lim i m ≤ 300 _{i} \operatorname{Cost}_{i} \operatorname{Lim}_{i} m \leq 300 iCostiLimim≤300 ;
对于 60 % 60 \% 60% 的评测用例, n n n Dis i _{i} i Cost i Lim i m ≤ 5000 _{i} \operatorname{Lim}_{i} m \leq 5000 iLimim≤5000 ;
对于所有评测用例, 1 ≤ n ≤ 2 × 1 0 5 , 1 ≤ 1 \leq n \leq 2 \times 10^{5}, 1 \leq 1≤n≤2×105,1≤ Dis i _{i} i Lim i m ≤ 1 0 9 , 1 ≤ _{i} m \leq 10^{9}, 1 \leq im≤109,1≤ Cost i ≤ _{i} \leq i≤ 40000 。
试题 H: 太阳
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 20 分
【问题描述】
这天, 小蓝在二维坐标系的点 ( X , Y ) (X, Y) (X,Y) 上放了一个太阳, 看做点光源。
他拿来了 n n n 条线段, 将它们平行于 x x x 轴放置在了坐标系中, 第 i i i 条线段的左端点在 x i , y i x_{i}, y_{i} xi,yi, 长度为 l i l_{i} li 。线段之间不会有重合或部分重合的情况 (但可能出现端点相交)。小蓝想知道有多少条线段能被太阳照亮 (一条线段有长度大于 0 的部分被照亮就算)。
【输入格式】
输入的第一行包含三个正整数 n , X , Y n, X, Y n,X,Y, 相邻整数之间使用一个空格分隔。
接下来 n n n 行, 第 i i i 行包含三个整数 x i , y i , l i x_{i}, y_{i}, l_{i} xi,yi,li, 相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个正整数表示答案。
【样例输入】
3 1 2000000 \begin{array}{lll}3 & 1 & 2000000\end{array} 312000000
5 3 5 \begin{array}{lll}5& 3& 5\end{array} 535
6 2 4 \begin{array}{lll}6& 2& 4\end{array} 624
0 1 0 \begin{array}{lll}0&1 & 0\end{array} 010
【样例输出】
2 \begin{array}{lll}2\end{array} 2
【样例说明】
第一条线段在最上面被照亮, 第二条线段被第一条完全挡住, 第三条线段左边的一段能被照亮。
【评测用例规模与约定】
对于 30 % 30 \% 30% 的评测用例, n ≤ 1000 n \leq 1000 n≤1000;
对于所有评测用例, 1 ≤ n ≤ 100000 , 0 ≤ x i , X ≤ 1 0 7 , 0 < y i ≤ 1 0 5 , 0 < l i ≤ 1 \leq n \leq 100000,0 \leq x_{i}, X \leq 10^{7}, 0<y_{i} \leq 10^{5}, 0<l_{i} \leq 1≤n≤100000,0≤xi,X≤107,0<yi≤105,0<li≤ 100 , 1 0 6 < Y ≤ 1 0 7 100,10^{6}<Y \leq 10^{7} 100,106<Y≤107 。
试题 I: 高塔
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 25 分
【问题描述】
小蓝正在玩一个攀登高塔的游戏。高塔的层数是无限的, 但游戏最多只有 n n n 回合。
小蓝一开始拥有 m m m 点能量, 在每个回合都有一个值 A i A_{i} Ai 表示小蓝的角色状态。小蓝每回合可以选择消费任意点能量 C i C_{i} Ci (最低消费 1 点, 没有上限), 他在这回合将最多可以向上攀爬 A i ⋅ C i A_{i} \cdot C_{i} Ai⋅Ci 层。实际攀爬的层数取决于小蓝自己在这回合的表现, 不过最差也会向上爬一层。
当某回合小蓝的能量点数耗尽, 那么在完成这个回合后, 游戏结束。 n n n 回合结束后,不管能量还有没有剩余,游戏都会直接结束。
给出小蓝每回合的 A i A_{i} Ai 和自己一开始的能量点数 m m m 。小蓝想知道有多少种不同的可能出现的游玩过程。如果小蓝在两种游玩过程中的任一对应回合花费的能量点数不同或该回合结束时所处层数不同, 那么这两种游玩过程就被视为不同。
【输入格式】
输入的第一行包含两个整数 n , m n, m n,m, 用一个空格分隔。
第二行包含 n n n 个整数 A i A_{i} Ai, 相邻整数之间使用一个空格分隔, 表示小蓝每回合的状态值。
【输出格式】
输出一行包含一个整数表示给定条件下不同游玩过程的数量。由于答案可能很大,你只需要输出答案对 998244353 取模的结果
【样例输入】
9 15 \begin{array}{lll} 9 & 15\end{array} 915
3 2 5 7 1 4 6 8 3 \begin{array}{llllllllll}3 & 2 & 5 & 7 & 1 & 4 & 6 & 8 & 3\end{array} 325714683
【样例输出】
392149233 \begin{array}{lll}392149233\end{array} 392149233
【评测用例规模与约定】
对于 40 % 40 \% 40% 的评测用例, n ≤ 300 , m ≤ 500 n \leq 300, m \leq 500 n≤300,m≤500 ;
对于所有评测用例, 1 ≤ n ≤ 2 × 1 0 5 , n ≤ m ≤ 1 0 18 , 1 ≤ A i ≤ 1 0 9 1 \leq n \leq 2 \times 10^{5}, n \leq m \leq 10^{18}, 1 \leq A_{i} \leq 10^{9} 1≤n≤2×105,n≤m≤1018,1≤Ai≤109 。
试题 J \mathrm{J} J : 反异或 01 串
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0MB 本题总分: 25 分
【问题描述】
初始有一个空的 01 串, 每步操作可以将 0 或 1 添加在左侧或右侧。也可以对整个串进行反异或操作: 取 s ′ = s ⊕ rev ( s ) s^{\prime}=s \oplus \operatorname{rev}(s) s′=s⊕rev(s), 其中 s s s 是目前的 01 串, ⊕ \oplus ⊕ 表示逐位异或, rev ( s ) \operatorname{rev}(s) rev(s) 代表将 s s s 翻转, 也就是说取中心位置并交换所有对称的两个位置的字符。例如, rev ( 0101 ) = 1010 rev ( 010 ) = 010 rev ( 0011 ) = 1100 \operatorname{rev}(0101)=1010 \operatorname{rev}(010)=010 \operatorname{rev}(0011)=1100 rev(0101)=1010rev(010)=010rev(0011)=1100 。
反异或操作最多使用一次 (可以不用, 也可以用一次)。
给定一个 01 串 T T T, 问最少需要添加多少个 1 才能从一个空 01 串得到 T T T 。在本题中 0 可以添加任意个。
【输入格式】
输入一行包含一个 01 串表示给定的 T T T 。
【输出格式】
输出一行包含一个整数, 表示需要最少添加多少个 1 。
【样例输入】
00111011 \begin{array}{lll}00111011\end{array} 00111011
【样例输出】
3 \begin{array}{lll}3\end{array} 3
【评测用例规模与约定】
对于 20 % 20 \% 20% 的评测用例, ∣ T ∣ ≤ 10 |T| \leq 10 ∣T∣≤10 ;
对于 40 % 40 \% 40% 的评测用例, ∣ T ∣ ≤ 500 |T| \leq 500 ∣T∣≤500 ;
对于 60 % 60 \% 60% 的评测用例, ∣ T ∣ ≤ 5000 |T| \leq 5000 ∣T∣≤5000 ;
对于 80 % 80 \% 80% 的评测用例, ∣ T ∣ ≤ 1 0 5 |T| \leq 10^{5} ∣T∣≤105;
对于所有评测用例, 1 ≤ ∣ T ∣ ≤ 1 0 6 1 \leq|T| \leq 10^{6} 1≤∣T∣≤106, 保证 T T T 中仅含 0 和 1 。
)
)

)




)



)



)

