目录
- 1. 朴素二分查找
- 2. 在排序数组中查找元素的第一个和最后一个位置
- 3. 搜索插入位置
- 4. x的平方根
- 5. 山脉数组的峰值索引
- 6. 寻找峰值
- 7. 寻找旋转排序数组中的最小值
- 8. 点名
1. 朴素二分查找
- 题目信息:
- 题目链接:
二分查找- 二分查找的使用前提为数据具有"二段性",在二分时,并不一定要进行2等分(1/3,1/4…)
- 二分查找的时间复杂度:O( l o g N log^N logN)
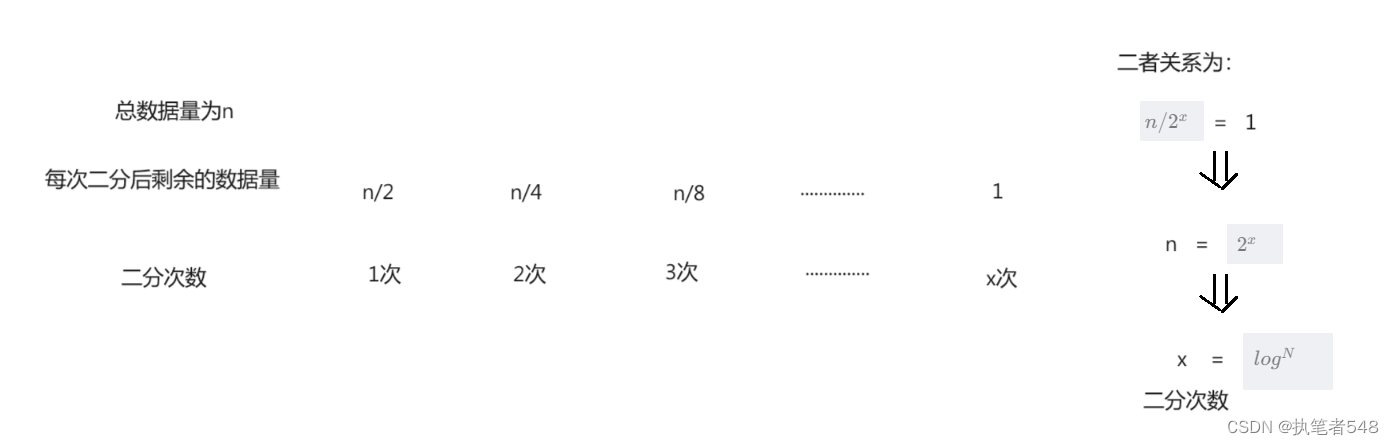
- 求mid的算法优化(原算法有溢出风险)
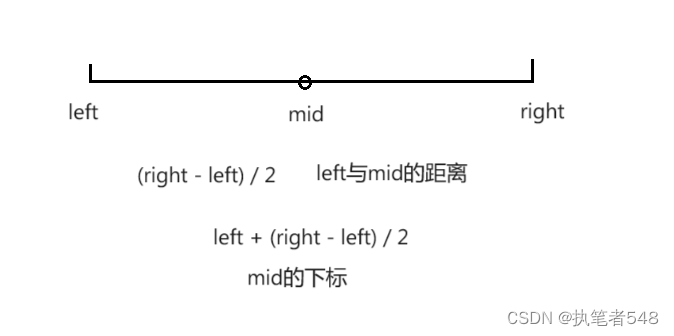
class Solution
{
public:int search(vector<int>& nums, int target) {int right = nums.size() - 1;int left = 0;while(right >= left){//此种算法存在溢出风险//int mid = (right + left) / 2;int mid = (right - left) / 2 + left;if(nums[mid] > target){right = mid - 1;}if(nums[mid] < target){left = mid + 1;}if(nums[mid] == target){return mid;}}return -1;}
};
2. 在排序数组中查找元素的第一个和最后一个位置
- 题目信息:
- 题目链接:
在排序数组查找元素的第一个与最后一个位置- 思路:向符合条件位置不断推进
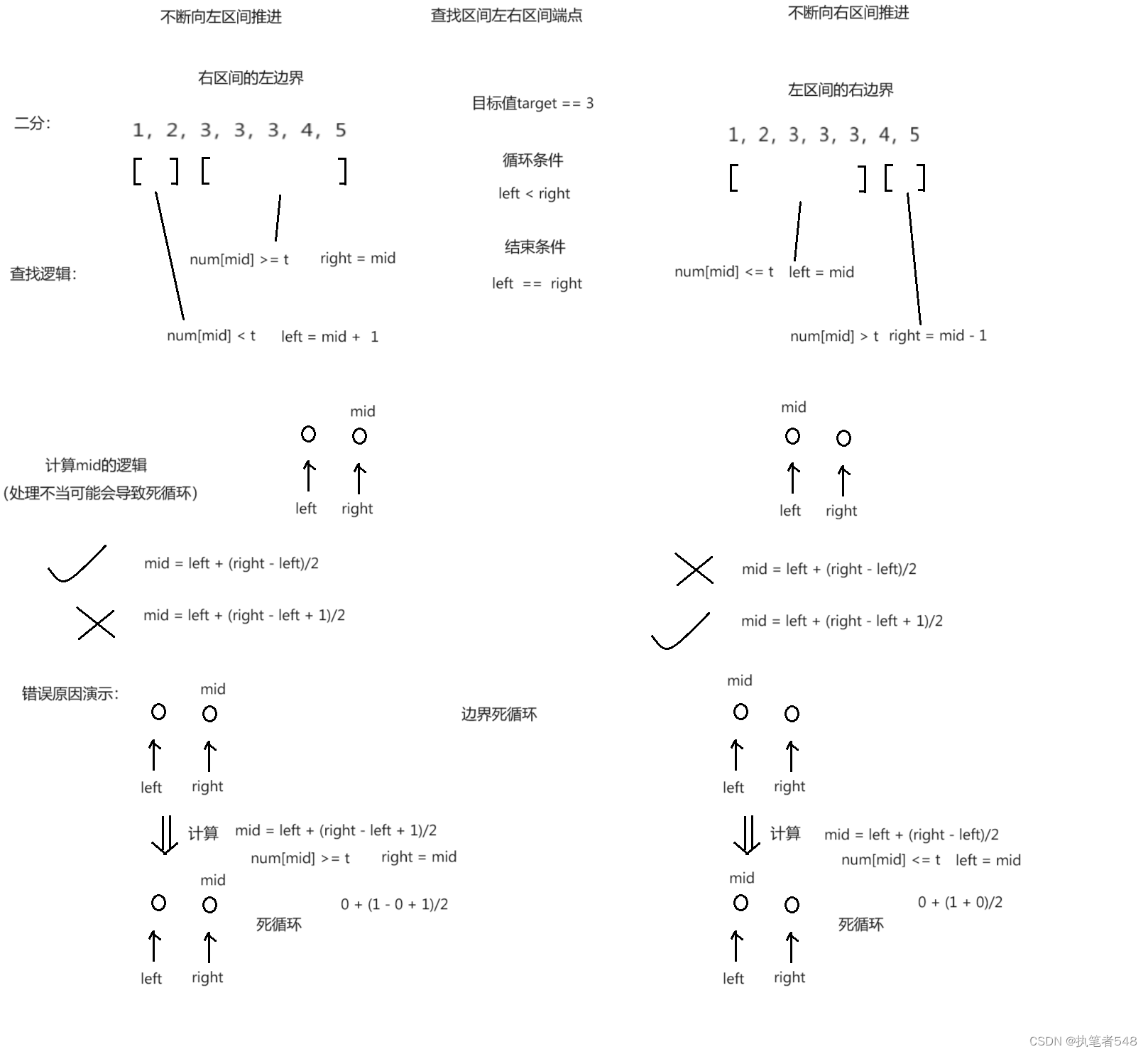
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int right = nums.size() - 1;int left = 0;vector<int> count(2,-1);//数据为空,特殊处理if(nums.size() == 0){return count;}//左端点while(left < right){//落到左区间int mid = left + (right - left) / 2;if(nums[mid] >= target){right = mid;}if(nums[mid] < target){left = mid + 1;}}if(nums[left] == target){count[0] = left;}right = nums.size() - 1;left = 0;//右端点while(left < right){//落到右区间int mid = left + (right - left + 1) / 2;if(nums[mid] > target){right = mid - 1;}if(nums[mid] <= target){left = mid;}}if(nums[left] == target){count[1] = left;}return count;}
};
3. 搜索插入位置
- 题目信息:
- 题目链接:
搜索插入位置- 思路:取大,右区间的左边界
class Solution
{
public:int searchInsert(vector<int>& nums, int target) {int left = 0;int right = nums.size();while(left < right){//小于,大于等于int mid = left + (right - left) / 2;if(nums[mid] < target){left = mid + 1;}if(nums[mid] >= target){right = mid;}}return left;}
};
4. x的平方根
- 题目信息:
- 题目链接:
x的平方根- 思路:暴力解法的优化,左区间的右边界,二段性
class Solution
{
public:int mySqrt(int x) {if(x < 1){return 0;}int left = 1;int right = x;while(left < right){//当left从0开始时,left + 1可能会溢出long long mid = left + (right - left + 1) / 2;//防止溢出if(mid * mid <= x){left = mid;}if(mid * mid > x){right = mid - 1;}}return left;}
};
5. 山脉数组的峰值索引
- 题目信息:
- 题目链接:
山脉数组的峰值索引- 思路:二分法,左区间右边界
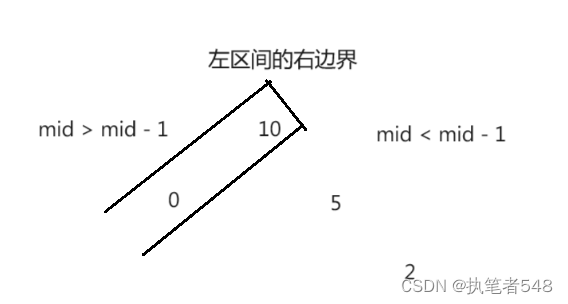
class Solution
{
public:int peakIndexInMountainArray(vector<int>& nums) {//左区间,右边界int left = 0;int right = nums.size() - 1;while(left < right){int mid = left + (right - left + 1) / 2;if(nums[mid] > nums[mid - 1]){left = mid;}if(nums[mid] < nums[mid - 1]){right = mid - 1;}}return left;}
};
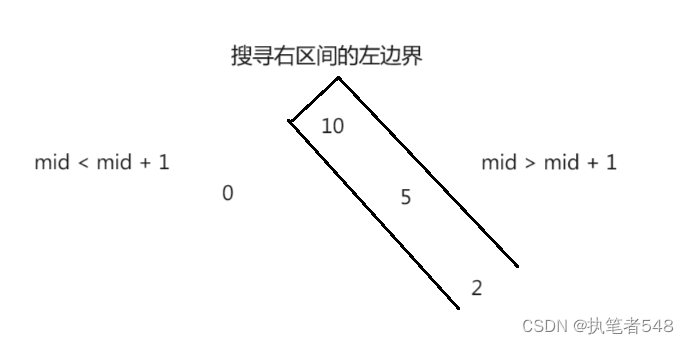
- 右区间的左边界
class Solution
{
public:int peakIndexInMountainArray(vector<int>& nums) {//右区间,左边界int left = 0;int right = nums.size() - 1;while(left < right){int mid = left + (right - left) / 2;if(nums[mid] < nums[mid + 1]){left = mid + 1;}if(nums[mid] > nums[mid + 1]){right = mid;}}return left;}
};
6. 寻找峰值
- 题目信息:
- 题目链接:
寻找峰值- 思路:二段性,右区间的左边界,不足三个数特殊化处理

class Solution
{
public:int findPeakElement(vector<int>& nums) {int left = 0;int right = nums.size() - 1;//特殊情况//数组值小于3if (nums.size() < 2){return 0;}if (nums.size() < 3){return nums[0] > nums[1] ? 0 : 1;}//右区间的左边界while (left < right){int mid = left + (right - left) / 2;if (nums[mid] < nums[mid + 1]){left = mid + 1;}if (nums[mid] > nums[mid + 1]){right = mid;}}return left;}
};
7. 寻找旋转排序数组中的最小值
- 题目信息:
- 题目链接:
寻找寻转排序数组中的最小值- 思路:右区间,左边界
class Solution
{
public:int findMin(vector<int>& nums) {//二段性,右区间,左边界int right = nums.size() - 1;int left = 0;while(left < right){int mid = left + (right - left) / 2;if(nums[mid] > nums[right]){left = mid + 1;}if(nums[mid] < nums[right]){right = mid;}}return nums[left];}
};
8. 点名
- 题目信息:
- 题目链接:
点名- 思路:(多解法,考察知识广度)
<1>二分法:右区间的左边界,学号等于下标,学号大于下标,边界问题!
<2> 哈希表法:时间复杂度O(n),空间复杂度O(n)
<3> 异或法
<4> 等差数列求和
<5> 暴力遍历法
class Solution {
public:int takeAttendance(vector<int>& records) {int left = 0;int right = records.size() - 1;while(left < right){int mid = left + (right - left) / 2;if(records[mid] == mid){left = mid + 1;}if(records[mid] > mid){right = mid;}}//边界问题,n-1个元素,n个学生,必定有一人缺席,缺席为学号最后一位的学生if(left == records.size() - 1 && left == records[left]){left++;}return left;}
};
- 等差数列
class Solution
{
public:int takeAttendance(vector<int>& records) {//等差数列求和,首项加末项乘以项数除以2int sum = ((0 + records.size()) * (records.size() + 1)) / 2;for(int i = 0; i < records.size(); i++){sum -= records[i];}return sum;}
};
- 哈希表
class Solution
{
public:int takeAttendance(vector<int>& records) {//哈希表法int n = records.size() + 1;int* hash = (int*)malloc(n * sizeof(int));//单位字节memset(hash, 0, n * sizeof(int));int i = 0;for(i = 0; i < records.size(); i++){hash[records[i]]++;}for(i = 0; i < n; i++){if(hash[i] == 0){break;}}return i;}
};
- 暴力遍历
class Solution
{
public:int takeAttendance(vector<int>& records) {//暴力遍历int cur = 0;while(cur < records.size()){if(cur != records[cur]){break;}cur++;}if(cur == records.size() - 1 && records[cur] == cur){cur++;}return cur;}
};
- 异或法
class Solution
{
public:int takeAttendance(vector<int>& records){//异或法int sum = 0;for(int i = 0; i < records.size() + 1; i++){sum ^= i;}for(int i = 0; i < records.size(); i++){sum ^= records[i];}return sum;}
};








)



)



)



)





