1. 请求参数的合法性校验

使用基于JSR303的校验框架实现，Springboot提供了JSR-303的支持，它就是spring-boot-starter-validation，他包括了很多的校验规则，只需要在模型中通过注解指定校验规则，在Controller方法上开启校验

2. JSR303的使用

比如说我们需要对我们的参数进行校验，为了代码的整洁性和美观性，又不想进行异常处理，这时就需要使用JSR303校验框架

2.1 接口参数前添加@Validated注解

    @ApiOperation("新增课程基础信息")@PostMapping("/course")public CourseBaseInfoDto createCourseBase(@RequestBody @Validated AddCourseDto addCourseDto) {//机构idLong companyId = 1232141425L;CourseBaseInfoDto courseBase = courseBaseInfoService.createCourseBase(companyId, addCourseDto);return courseBase;}

2.2 在参数模型中进行处理

比如

@Data
@ApiModel(value="AddCourseDto", description="新增课程基本信息")
public class AddCourseDto {@NotEmpty(message = "新增课程名称不能为空")@ApiModelProperty(value = "课程名称", required = true)private String name;}

2.3 进行全局异常处理

    //MethodArgumentNotValidException@ExceptionHandler(MethodArgumentNotValidException.class)@ResponseStatus(HttpStatus.INTERNAL_SERVER_ERROR)@ResponseBodypublic RestErrorResponse methodArgumentNotValidException(MethodArgumentNotValidException e){BindingResult bindingResult = e.getBindingResult();//存放错误信息List<String> errors = new ArrayList<>();bindingResult.getFieldErrors().stream().forEach(item ->{errors.add(item.getDefaultMessage());});//将list当中的错误信息拼接起来String errMessage = StringUtils.join(errors, ",");//记录异常log.error("系统异常{}",e.getMessage(),e);//解析出异常信息RestErrorResponse restErrorResponse = new RestErrorResponse(errMessage);return restErrorResponse;}

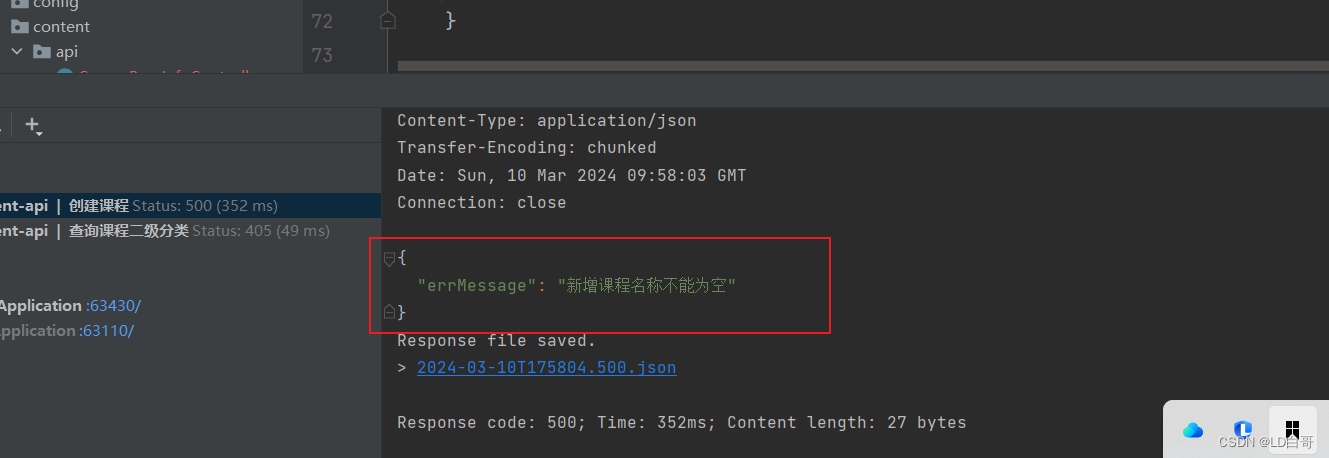
对于异常返回模型，请参照上个异常处理文章，有详情代码

3. 分组校验

如果对同一类型参数有两种校验，比如说添加课程，和更新课程，参数一样，但是校验的规则不一样，此时，就要用到分组校验

3.1 分组校验操作

3.1.1 设置分组类

/*** 用于分组检验*/
public class ValidationGroups {public interface Insert{};public interface Update{};public interface Delete{};
}

3.1.2 接口参数前表明校验组

下列代码表明参数的校验遵从的是添加组规则

    @ApiOperation("新增课程基础信息")@PostMapping("/course")public CourseBaseInfoDto createCourseBase(@RequestBody @Validated(ValidationGroups.Insert.class) AddCourseDto addCourseDto) {//机构idLong companyId = 1232141425L;CourseBaseInfoDto courseBase = courseBaseInfoService.createCourseBase(companyId, addCourseDto);return courseBase;}

3.1.2 接口模型中进行分组的校验规则

如下

@Data
@ApiModel(value="AddCourseDto", description="新增课程基本信息")
public class AddCourseDto {@NotEmpty(message = "新增课程名称不能为空",groups = {ValidationGroups.Insert.class})@NotEmpty(message = "修改课程名称不能为空",groups = {ValidationGroups.Update.class})@ApiModelProperty(value = "课程名称", required = true)private String name;}