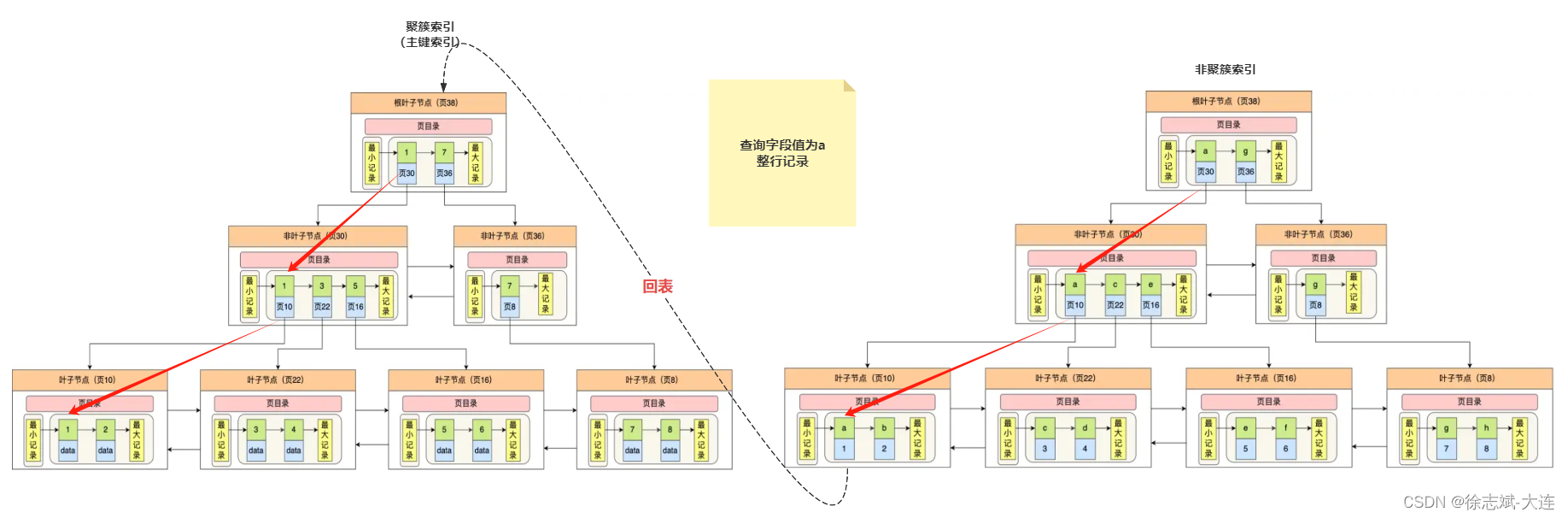
前言
智慧零售行业是在数字化浪潮中快速发展的一个领域,它利用先进的信息技术和大数据分析来提升零售业务的效率和顾客体验。智慧零售订单平台,具有跨平台、数据智能清洗和建模,以及更加丰富的数据展示形式等优势。智慧零售订单平台可以以文本、图表、图形和地图等高级方式清晰地统计和展示抽象的销售数据。今天小编就将为大家介绍一下如何使用葡萄城公司的嵌入式BI工具——Wyn商业智能搭建一个智慧零售订单平台。
Wyn 介绍
Wyn 商业智能专注于商业智能和数据分析需求,提供一站式数据分析能力,核心功能包括:多源数据整合、自助式 BI 分析、数据可视化、在线报表设计以及数据填报等,可以满足各种场景中的数据分析和平台的快速构建。并且有完善的学习和问题支持体系,从新手入门的新手训练营(线上视频课程)到后期高阶的功能文档、售后支持等等。构建了完整的产品生态系统。

平台构建
1)自主设计
在设计之前,先确定需要展示展示哪些数据,然后根据数据的特性选择合适的图表进行展示。比如展示销售额、订单数之类的统计数据最好是富文本或者指示器;想查看分布情况就使用地图类组件等等。根据想要展示的数据选择对应的图表。

2)模板创建
在设计时,前期的数据准备不尽相同,但是在最后的展示上常常是大同小异,这种情况下,我们就可以从葡萄城市场查找模板,然后直接通过模板创创建仪表板,然后替换使用的数据模型即可。
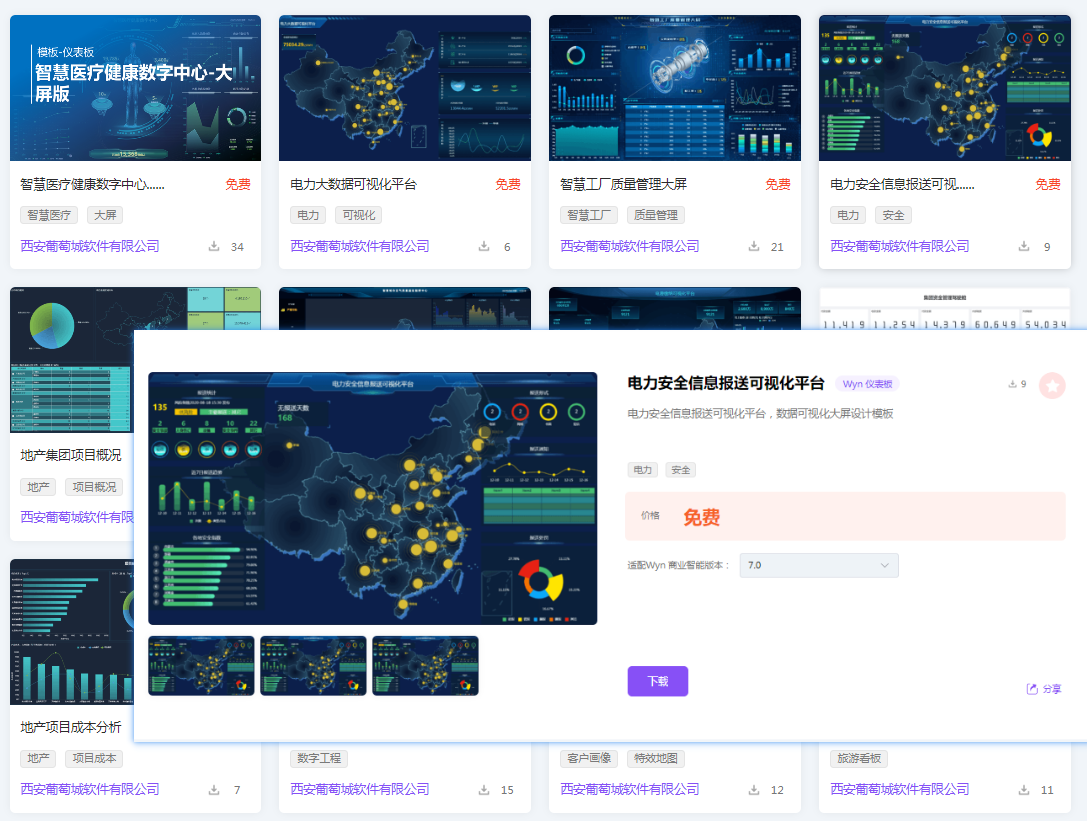
下载的模板在Wyn中导入,就可以通过模板快速创建:

3)数据替换
创建模板之后,找到对应的组件,更换绑定的数据就可以,这样就完成了一个仪表板的设计。
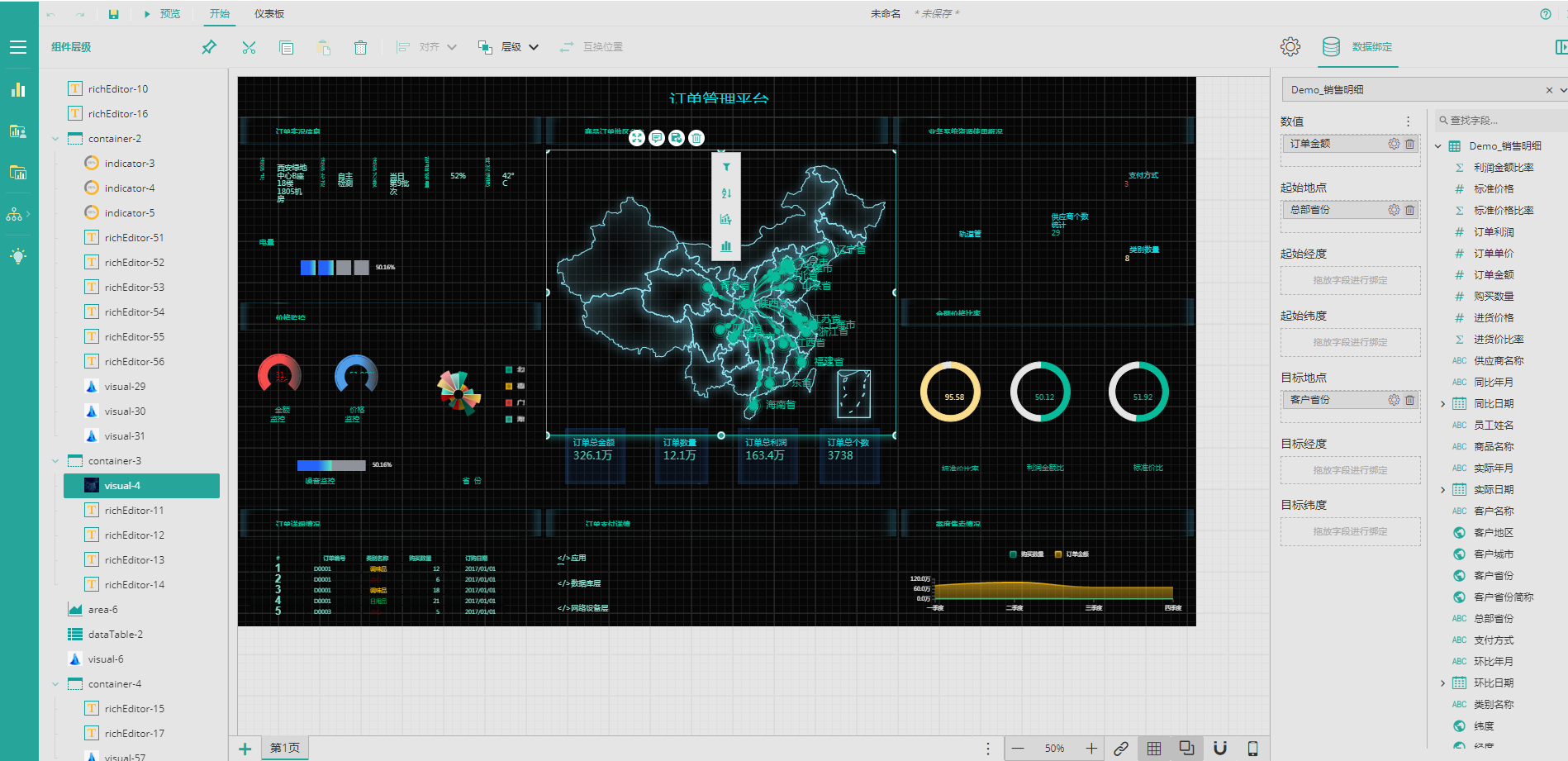
总结
随着技术的发展,所有行业都在向着数字化、智能化和信息化的方向发展。智慧零售已经成为不可逆转的趋势,Wyn 作为一个全面、完善且高效的智能化嵌入式BI产品,将帮助我们的零售企业在发展中抢占先机,更好地应对未来的挑战。我们鼓励所有零售商积极探索并应用Wyn平台,实现数字化转型,迎接智慧零售时代的到来!
扩展链接:
创意展示:打造数据大屏的炫酷天气预报插件
聊一聊数字孪生与3D可视化
探秘移动端BI:发展历程与应用前景解析