引言:数学问题解决中的语言模型挑战
数学问题解决是一个复杂的认知过程,它要求参与者不仅要掌握数学知识,还要能够进行多步骤的逻辑推理。近年来,大语言模型(LLMs)在解决问题方面展现出了显著的能力,但在数学问题解决方面的表现仍然不尽人意。这可能是因为数学问题解决本质上需要复杂的多步骤推理,而这正是当前LLMs所缺乏的。
尽管通过指令调整(Instruction Tuning)可以在一定程度上提升LLMs的数学解决能力,但现有的数学推理数据集规模有限,这限制了模型能力的进一步提升。例如,目前最受欢迎的数学数据集GSM8K和MATH,每个数据集的训练样本数量仅为约7.5K。为了解决这一挑战,研究者们尝试使用先进的LLMs(如GPT-3.5和GPT-4)来扩充现有的高质量数学数据集,但这些方法生成的新例子与原始训练集中的例子相似度过高,限制了它们在生成大规模数学数据集方面的能力。
论文标题:
MathScale: Scaling Instruction Tuning for Mathematical Reasoning
论文链接:
https://arxiv.org/pdf/2403.02884.pdf
论文概览:MathScale方法与MWPBENCH评测
1. MathScale方法
本文提出了一种名为MathScale的概念简单且可扩展的方法,它通过利用前沿LLMs(例如GPT-3.5)来创建高质量的数学推理数据。
MathScale的灵感来源于人类数学学习中的认知机制,首先从种子数学问题中提取主题和知识点,然后构建概念图,该图被用来生成新的数学问题。MathScale在研究者生成的数学数据集的规模方面展现出有效的可扩展性。结果,研究者创建了一个包含两百万个数学问题-答案对的数学推理数据集(MathScaleQA)。
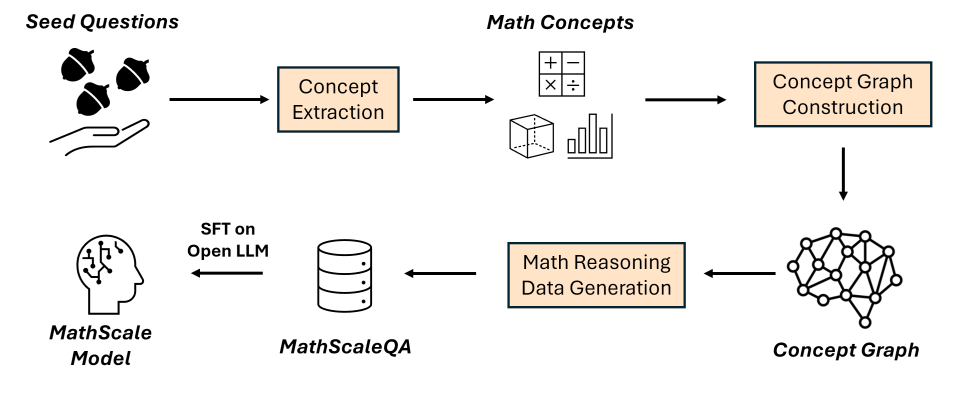
▲图为MathScale概述图
2. MWPBENCH评测
为了全面评估LLMs的数学推理能力,研究者构建了MWPBENCH,这是一个包含十个数据集(包括GSM8K和MATH)的数学文字问题(Math Word Problems)基准测试集,涵盖了从小学到大学以及竞赛级别的数学问题。
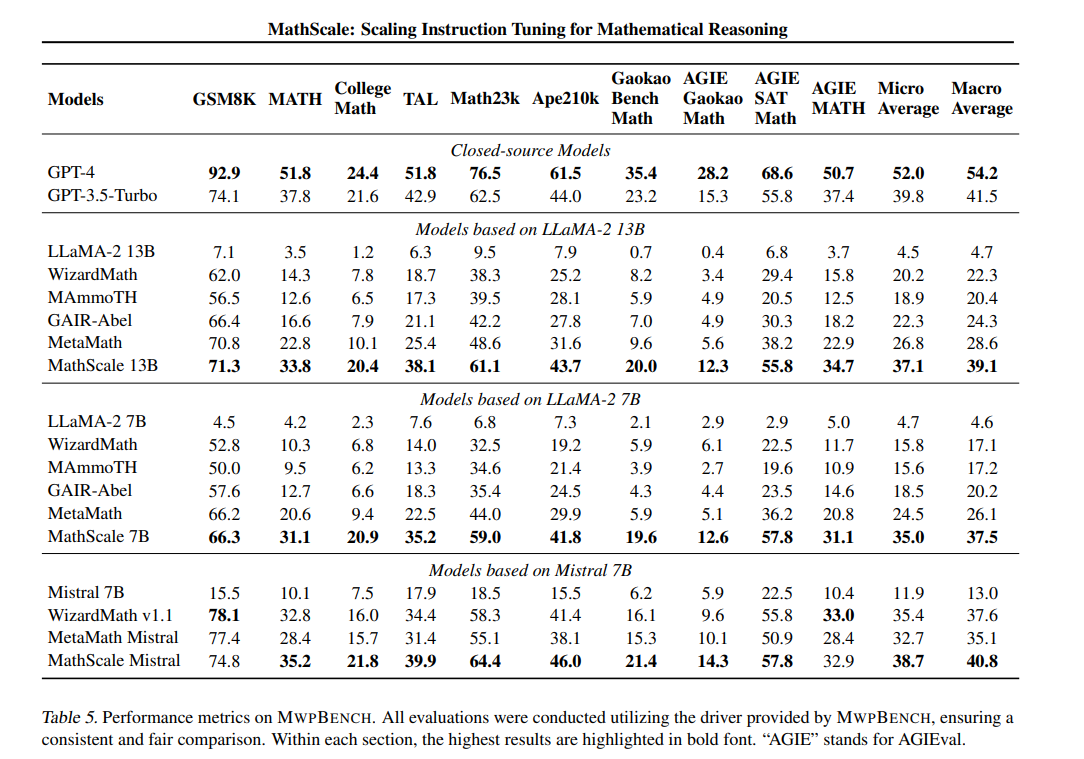
使用MathScaleQA对开源LLMs(例如LLaMA-2和Mistral)进行微调,显著提高了它们在数学推理方面的能力。在MWPBENCH上的评估显示,MathScale-7B在所有数据集上都取得了最先进的性能,相比同等规模的最佳对手,在微观平均准确率上提高了42.9%,在宏观平均准确率上提高了43.7%。
MathScale方法介绍
1. 概念提取:从种子数学问题中提取主题和知识点
MathScale方法首先从种子数学问题中提取高层次的概念,即主题和知识点。这一步骤通过对GPT-3.5进行提示工程来完成,旨在提取解决特定数学问题所需的元信息。
-
主题(topics)指的是数学科目名称或数学书章节的主题名称,如“金钱与金融”或“算术运算”。
-
知识点(knowledge points)则指问题解决中更细致的数学概念,例如“点积的定义和性质”或“将分数转换为整数”。
通过指导GPT-3.5扮演数学教师的角色,从给定的种子问题中提取1到2个主题和1到5个知识点。
2. 概念图构建:建立不同概念间的联系
在提取了主题和知识点之后,MathScale方法构建概念图,其节点为提取的主题和知识点。概念图中包含三种类型的边:主题到主题的边、主题到知识点的边以及知识点到知识点的边,从而形成三个子图(主题图、主题-知识点图、知识点图)。
当一个主题或知识点与另一个主题或知识点共同出现时,就在它们之间建立一条边,边的权重与它们的共现统计数据有关。这样,两个知识点(或主题)如果经常被用来解决相同的种子问题,它们就更有可能是合理的组合。
3. 数学推理数据生成:基于概念图生成新的数学问题
最后,MathScale方法使用概念图中的主题和知识点来生成新的数学问题。通过图随机游走算法来创建概念组合,从而用于生成新的数学问题。
-
首先从提取的主题中均匀随机抽样,然后在主题子图中随机游走一到两步以搜索相关主题。
-
接着在混合主题-知识点图中随机游走一步,以得到一个抽样的知识点。
-
最终,基于这些抽样的主题和知识点,指导GPT-3.5生成相应的数学问题和答案对。
在生成问题时,还包括了去污染过程,即从测试集中移除所有数学问题,以确保数据的质量。

MWPBENCH:全面的数学问题评测基准
1. 现有数据集的整合
MWPBENCH的构建首先从整合现有的数学问题数据集开始。
-
这些数据集包括GSM8K、MATH、TAL-SCQ、Math23k、Ape210k、GaokaoBench-Math以及AGIEval系列等。
这些数据集涵盖了从小学到大学,甚至竞赛级别的各种数学问题。为了统一评估标准,将原本的多项选择题转换为数学文字题目,并将非英语数据集翻译成英语,以确保评估的一致性。
2. CollegeMath数据集的构建
为了填补现有数据集中缺乏大学级别数学问题的空白,MWPBENCH引入了CollegeMath数据集。
-
该数据集从九本涵盖不同数学主题的大学教材中提取题目和答案,覆盖了代数、预微积分、微积分、向量微积分、概率、线性代数和微分方程等关键数学学科。

通过使用Mathpix API将PDF格式的教材转换为文本格式,并将其中的数学公式转换为LaTeX格式,从而提取出训练和测试用的题目。
3. 统一的评估协议
MWPBENCH采用统一的评估协议,以确保对不同模型的评估是公正和一致的。评估时采用零样本设置,并使用准确率作为评估指标。此外,还采用了Alpaca模板作为默认的提示模板,并选择贪婪解码以消除比较中的随机性。为了进一步规范化评估,实施了精确的答案提取和验证流程。
实验结果与分析
1. MathScale模型在MWPBENCH上的表现
MathScale-7B在MWPBENCH上的表现达到了最佳,无论是在微观平均准确率还是宏观平均准确率上,都超过了同等规模的最佳模型,分别提高了42.9%和43.7%。这证明了MathScaleQA数据集的有效性,以及通过该数据集微调开源大语言模型(如LLaMA-2和Mistral)所带来的显著改善。
2. MathScale的扩展性质
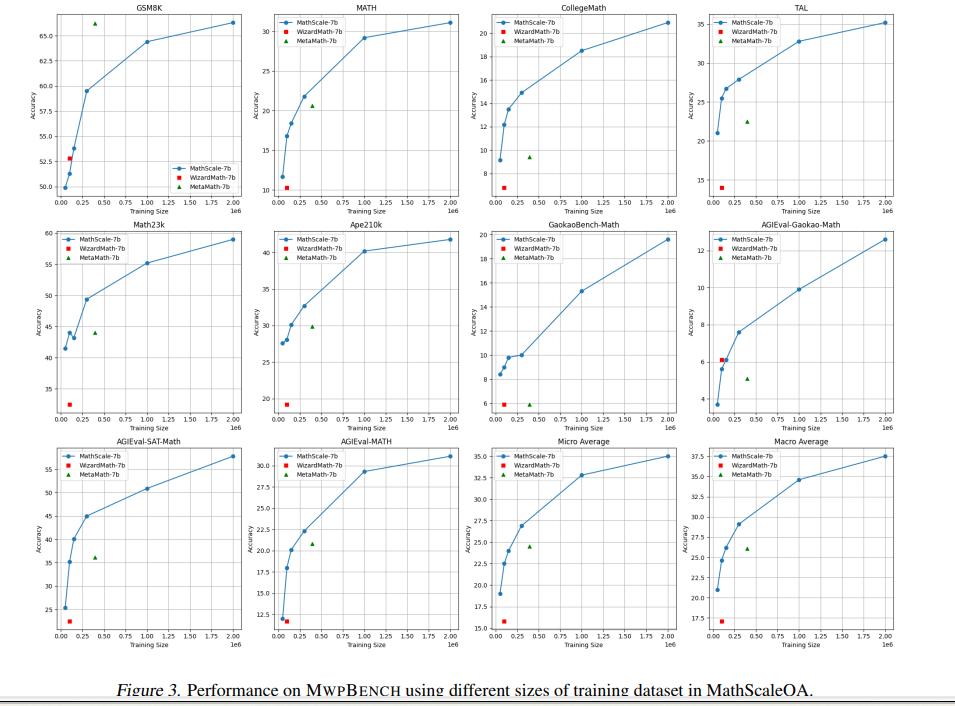
MathScale展示了在数学数据集规模方面的有效扩展性。通过迭代概念图来生成不同的数学概念组合,从而合成大量新的数学数据。实验结果表明,当扩大MathScaleQA数据集的规模时,MathScale-7B模型的性能呈现出近似对数增长的趋势。
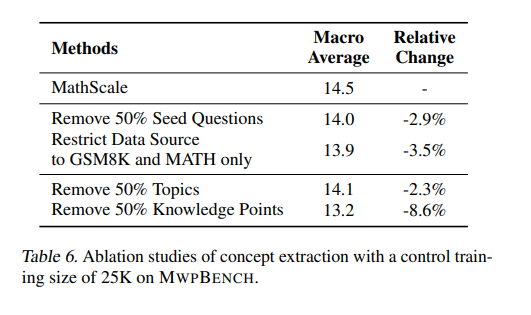
3. 概念提取的影响分析
在概念提取过程中,使用了MWPBENCH训练集中的约20K个种子问题。实验发现,更多和更多样化的种子问题有助于提升性能。此外,去除一半的知识点或主题会导致在MWPBENCH上的宏观平均准确率显著下降,尤其是知识点的减少对性能的影响更大。

4. 验证生成数据的有效性
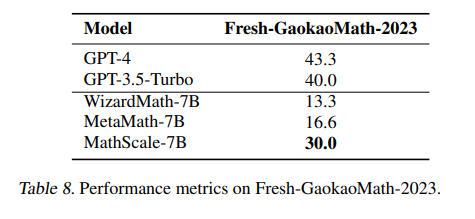
虽然MathScaleQA中生成的问答对可能存在错误,但在最终的MathScale流程中省略了额外的验证步骤,因为实验表明,验证步骤并没有提高结果。这可能是因为即使某些解决方案不正确,它们仍然有助于开源大语言模型学习GPT-3.5的分布。此外,MathScale在新鲜的数学数据集Fresh-GaokaoMath-2023上的表现也证明了其鲁棒性和适应性。
相关工作:ChatGPT在数学指导调整中的应用
1. ChatGPT的指导调整
在数学指导调整的进步中,使用ChatGPT进行数据合成是一个关键方面。例如,WizardMath引入了强化的evol-instruct,它整合了五种操作:增加约束、深化、具体化、增加推理步骤和复杂化输入,从而促进了全面的进化。
同样,MetaMath采用了一种引导问题的自举策略,包括答案增强、问题改述、自我验证和FOBAR问题。虽然这些方法有效,但它们的呼吸空间本质上受限于手动设计的操作。研究者的方法旨在使ChatGPT模仿人类数学学习中的认知过程,从而克服以前方法的局限性。
2. 工具集成的指导调整
最近的研究还探索了将工具集成到基于ChatGPT的数学指导调整中。ToRA结合了自然语言推理和基于程序的工具使用,以合成轨迹数据。每个轨迹迭代地连接推理、编程和程序输出,直到达到最终答案。目前的重点仅限于自然语言推理。虽然将工具集成到MathScale管道中是一个有趣的前景,但仍旧保留其未来研究的探索。
结论与展望
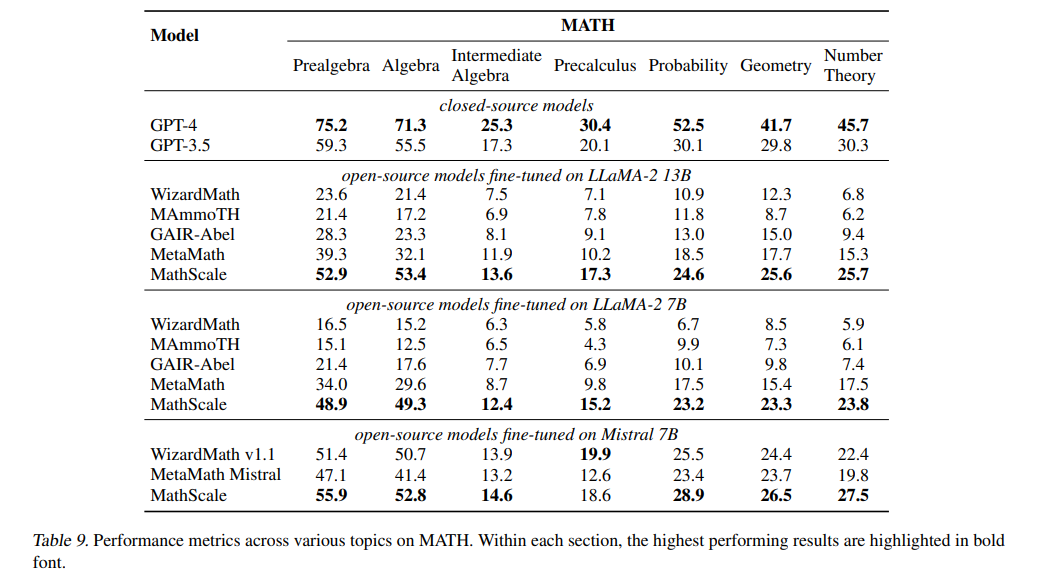
尽管本研究取得了显著的进展,但研究者们也认识到,LLMs在数学推理方面的能力仍有待进一步提升。例如,在微分方程的测试集上,所有模型都显示出有限的成功。此外,模型可能存在未在本研究中检验的偏见,这强调了需要进行全面评估的必要性,不仅要考虑技术性能,还要考虑模型与社会价值观的一致性。
展望未来,研究者预计MathScale的性能将随着更多合成训练示例的增加而继续提高。由于资源限制,研究者将训练集规模扩展到超过两百万示例的工作留待未来研究。






(+专栏数据结构练习是完整版))

)







)




