摘要：针对传统门锁钥匙易丢失、配置不便和忘记携带等问题，提出了一种基于STC89C52 的IC 卡门禁系统设计。该系统以STC89C52 单片机为核心来控制电子锁模块的开关。主要过程是由RFID 模块读取IC卡ID 并通过串口发送至STC89C52 单片机模块，STC89C52 单片机模块可以实现在线对IC 卡的ID 进行注册、删除和保存。当忘记带IC 卡时，可以通过按键模块输入密码，STC89C52 单片机模块可以实现对输入密码的修改和保存。实验结果表明：该系统可以有效解决传统门锁钥匙易丢失、配置不便和忘记携带以后的开锁问题。
关键词：单片机；在线注册；门禁

1 概述

传统门锁在钥匙丢失或忘记携带时，只能从窗户进入或者采取破坏门锁的办法开锁。传统门锁在配置时需要找专业人士，比较麻烦而且不能保证所配钥匙的准确性。在出租房屋业务中，由于经常换租客，传统门锁因为可以随意复制，安全系数低。针对这些问题提出了一种基于单片机的IC卡门禁系统[2]。IC卡门禁系统可以通过刷卡和输入密码两种方式开锁也可以随意更改密码，可以有效解决以上问题。

2 IC 卡门禁系统设计方案

IC卡门禁系统设计方案如图1系统设计方案图所示。

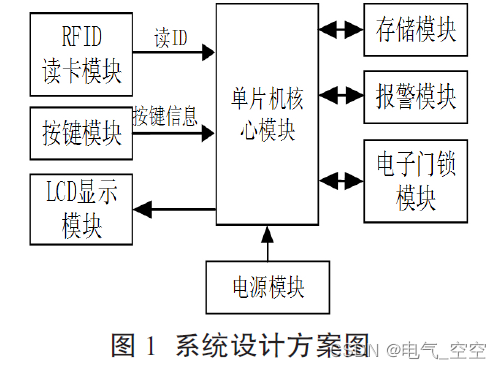
该系统由单片机核心模块、RFID读卡模块、LCD显示模块、电源模块、报警模块、电子门锁模块和存储模块七部分组成。系统的工作模式有设置模式和正常模式两种。系统上电后，按键模块若有设置按键按下，则系统进入设置模式。设置模式又分为更新密码和注册IC卡两种模式。设置模式完成以后，将信息存入存储模块。系统上电后，若按键模块设