1、标量(Scalar)
纯数字,无方向性、无维度概念。因此也叫 标量张量、零维张量、0D张量
例如,x1=8,x2=1.34
x1、x2即为标量
2、张量(tensor)
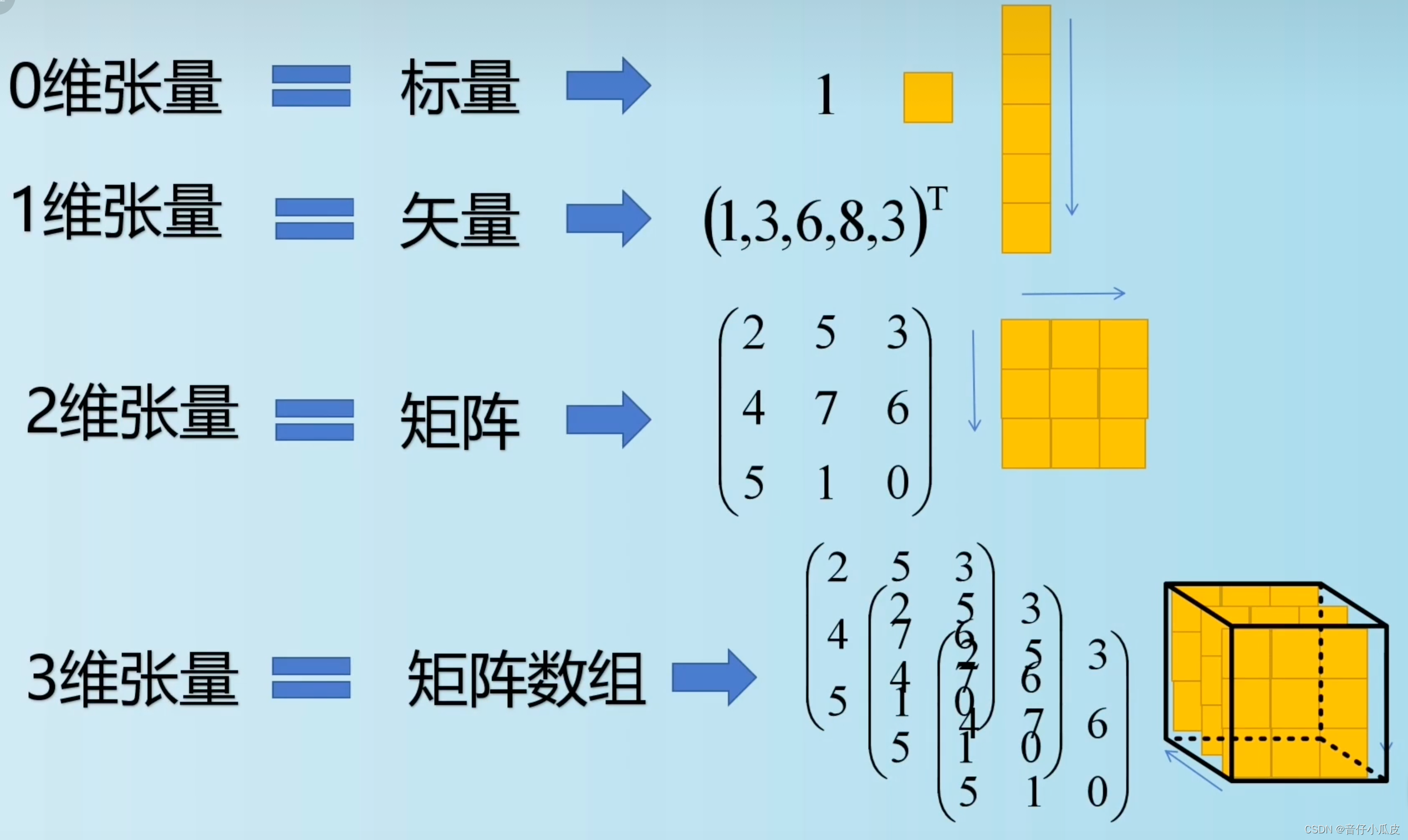
具有方向性,可以理解为一个多维数组,它是标量、向量、矩阵的高维扩展,属于一个数据容器。理论上,张量是向量概念上的推广,可以理解为其在多个维度的扩展。
通常,张量的维度被称作轴(axis),张量轴的个数也叫做阶(rank)
*张量由三个概念定义:
- 轴的个数(阶)
- 形状(shape):为一个整数元组,表示张量沿每个轴的维度大小(元素个数)。
- 数据类型(dtype):这是整个张量中数据元素的数据类型,张量的类型可以是 float32 、 uint8 、 float64 等。
3、向量(vector)
概念上为又代表方向,又代表大小的一组数,几何意义上对应一个点在坐标系上相对于原点的箭头指向。python形式上可以表现为数字组成的数组。向量又被称作一维张量(1D张量)。向量只有一个轴
例如,x=np.array([1,2,3,4])
x为一个向量
但是注意,上述x为4D向量,但不是4D张量!因为向量只有一个轴,只是在轴上有4个元素组成了4个维度!!
4、矩阵
矩阵属于二阶张量,在形式上可以表现为二维数组。
例如,x=np.array([[5, 78, 2, 34, 0], [6, 79, 3, 35, 1], [7, 80, 4, 36, 2]])
x属于矩阵
而三阶张量,相当于有3个轴,即由多个矩阵合成的一个新数组,例如:
np.array([[[5, 78, 2, 34, 0], [6, 79, 3, 35, 1], [7, 80, 4, 36, 2]], [[5, 78, 2, 34, 0], [6, 79, 3, 35, 1], [7, 80, 4, 36, 2]], [[5, 78, 2, 34, 0], [6, 79, 3, 35, 1], [7, 80, 4, 36, 2]]])








-全自动安装linux系统)


)

)
)
)

![[HackMyVm] Quick](http://pic.xiahunao.cn/[HackMyVm] Quick)

