前向与反向

---

• 这里我们从 一次计算 开始比如 z=f(x,y) 讨论
• 若我们把任意对于tensor的计算都看为函数（如将 a*b（数值） 看为 mul(a,b)），那么都可以将其看为2个过程：forward-前向，backward-反向
• 在pytorch中我们通过继承torch.autograd.Function来实现这2个过程，详细的用法和扩展参考：https://pytorch.org/docs/stable/notes/extending.html
• 【例子】比如我们要实现一个数值乘法z=$(x\ast y{)}^2$

前向

• 在前向过程中，我们主要干的事情为：1. 通过输入计算得到输出。2.保存反向传播求导数所需要的tensor到ctx（在反向传播的时候会对应的传入）
• 【例子】1.为了反向传播求梯度保存x，y（因为我们知道$dz/dx=2\ast x\ast y^2,dz/dy=2\ast y\ast x^2$）, 2.return $(x\ast y{)}^2$

反向

• 在反向传播的时候我们干的事情就是，将传入的导数（梯度）和我们在前向过程中保存的tensor进行加工，最终返回每个输入变量的梯度
• 【例子】此时反向时应该返回$2\ast x\ast x\ast y与2\ast x\ast y\ast y$，分别对应$dz/dx,dz/dy$

计算图

---

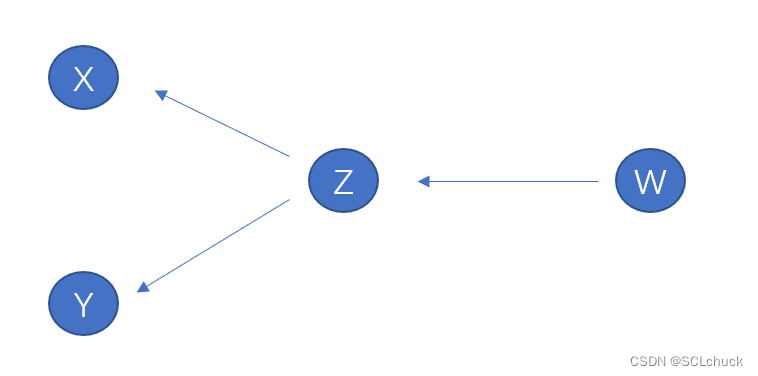
• 那么对于一次计算的讨论完了，现在我们来讨论多次计算，即梯度（导数）是如何一步步的从最终的z=f(a), a=g(b), b=w©… 一层层的 传回x的。
• 那么在pytorch中，其使用了图的数据结构，在一开始$z=x\ast x\ast y\ast y$的例子中，z会指向x与y，方便反向传播求梯度（导数），现在若$w=z\ast z$（关于z的函数），那么w会指向z
• 那么$dw/dx=dw/dz\ast dz/dx$
• 

需要梯度？，require_grad

• 但是很多tensor在计算时是不需要梯度的，而保存上面那种梯度图又很费空间，pytroch默认你创建的tensor是不需要梯度的
• 如当你使用线性层时，实际上是$w\ast x+b$，但是其实这里传入x是需要梯度的（它又不需要学习），而w与b是模型的参数是nn.Parameters，所以他需要学习，自然需要梯度，
• 而这里pytorch就使用一个bool标记来说明这个tensor需要梯度嘛，若他需要梯度，那么基于他的计算才会有指针指向它
• 比如，$z=x\ast y$，若x，y都require_grad=False,则根本不会建立计算图，若x的requires_grad=True,则该计算会建立z->x的计算图

梯度函数，grad_fn

• 当你进行了建立了计算图的计算，比如x.requires_grad=True, $z=x\ast y$, 那么z.grad_fn就会有函数指针指向反向传播的计算，这里就是这个$x\ast y$
• 在上图中一个节点虽然向回指向多个变量，但其实对应函数指针，其实是指向一个函数$x\ast x\ast y\ast y$，2个箭头对应的是2个返回值$(dz/dx,dz/dy)$，函数指针可以在运算完了后在tensor.grad_fn看到

梯度，grad

• 当你在正向计算时，构建完了上述的这样一个计算图，你就可以对最终得到的tensor调用backward函数，那么整个计算图就会从最后一个变量还是反向一步一步的将梯度传给每个需要保存梯度的tensor，这时可以在tensor.grad中看到，此时默认情况tensor.grad_fn会被清空。

torch.autograd.grad

---

• 大部分情况下，我们都是得到loss，然后loss.backward()，模型的参数对应的每个tensor就会的到梯度，这个时候opt.step()就会根据学习率优化参数
• 但有时候我们需要手动求导，可以使用 torch.autograd.grad函数

自变量，input

• x，即对什么求导，当然该tensor必须requires_grad=True，在因变量的同一梯度图的后继

因变量，output

• y，即被求导的变量，这里结合x相当于求dy/dx

加权，grad_outputs

• pytorch中求导的因变量必须是一个shape为[1]的tensor，所以比如当backward时，我们往往取loss.sum() 或者mean(), 那么这里y是个大小不定的tensor，那么这个参数就是和y的shape一样，先令（g代表grad_outputs）$L=\sum g_{ij}\ast y_{ij}$, 然后L在对x求导，这里求和往往我们取g=torch.ones_like(y), 相当于y.sum()
• 一般情况下，不同batch之间的计算是独立的，所以得到的y就算sum后，每个x的得到的梯度其实是batch独立的，但是batch_norm除外，因为batch_norm，不同batch的x会与整个batch的均值做运算， 除非你手写batch_norm，并将数据均值对应的tensor mu detach掉，此时mu对于整个梯度图就是一个常数，否则mu会指向不同batch的x，导致每个x的得到的梯度其实不是batch独立的

输出

• 输出的shape和x一样，即最终的L对于x每个位置的梯度，这也同样解释了为什么必须要对y求和得L，否则每个x中的每个位置其实对应整个tensor，y

二阶求导，create_graph

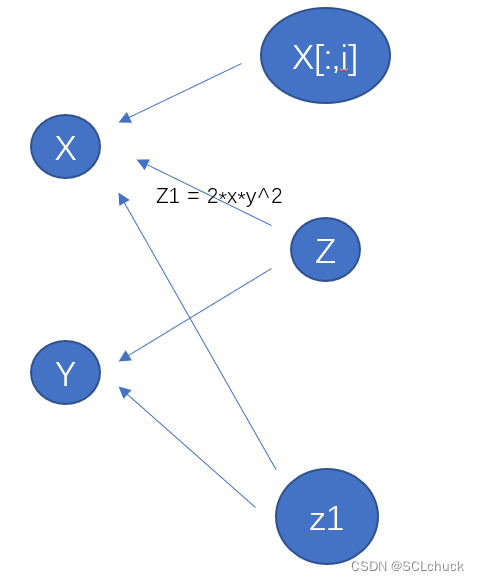
• 那么若想二阶求导，我们举个例子z = f(x,y) , z1 = ∂f/∂x， z2 = ∂z1 / ∂y，在代码里，其实x对应X[:,0], y对应X[:,1]（也可以其他对应）,其实还是一个tensor
• 那么首先把torch.autograd.grad整个过程又看为一次新的计算，在反向求导求z1时，程序会按照上述过程一步一步反向传播，而反向传播得到梯度时，其实这里又可以形成新的梯度图，z1处于整个新的梯度图顶端
• 那么对应代码里，使用函数参数create_graph=True来告诉autograd，我这次得到的tensor是需要产生梯度图的（因为可能进一步求导）
• 那么在代码里，我们相当于

 z1 = torch.autograd.grad(output=y,input=X,...)[0][:, 0]z2 = torch.autograd.grad(output=z1,input=X,...)[0][:, 1]若你的输入X是将x与y合成一体的，如x=X[:,0], y=X[:,1],那么你求导也只能将整体X作为输入，再从答案中获得对应的列
若你直接在求导时input=X[:,i] 这里实际上你创建了一个新tensor X[:,i] -> X, 而Z->X, 并未指向X[:,i], 故不行

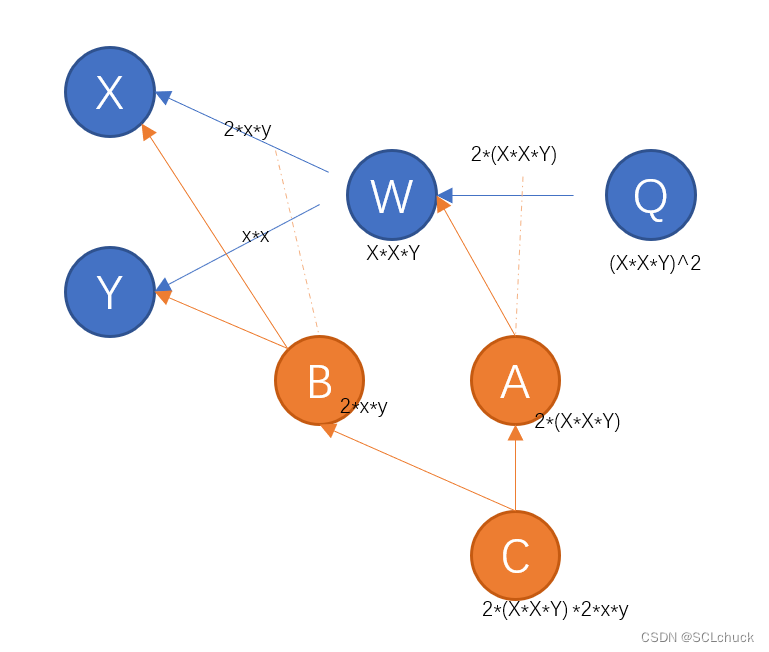
• 补充： 画2阶导数的梯度图

将一阶导数的梯度图的每一条边作为新的一个节点，例如s-[q]-> e, q作为一个新节点指向e，然后与其他同样从边引申出来的节点进行相乘链接（导数链式法则）一下是$Q=(x\ast x\ast y{)}^2$的例子