目录

1 主要内容

目标函数：

约束条件：

程序亮点总结：

2 代码问题与程序测试

设备出力运行结果：

3 下载链接 

---

1 主要内容

本程序是对《考虑源荷两侧不确定性的含风电电力系统低碳调度》的方法复现，主要实现了基于模糊机会约束的源荷两侧不确定性对含风电电力系统低碳调度的影响，将源荷不确定性采用清晰等价类进行处理，最终采用matlab+cplex进行求解。

目标函数：

约束条件：

功率平衡约束

新能源出力约束

常规水电机组约束

火电机组出力、爬坡、最小启停时间约束

储能约束

旋转备用约束

程序亮点总结：

1. 非线性处理，很显然，火电机组成本目标函数里含有两个非线性项：分别是平方项和两个布尔变量乘积，但是源程序这里还是存在问题的，详细看第二节程序运行对比。
2. 火电机组最小启停时间约束，这个程序理解可以看文末视频。

2 代码问题与程序测试

该程序代码为本人早期编写，代码弱点也很清楚，经过n次打磨，现可以就这部分问题进行分享，一是线性化处理的部分缺少一个约束，导致线性化处理不等价，存在严重偏差。

平方项分段线性化代码如下：

%分段线性化
gn=5;
gl1=(Pgmax-Pgmin)./gn;
gl2=zeros(5,gn+1);
for i=1:5
gl2(i,:)=Pgmin(i):gl1(i):Pgmax(i);
end
​
cons = [cons, x_pf(1,:)==gl2(1,:).^2*gw1];
cons = [cons, x_pf(2,:)==gl2(2,:).^2*gw2];
cons = [cons, x_pf(3,:)==gl2(3,:).^2*gw3];
cons = [cons, x_pf(4,:)==gl2(4,:).^2*gw4];
cons = [cons, x_pf(5,:)==gl2(5,:).^2*gw5];
cons = [cons, gw1(1,:)<=gz1(1,:)];
for i=2:gncons = [cons, gw1(i,:)<=gz1(i-1,:)+gz1(i,:)];
end
cons = [cons, gw1(gn+1,:)<=gz1(gn,:)];
cons = [cons, sum(gz1)==ones(1,Horizon)];
cons = [cons, gw2(1,:)<=gz2(1,:)];
for i=2:gncons = [cons, gw2(i,:)<=gz2(i-1,:)+gz2(i,:)];
end
cons = [cons, gw2(gn+1,:)<=gz2(gn,:)];
cons = [cons, sum(gz2)==ones(1,Horizon)];
cons = [cons, gw3(1,:)<=gz3(1,:)];
for i=2:gncons = [cons, gw3(i,:)<=gz3(i-1,:)+gz3(i,:)];
end
cons = [cons, gw3(gn+1,:)<=gz3(gn,:)];
cons = [cons, sum(gz3)==ones(1,Horizon)];
cons = [cons, gw4(1,:)<=gz4(1,:)];
for i=2:gncons = [cons, gw4(i,:)<=gz4(i-1,:)+gz4(i,:)];
end
cons = [cons, gw4(gn+1,:)<=gz4(gn,:)];
cons = [cons, sum(gz4)==ones(1,Horizon)];
cons = [cons, gw5(1,:)<=gz5(1,:)];
for i=2:gncons = [cons, gw5(i,:)<=gz5(i-1,:)+gz5(i,:)];
end
cons = [cons, gw5(gn+1,:)<=gz5(gn,:)];
cons = [cons, sum(gz5)==ones(1,Horizon)];
cons = [cons, PG(1,:)==gl2(1,:)*gw1];
cons = [cons, PG(2,:)==gl2(2,:)*gw2];
cons = [cons, PG(3,:)==gl2(3,:)*gw3];
cons = [cons, PG(4,:)==gl2(4,:)*gw4];
cons = [cons, PG(5,:)==gl2(5,:)*gw5];

平方线性化的理论很简单，分段采用直线代替曲线，很多文献都采用这种方法来处理，这段线性化约束中x_pf为PG的平方项变量，因为没有设定x_pf大于等于0的约束，导致程序结果出现严重错误，下图为截取的部分运行结果，优化结果中x_pf存在小于0的数值，这是严重不对的。

设备出力运行结果：

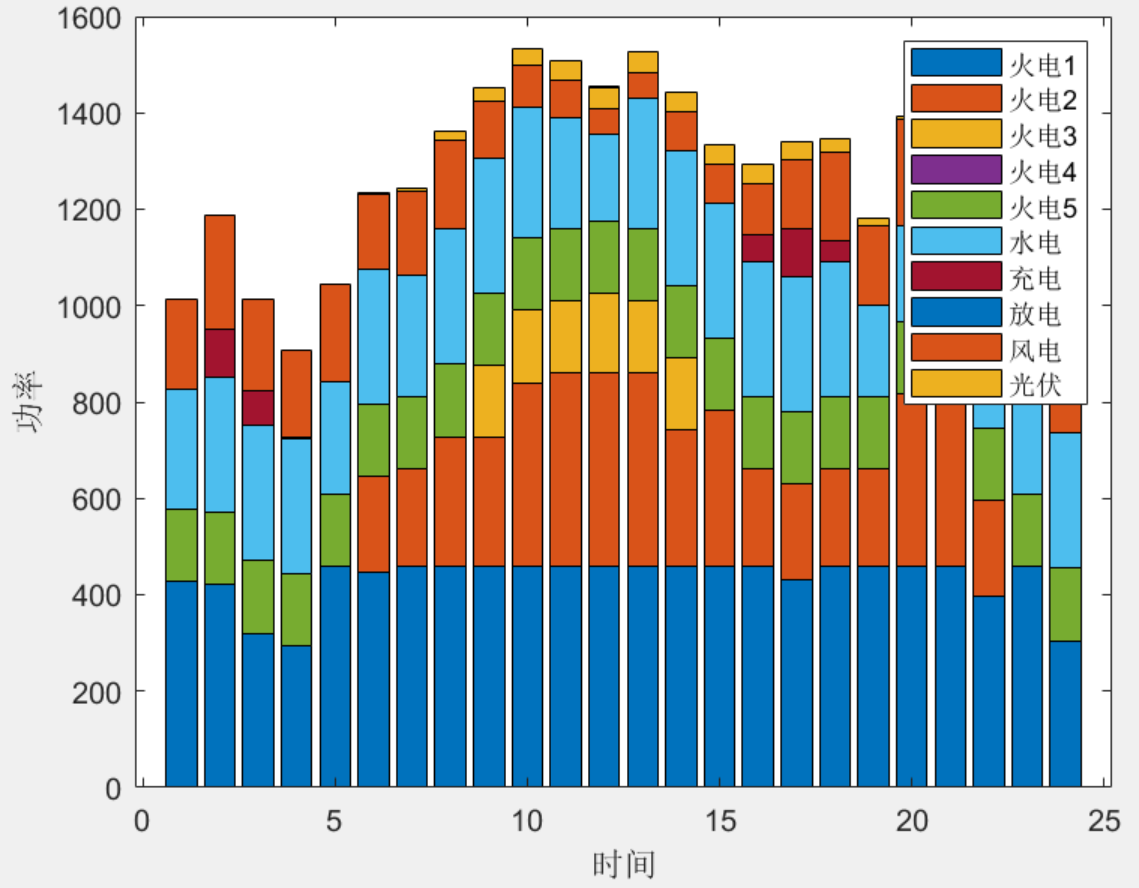
补充上x_pf大于等于0的约束后，x_pf就不会出现负值。将PG进行平方和x_pf进行对比看一下误差情况。

这是1个火电机组的优化结果对比，PG的平方远比其线性化后的平方值大，这和火电机组运行区间以及线性化的精细度相关，但是这种偏差会导致结果与预期差距大，并且找不出程序原因。

大家可以翻看一下【深度学习】模块的资料，里面有关于非线性的例子，我们采用直接非线性约束的方式进行优化，看一下优化结果。

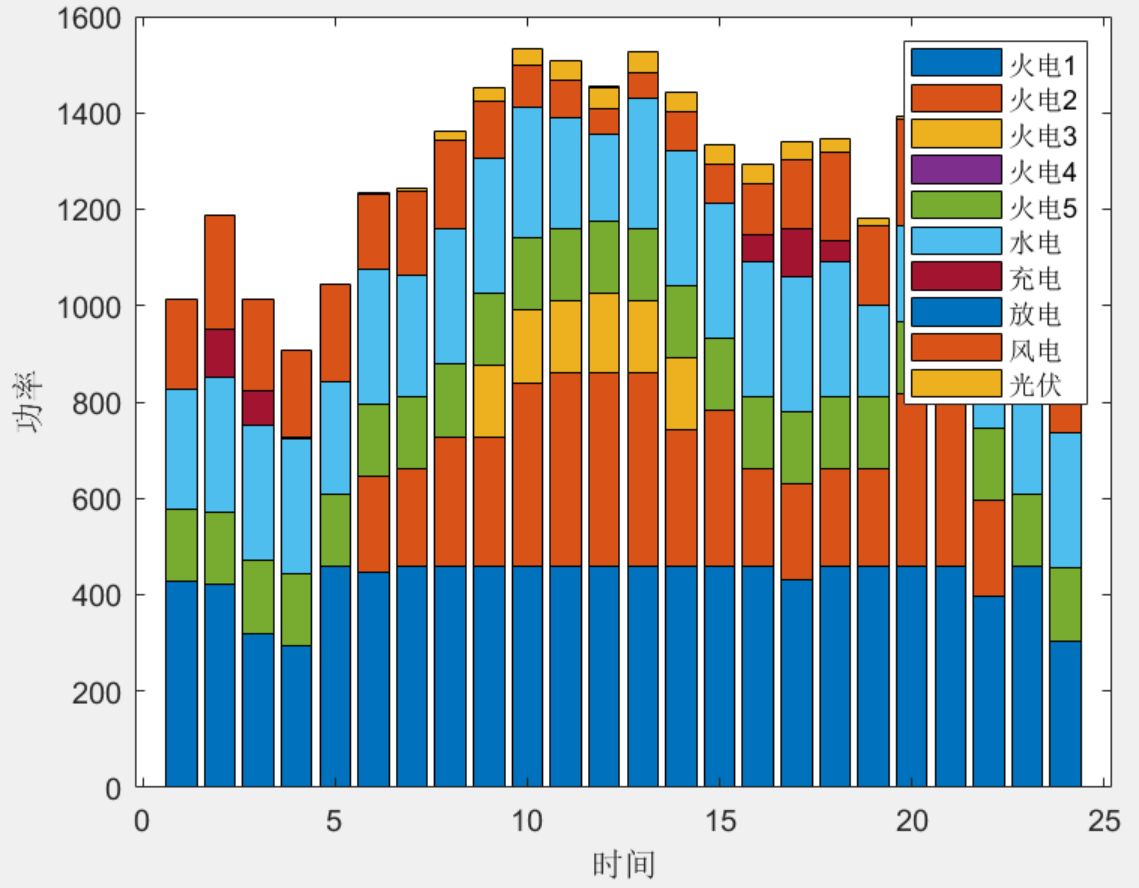
为了对比一下优化结果的差异性，见下面对比图。

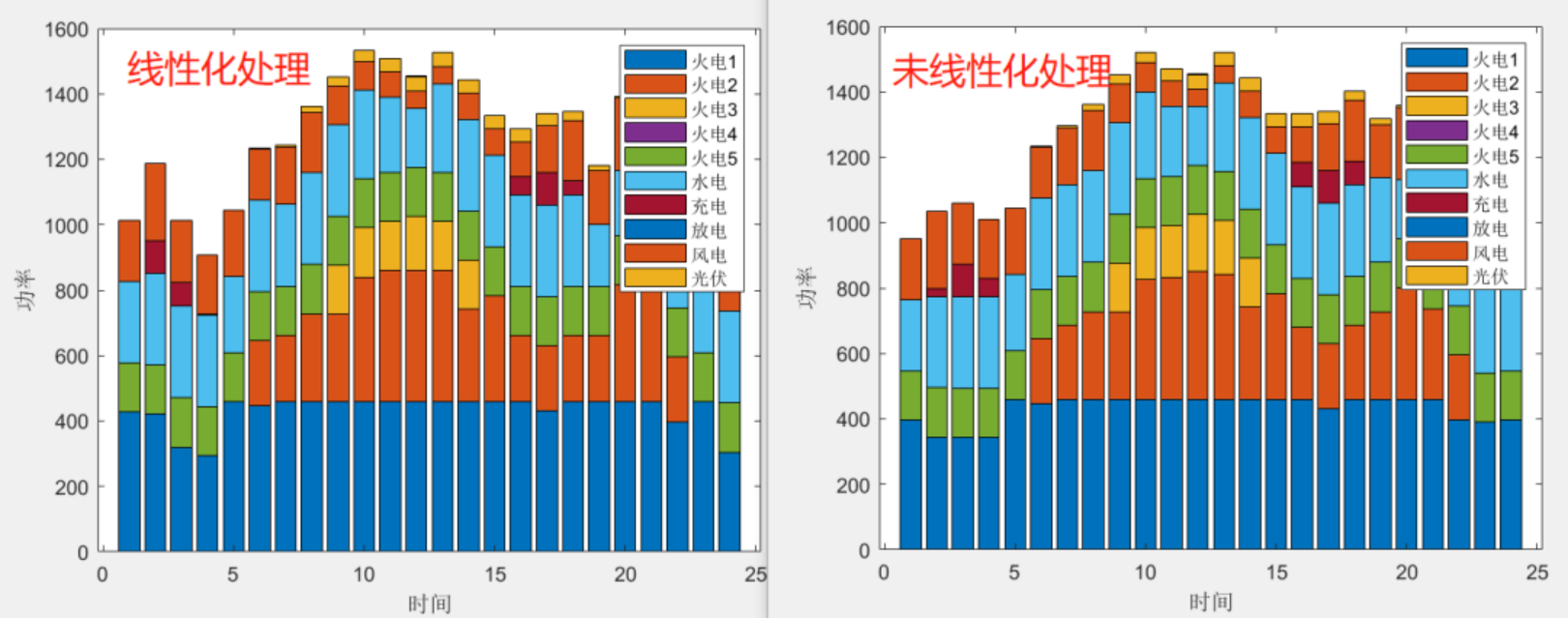
很明显存在较大差异，再来看一下平方项的对比图。

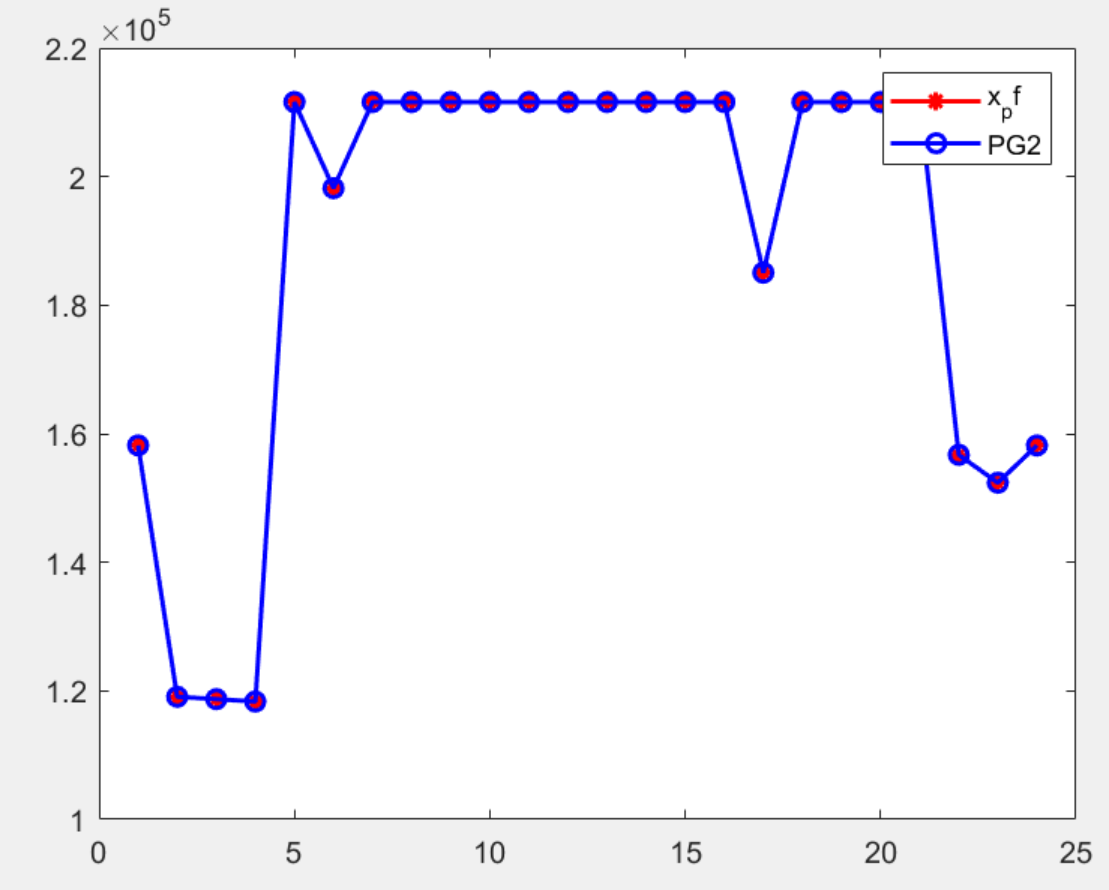
两条曲线完全重合，说明采用非线性化约束得到的结果没有问题，对于哪种情况下可以直接非线性约束哪种情况需要线性化，后期我专题分享一下这部分内容。

本次将线性化处理后的程序和非线性约束直接表达的程序一并打包，以供大家在学术过程中做个对比，方便大家不断探索和进步，下面贴出其他部分程序代码。

Pgmin=[230 200 150 120 70]';%火电机组功率下限
Pgmax=[460 400 350 300 150]';%火电机组功率上限
Phmin=0;%水电下限
Phmax=280;%水电上限
rud=[240 210 150 120 70]';%火电爬坡
On_min=[8 7 6 4 3]';%开机时间
Off_min=[8 7 6 4 3]';%关机时间
a=1e-5.*[1.02 1.21 2.17 3.42 6.63]';%火电机组表格数据，下同
b=[0.277 0.288 0.29 0.292 0.306]';
c=[9.2 8.8 7.2 5.2 3.5]';
Sit=[25.6 22.3 16.2 12.3 4.6]';
e=[0.877 0.877 0.877 0.877 0.979]';
lam=[0.94 0.94 0.94 0.94 1.03]';
%储能参数
capmax=400;
EESmax=100;
EESmin=0;
socmax=0.9;
socmin=0.2;
theta=0.01;%自放电率
yita=0.95;
%-------------
w=50;d=100;tao=0.25;%碳交易价格、区间长度、增长幅度
Horizon=24;%时间参数
ngen=5;%火电机组数量
%% 决策变量
PG = sdpvar(ngen, Horizon);%火电
PH = sdpvar(1, Horizon);%水电
x_P_ch = sdpvar(1, Horizon);%充电
x_P_dis = sdpvar(1, Horizon);%放电
x_P_w = sdpvar(1, Horizon);%风电
x_P_v = sdpvar(1, Horizon);%水电
x_u_ch = binvar(1, Horizon);%充电状态
x_u_dis = binvar(1, Horizon);%放电状态
OnOff = binvar(ngen,Horizon);%火电机组状态
lin = sdpvar(1, Horizon);%目标3中间变量
%P的平方线性化参数
gn=5;
x_pf=sdpvar(ngen, Horizon);
gw1=sdpvar(gn+1,Horizon);
gw2=sdpvar(gn+1,Horizon);
gw3=sdpvar(gn+1,Horizon);
gw4=sdpvar(gn+1,Horizon);
gw5=sdpvar(gn+1,Horizon);
gw6=sdpvar(gn+1,Horizon);
gz1=binvar(gn, Horizon);gz2=binvar(gn, Horizon);gz3=binvar(gn, Horizon);gz4=binvar(gn, Horizon);gz5=binvar(gn, Horizon);
%模型构建
%% 约束条件生成
cons = [];
%火电机组cons_gen = getConsGen1(PG,Pgmax,Pgmin,rud, Horizon,OnOff,On_min,Off_min);cons = [cons, cons_gen];
%水电机组
cons = [cons, repmat(Phmin,1,Horizon)<=PH<=repmat(Phmax,1,Horizon)];
%储能约束cons_ees = getConsEES(x_P_ch, x_P_dis, x_u_ch, x_u_dis, EESmax, EESmin, capmax, Horizon,theta);cons = [cons, cons_ees];
%新能源出力约束
cons = [cons,0 <= x_P_w <=pw, 0 <= x_P_v <=pv]; 

3 下载链接